Формула силы тяги в физике
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Содержание:
- Определение и формула силы тяги
- Единицы измерения силы тяги
- Примеры решения задач
В том случае, если тело при перемещении имеет ускорение, то на него кроме всех прочих обязательно действует некоторая сила, которая является силой тяги в рассматриваемый момент времени. В действительности, если тело движется прямолинейно и с постоянной скоростью, то сила тяги также действует, так как тело должно преодолевать силы сопротивления. Обычно силу тяги находят, рассматривая силы, действующие на тело, находя равнодействующую и применяя второй закон Ньютона. Жестко определенной формулы для силы тяги не существует.
Не следует считать, что сила тяги, например, транспортного средства действует со стороны двигателя, так как внутренние силы не могут менять
скорость системы как единого целого, что входило бы в противоречие с законом сохранения импульса.
$$P=\bar{F}_{T} \bar{v}(1)$$
Определение и формула силы тяги
Определение
Исходя из формулы (1) силу тяги можно определить через полезную мощность, и скорость транспортного средства (v):
$$F_{T}=\frac{P}{v}(2)$$
Для автомобиля, поднимающегося в горку, которая имеет уклон , масса автомобиля m сила тяги (F T) войдет в уравнение:
$$F_{T}-F_{s}-m g \sin \alpha=m a(3)$$
где a – ускорение, с которым движется автомобиль.
Единицы измерения силы тяги
Основной единицей измерения силы в системе СИ является: [FT]=Н
В СГС: [FT]=дин
Примеры решения задач
Пример
Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения, которая равна $\mu$=0,1 от силы тяжести. Какой будет сила тяги, если автомобиль движется с ускорением 2 м/с?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем второй закон Ньютона:
$$\bar{N}+m \bar{g}+\bar{F}_{t r}+\bar{F}_{T}=m \bar{a}(1.1)$$
Спроектируем уравнение (1.1) на оси X и Y:
$$ \begin{array}{c} X: F_{T}-F_{t r}=m a(1.2) \\ Y: m g=N(1.3) \end{array} $$
$$ F_{t r}=\mu \cdot m g (1.4) $$
Подставим правую часть выражения (1.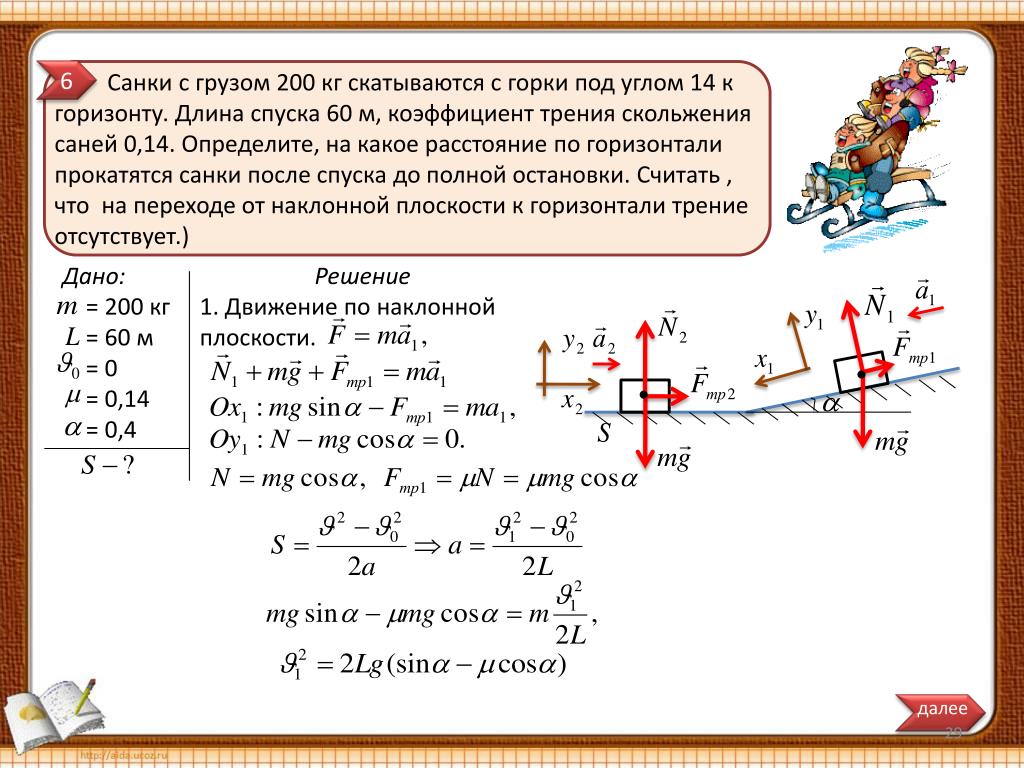 {3}(H)$$
{3}(H)$$
Ответ. FT=2,98 кН
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. На гладкой горизонтальной поверхности лежит доска массой M. На доске находится тело массы m. Коэффициент трения тела о доску равен $\mu$ . К доске приложена сила горизонтальная сила тяги, которая зависит от времени как: F=At (где A=const). В какой момент времени доска начнет выскальзывать из-под тела?
Решение. Сделаем рисунок.
Для решения задачи нам потребуются проекции сил на осиX и Y, которые отличны от нуля. Для тела массы m:
$$
\begin{array}{c}
X: m a_{1}=F_{t r}(2.1) \\
Y: m g=N(2.2) \\
F_{t r}=\mu N=\mu m g \rightarrow m a_{1}=\mu m g \rightarrow a_{1}=\mu g(2. 3)
\end{array}
$$
3)
\end{array}
$$
Для тела массы M:
$$M a_{2}=F-F_{t r} \rightarrow M a_{2}=A t-F_{t r} \rightarrow a_{2}=\frac{A t-F_{t r}}{M}(2.2)$$
Обозначим момент времени, в который доска начнет выскальзывать из-под тела t0, тогда
$$\mu g=\frac{A t_{0}-\mu m g}{M} \rightarrow t_{0}=\frac{m+M}{A} \mu g$$
Ответ. $t_{0}=\frac{m+M}{A} \mu g$
Читать дальше: Формула силы упругости.
Формула силы тяги — онлайн справочник для студентов
ОПРЕДЕЛЕНИЕ
Сила тяги при рассмотрении транспортных средств называется внешней силой, которая должна быть реализована с использованием машины или механизма для перемещения груза.
Сама по себе концепция «тяговой силы» имеет смысл только по отношению к любому транспортному средству, например, говорить о тяговой силе автомобиля, самолета, лошади, тянуть сани.
Единицей измерения силы является Н (Ньютон).
Очень заманчиво заключить, что источником тяги автомобиля является его двигатель. Однако это неверно. Внутренние силы одной части системы (двигателя), действующие на другую часть системы (колеса), не могут ускорить всю систему (весь автомобиль), так как это противоречит закону сохранения импульса. Источником тяги являются внешние воздействия. В случае с автомобилем это сила трения колес на поверхности дороги, в случае корабля — сила струи воды, выброшенной пропеллером.
Нет единой универсальной формулы для расчета силы тяги. Сила тяги определяется конструкцией транспортного средства и физическими условиями проблемы.
Примеры решения проблем по теме «Тяга»
ПРИМЕР 1
Автомобиль весом 4 тонны движется по ровной дороге с ускорением . Найдите силу тяги двигателя автомобиля, если коэффициент трения .
Мы делаем картину:
При движении по машине сила тяжести , сила реакции опоры , сила трения и тяговое усилие действуют. Под действием этих сил автомобиль движется с ускорением .
Под действием этих сил автомобиль движется с ускорением .
Согласно второму закону Ньютона:
Введем систему координат, как показано на рисунке, и запишем это векторное равенство в проекциях на оси координат.
Сила трения . Из второго уравнения . Поэтому мы можем написать ( . Замените значение силы трения в первом уравнении и определите силу тяги автомобильного двигателя:
Ускорение силы тяжести
Подставляя в формулу численные значения физических величин, вычисляем:
Двигатель двигателя тяги
ПРИМЕР 2
Автомобиль весом 4 тонны движется в гору с наклоном 1 м на каждые 25 м пути с постоянной скоростью. Найдите силу тяги двигателя автомобиля, если коэффициент трения
Мы делаем картину:
В этом примере, как и в предыдущем, при движении автомобиля сила тяжести , сила реакции поддержки , сила трения и тяговое усилие действуют на автомобиль. И под влиянием этих сил автомобиль движется в гору с постоянной скоростью, то есть ускорение автомобиля .
И под влиянием этих сил автомобиль движется в гору с постоянной скоростью, то есть ускорение автомобиля .
Согласно второму закону Ньютона:
Запишем это векторное равенство в проекциях на оси координат:
Из второго уравнения и силы трения .
Подставляя значение силы трения в первое уравнение, мы определяем силу тяги:
Из геометрии проблемы:
Наконец, сила тяги двигателя:
Усилие тяги автомобильного двигателя
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Длина волны Формула средней скорости Формула количества теплоты Формула силы упругости Формула силы натяжения нити
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
определение, формулы для вычисления и примеры из реальной жизни
Разберёмся в вопросе, что такое сила тяги. Как следует из самого названия – это сила, которую необходимо прикладывать к телу, чтобы оно находилось в состоянии постоянного движения.
Как следует из самого названия – это сила, которую необходимо прикладывать к телу, чтобы оно находилось в состоянии постоянного движения.
Если её убрать, то тело, будь то автомобиль, электровоз, космическая ракета или санки, со временем остановится. Это произойдёт потому, что на тело всегда действуют силы, которые заставляют его стремиться к состоянию покоя:
- силы трения (покоя, качения, скольжения),
- сопротивления воздуха (газа),
- сопротивления воды и др.
Содержание:
- Первый и второй законы Ньютона
- Примеры из жизни
- Насколько вы сильны?
- Насколько силён ваш автомобиль?
Первый и второй законы Ньютона
Обратимся к законам Ньютона, которые хорошо описывают механическое движение тел. Из школьной программы мы знаем, что есть первый закон Ньютона, который описывает закон инерции. Он гласит, что любое тело, если на него не действуют силы, или если их равнодействующая равна нулю, движется прямолинейно и равномерно, или же находится в состоянии покоя. Это означает, что тело, пока на него ничто не действует, будет двигаться с постоянной скоростью v=const или пребывать в состоянии покоя сколько угодно долго, пока какое-то внешнее воздействие не выведет тело из этого состояния. Это и есть движение по инерции.
Это означает, что тело, пока на него ничто не действует, будет двигаться с постоянной скоростью v=const или пребывать в состоянии покоя сколько угодно долго, пока какое-то внешнее воздействие не выведет тело из этого состояния. Это и есть движение по инерции.
Надо сказать, что этот закон справедлив лишь в так называемых инерциальных системах отсчёта. В неинерциальных системах отсчёта этот закон не действует и нужно использовать второй закон Ньютона. В таких системах отсчёта тело тоже будет двигаться по инерции, но оно будет двигаться с ускорением, стремясь сохранять своё движение, т.е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.
Этот закон утверждает, что для того, чтобы вывести тело из состояния покоя или равномерного движения, к нему необходимо приложить силу, равную F=m•a, где m — это масса тела, a — ускорение, сообщаемое телу.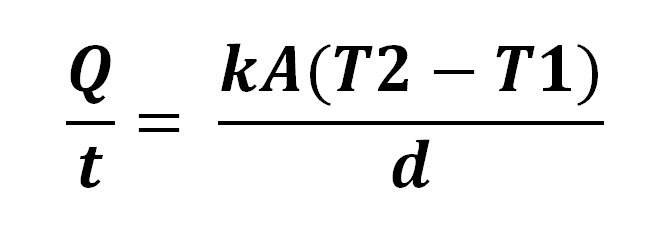 Зная эти законы, можно рассчитать силу тяги (двигателя автомобиля, ракетного двигателя или, например, лошади, тянущей нагруженную повозку).
Зная эти законы, можно рассчитать силу тяги (двигателя автомобиля, ракетного двигателя или, например, лошади, тянущей нагруженную повозку).
Примеры из жизни
Насколько вы сильны?
Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.
Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.
Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения.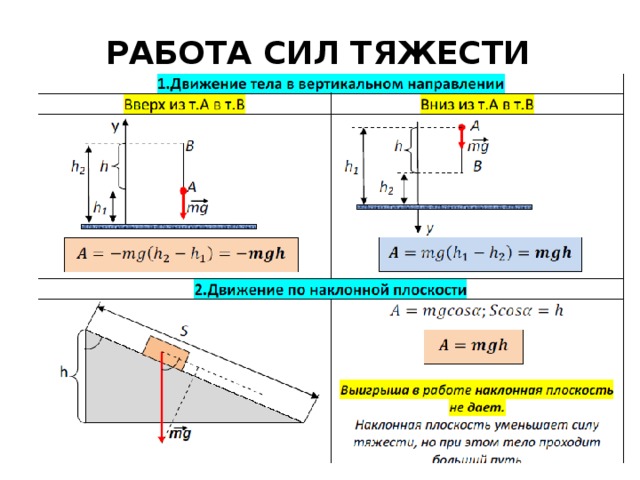 Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).
Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).
Насколько силён ваш автомобиль?
Рассмотрим ещё пример. У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
Допустим, вы разогнали свой автомобиль до скорости v за какое-то время t, проехав расстояние s. Тогда Fтяги будет легко рассчитана по формуле: Fтяги = m•v/t. Как и в примере с санками, справедлива также такая формула: Fтяги = f•m•g, где f – коэффициент трения качения, который зависит от скорости автомобиля (чем больше скорость, тем меньше этот коэффициент).
Но что делать, если масса автомобиля m, коэффициент трения качения f и время разгона t неизвестны ? Тогда можно поступить по-другому. Двигатель вашего автомобиля при разгоне совершил работу A = Fтяги • s. Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Двигатель вашего автомобиля при разгоне совершил работу A = Fтяги • s. Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Допустим, вы разогнали свой автомобиль до скорости v = 180 км/ч, а мощность его двигателя N = 200 л. с. (лошадиных сил). Чтобы вычислить Fтяги двигателя, необходимо прежде перевести указанные единицы измерения в единицы СИ, т. е. международной системы измерения. Здесь 1 л. с. = 735,499 Вт, поэтому мощность двигателя составит N = 200 л. с. • 735,499 Вт/л. с. = 147099,8 Вт. Скорость в системе СИ будет равна v = 180 км/ч = 180 • 1000 м/3600 с = 50 м/с. Тогда искомое значение будет равно Fтяги = 147099,8 Вт/50 (м/с) = 2941,996 Н ~ 2,94 кН (килоньютона).
Около 3 килоньютонов. Много это или мало ? Допустим, вы жмёте 100 килограммовую штангу. Чтобы её поднять, вам нужно преодолеть её вес, равный P = m•g = 100 кг • 9,81 м/с² = 981 Н (ньютон)~0,98 кН. Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Чтобы её поднять, вам нужно преодолеть её вес, равный P = m•g = 100 кг • 9,81 м/с² = 981 Н (ньютон)~0,98 кН. Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Таким образом, зная школьный курс физики, мы можем с лёгкостью вычислить силу тяги:
- человека,
- лошади,
- паровоза,
- автомобиля,
- космической ракеты и всех прочих видов техники.
Видео
В нашем видео вы найдете интересные опыты, поясняющие, что такое сила тяги и сила сопростивления.
Формула силы тяги при равномерном движении
Разберёмся в вопросе, что такое сила тяги. Как следует из самого названия – это сила, которую необходимо прикладывать к телу, чтобы оно находилось в состоянии постоянного движения.
Если её убрать, то тело, будь то автомобиль, электровоз, космическая ракета или санки, со временем остановится. Это произойдёт потому, что на тело всегда действуют силы, которые заставляют его стремиться к состоянию покоя:
- силы трения (покоя, качения, скольжения),
- сопротивления воздуха (газа),
- сопротивления воды и др.
Первый и второй законы Ньютона
Обратимся к законам Ньютона, которые хорошо описывают механическое движение тел. Из школьной программы мы знаем, что есть первый закон Ньютона, который описывает закон инерции. Он гласит, что любое тело, если на него не действуют силы, или если их равнодействующая равна нулю, движется прямолинейно и равномерно, или же находится в состоянии покоя. Это означает, что тело, пока на него ничто не действует, будет двигаться с постоянной скоростью v=const или пребывать в состоянии покоя сколько угодно долго, пока какое-то внешнее воздействие не выведет тело из этого состояния. Это и есть движение по инерции.
Это и есть движение по инерции.
Надо сказать, что этот закон справедлив лишь в так называемых инерциальных системах отсчёта. В неинерциальных системах отсчёта этот закон не действует и нужно использовать второй закон Ньютона. В таких системах отсчёта тело тоже будет двигаться по инерции, но оно будет двигаться с ускорением, стремясь сохранять своё движение, т.е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.
Этот закон утверждает, что для того, чтобы вывести тело из состояния покоя или равномерного движения, к нему необходимо приложить силу, равную F=m•a, где m — это масса тела, a — ускорение, сообщаемое телу. Зная эти законы, можно рассчитать силу тяги (двигателя автомобиля, ракетного двигателя или, например, лошади, тянущей нагруженную повозку).
Примеры из жизни
Насколько вы сильны?
Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.
Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.
Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).
Насколько силён ваш автомобиль?
Рассмотрим ещё пример. У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
Допустим, вы разогнали свой автомобиль до скорости v за какое-то время t, проехав расстояние s. Тогда Fтяги будет легко рассчитана по формуле: Fтяги = m•v/t. Как и в примере с санками, справедлива также такая формула: Fтяги = f•m•g, где f – коэффициент трения качения, который зависит от скорости автомобиля (чем больше скорость, тем меньше этот коэффициент).
Но что делать, если масса автомобиля m, коэффициент трения качения f и время разгона t неизвестны ? Тогда можно поступить по-другому. Двигатель вашего автомобиля при разгоне совершил работу A = Fтяги • s. Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Допустим, вы разогнали свой автомобиль до скорости v = 180 км/ч, а мощность его двигателя N = 200 л. с. (лошадиных сил). Чтобы вычислить Fтяги двигателя, необходимо прежде перевести указанные единицы измерения в единицы СИ, т. е. международной системы измерения. Здесь 1 л. с. = 735,499 Вт, поэтому мощность двигателя составит N = 200 л. с. • 735,499 Вт/л. с. = 147099,8 Вт. Скорость в системе СИ будет равна v = 180 км/ч = 180 • 1000 м/3600 с = 50 м/с. Тогда искомое значение будет равно Fтяги = 147099,8 Вт/50 (м/с) = 2941,996 Н
2,94 кН (килоньютона).
Около 3 килоньютонов. Много это или мало ? Допустим, вы жмёте 100 килограммовую штангу. Чтобы её поднять, вам нужно преодолеть её вес, равный P = m•g = 100 кг • 9,81 м/с² = 981 Н (ньютон)
0,98 кН. Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Таким образом, зная школьный курс физики, мы можем с лёгкостью вычислить силу тяги:
- человека,
- лошади,
- паровоза,
- автомобиля,
- космической ракеты и всех прочих видов техники.
В нашем видео вы найдете интересные опыты, поясняющие, что такое сила тяги и сила сопростивления.
Сила тяги при рассмотрении транспортных средств называется внешней силой, которая должна быть реализована с использованием машины или механизма для перемещения груза.
Сама по себе концепция «тяговой силы» имеет смысл только по отношению к любому транспортному средству, например, говорить о тяговой силе автомобиля, самолета, лошади, тянуть сани.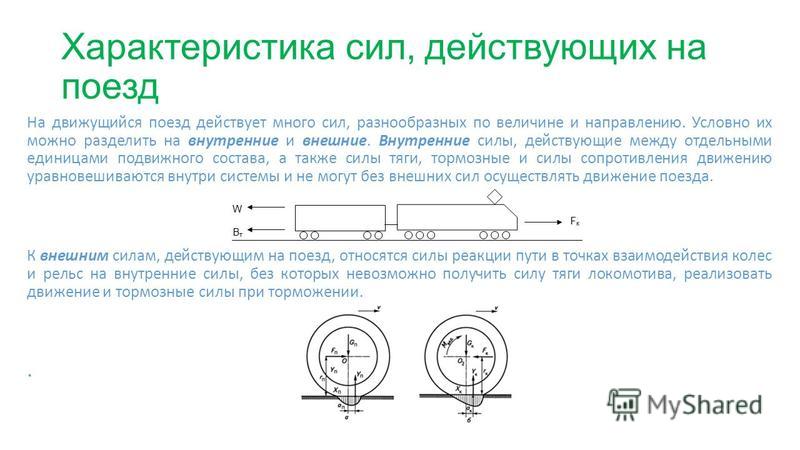
Единицей измерения силы является Н (Ньютон).
Очень заманчиво заключить, что источником тяги автомобиля является его двигатель. Однако это неверно. Внутренние силы одной части системы (двигателя), действующие на другую часть системы (колеса), не могут ускорить всю систему (весь автомобиль), так как это противоречит закону сохранения импульса. Источником тяги являются внешние воздействия. В случае с автомобилем это сила трения колес на поверхности дороги, в случае корабля – сила струи воды, выброшенной пропеллером.
Нет единой универсальной формулы для расчета силы тяги. Сила тяги определяется конструкцией транспортного средства и физическими условиями проблемы.
Примеры решения проблем по теме «Тяга»
Автомобиль весом 4 тонны движется по ровной дороге с ускорением . Найдите силу тяги двигателя автомобиля, если коэффициент трения .
Мы делаем картину:
При движении по машине сила тяжести , сила реакции опоры , сила трения и тяговое усилие действуют. Под действием этих сил автомобиль движется с ускорением .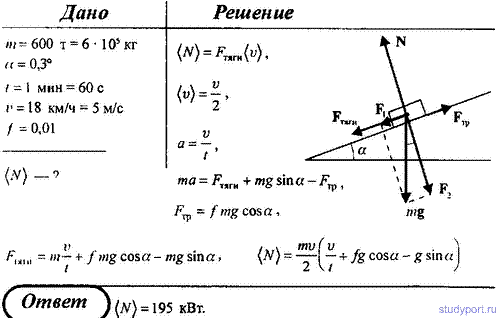
Согласно второму закону Ньютона:
Введем систему координат, как показано на рисунке, и запишем это векторное равенство в проекциях на оси координат.
Сила трения . Из второго уравнения . Поэтому мы можем написать ( . Замените значение силы трения в первом уравнении и определите силу тяги автомобильного двигателя:
Ускорение силы тяжести
Подставляя в формулу численные значения физических величин, вычисляем:
Двигатель двигателя тяги
Автомобиль весом 4 тонны движется в гору с наклоном 1 м на каждые 25 м пути с постоянной скоростью. Найдите силу тяги двигателя автомобиля, если коэффициент трения
Мы делаем картину:
В этом примере, как и в предыдущем, при движении автомобиля сила тяжести , сила реакции поддержки , сила трения и тяговое усилие действуют на автомобиль. И под влиянием этих сил автомобиль движется в гору с постоянной скоростью, то есть ускорение автомобиля .
Согласно второму закону Ньютона:
Запишем это векторное равенство в проекциях на оси координат:
Из второго уравнения и силы трения .
Подставляя значение силы трения в первое уравнение, мы определяем силу тяги:
Сила тяги: определение
Силой тяги называют силу, прикладываемую к телу для поддержании его в постоянном движении.
Прекращение действия силы тяги приводит к остановке вследствие трения, вязкости окружающей среды и других противодействующих движению сил.
Тело, на которое не действуют силы, движется с постоянной скоростью $v = const$ (первый закон Ньютона). Частным случаем такого движения является состояние покоя ($v = 0$). Движение с постоянной скоростью называют состоянием инерции. Чтобы вывести тело из такого состояния, нужно приложить к нему силу. Скорость тела в этом случае изменится, т.е. оно получит ускорение (либо замедление, которое можно считать отрицательным ускорением).
Величина ускорения обратнопропорциональна массе тела (чем оно массивнее, тем труднее его вывести из состояния инерции) и прямопропорциональна интенсивности приложенной силы. Таким образом:
Эта формула отражает Второй закон Ньютона.
Попробуй обратиться за помощью к преподавателям
Формулы для расчета
В качестве примера силы тяги, выводящей тело из состояния покоя, можно рассмотреть спортсмена, поднимающего штангу. В исходном состоянии штанга находится в состоянии инерции (остается неподвижной). Когда спортсмен отрывает ее от земли, его мышцы должны сокращаться с такой силой, чтобы она превысила вес штанги, т.е. силу, с которой ее притягивает гравитационное поле Земли. Если штангисту удастся оторвать штангу от пола – значит она переместится вверх на некоторое расстояние, т.е. получит ускорение. Т.е. силой тяги, двигающей данный снаряд, является сила сокращающихся мышц спортсмена. При этом должно соблюдаться условие:
$F_м$ > $F_т$, т.е. $F_м$ >$ m cdot g$,
где $F_м$ – сила мышц (в данном случае сила тяги), $F_т$ – сила тяжести (гравитация), $m$ – масса, $g$ – ускорение свободного падения.
Состояние движения по инерции следует отличать от равномерного движения, когда сила тяги уравновешивается противодействующими силами. Например, при движении автомобиля работающий двигатель через систему трансмиссии передает на колеса силу, преодолевающую силы трения внутри механизмов автомобиля, трения колес о поверхность дороги, сопротивления воздуха и т.д. Силу тяги можно в этом случае вычислить зная время разгона $t$ до нужной скорости $v$ и массу автомобиля $m$:
Например, при движении автомобиля работающий двигатель через систему трансмиссии передает на колеса силу, преодолевающую силы трения внутри механизмов автомобиля, трения колес о поверхность дороги, сопротивления воздуха и т.д. Силу тяги можно в этом случае вычислить зная время разгона $t$ до нужной скорости $v$ и массу автомобиля $m$:
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Здесь ускорение выражено как частное от деления скорости на время разгона.
Силу тяги можно также выразить через мощность – способность некоторого источника энергии совершать работу. Чем мощность выше – тем за меньшее время этот источник разовьет силу, способную разогнать тело массой $m$ до требуемой скорости $v$. Работа же прямопропорциональна силе, которая ее совершила:
где $s$ – расстояние, на которое сила переместила данное тело.
Поскольку расстояние можно выразить через скорость и время,
а мощность есть работа, выполняемая в единицу времени
можно составить уравнения:
Вычислить силу тяги автомобиля, движущегося с ускорением $3 м/с^2$, если его масса составляет 1,5 тонны, а сила трения – 10% от силы тяжести.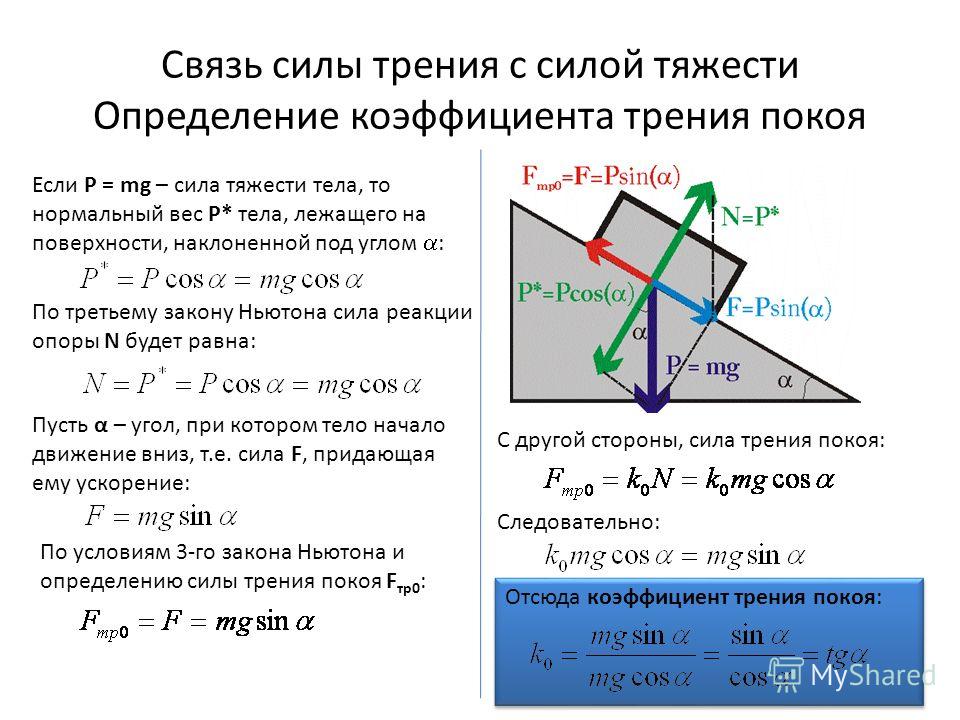
Рассмотрим силу тяги как сумму двух сил:
- разгоняющей автомобиль с заданным ускорением: $F_1 = m cdot a$, где $m$ – масса, $a$ – ускорение;
- преодолевающей силу трения: $F_2 = mu cdot m cdot g$, где $mu$ – коэффициент силы трения, $g$ – ускорение свободного падения.
Подставив числовые значения в формулу
$F = F_1 + F_2 = m cdot a + mu cdot m cdot g$
получим, попутно переведя тонны в единицы СИ килограммы,
$F = 1500 cdot 3 + 0,1 cdot 9,8 cdot 1500 = 1500 cdot (3 + 0,98) = 5970$
Ответ: 5970 ньютонов.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Глава 4. Сила трения
Сила трения возникает при скольжении шероховатых тел по шероховатым поверхностям, или при попытке сдвинуть такие тела вдоль поверхностей. Чтобы сформулировать основные законы, которым подчиняется сила трения, рассмотрим несколько случаев.
Тело аккуратно положили на горизонтальную поверхность, а затем подействовали на него горизонтальной силой , которую в дальнейшем мы будем называть сдвигающей.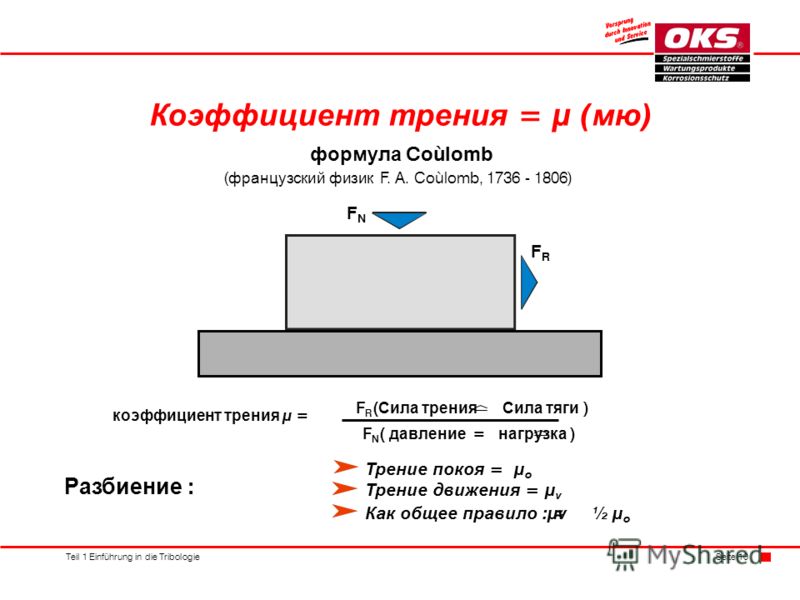 Очевидно, что если сдвигающая сила не достаточна, чтобы сдвинуть тело, то сила трения равна силе (в частности, при нулевой внешней силе сила трения равна нулю — шероховатости тела и опоры «не зацепляются»).
Очевидно, что если сдвигающая сила не достаточна, чтобы сдвинуть тело, то сила трения равна силе (в частности, при нулевой внешней силе сила трения равна нулю — шероховатости тела и опоры «не зацепляются»).
Поскольку тело, свободно лежащее на какой-то поверхности, можно сдвинуть, прикладывая к нему достаточно большую сдвигающую силу, то сила трения между телом и этой поверхностью не может превышать некоторого максимального значения, которое, как это следует из опыта, определяется соотношением
(4.1) |
где — некоторое число, называемое коэффициентом трения, — сила нормальной реакции, действующая между телом и поверхностью. Если тело скользит по поверхности, то, как это также следует из опыта, на тело действует сила трения, равная своему максимальному значению (4.1).
Из этого краткого обзора свойств силы трения следуют правила анализа этой силы.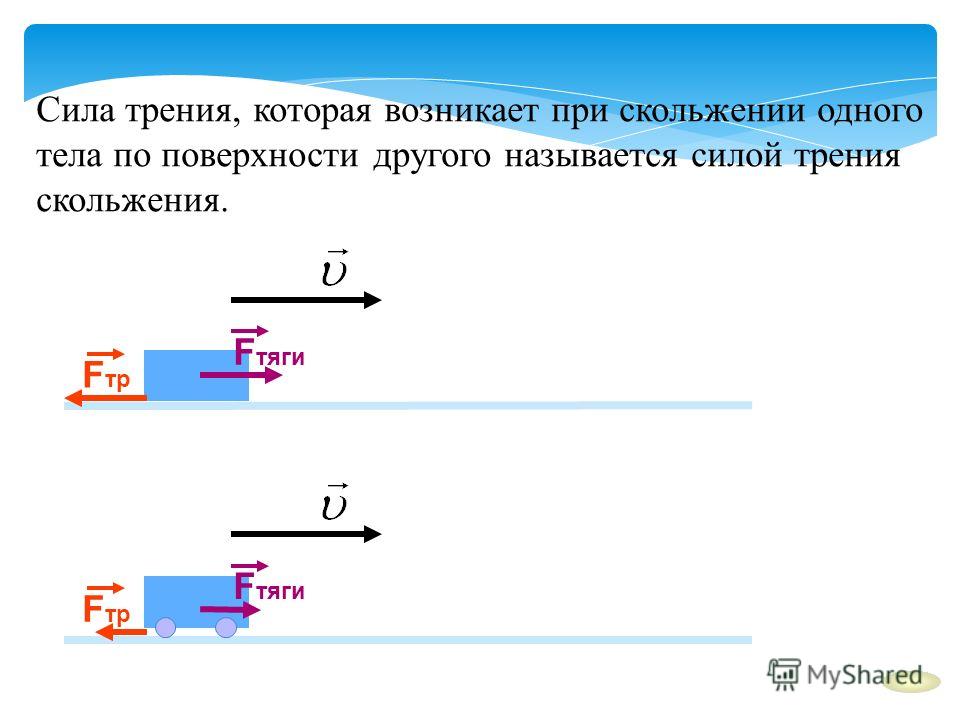 Если в условии задачи говорится, что тело движется по некоторой поверхности, то для силы трения следует использовать закон (4.1) с силой реакции, которую можно найти из проекции второго закона Ньютона на ось, перпендикулярную этой поверхности. Далее с помощью второго закона Ньютона можно исследовать движение тела. Если же задача поставлена так, что тело кладут на поверхность и действуют на него какими-нибудь силами, причем неизвестно, сдвигают эти силы тело, или нет, то требуется дополнительный анализ силы трения. Необходимо сравнить сдвигающую силу (которой является проекция суммарной силы на ось, параллельную поверхности) и максимальную силу трения (4.1). Если сдвигающая сила меньше максимальной силы трения, тело будет покоиться, а сила трения равняться сдвигающей силе. Если сдвигающая сила больше максимальной силы трения (4.1), тело будет двигаться, а действующая на него сила трения будет определяться формулой (4.1). Разберем эти и другие свойства силы трения на примере решения задач.
Если в условии задачи говорится, что тело движется по некоторой поверхности, то для силы трения следует использовать закон (4.1) с силой реакции, которую можно найти из проекции второго закона Ньютона на ось, перпендикулярную этой поверхности. Далее с помощью второго закона Ньютона можно исследовать движение тела. Если же задача поставлена так, что тело кладут на поверхность и действуют на него какими-нибудь силами, причем неизвестно, сдвигают эти силы тело, или нет, то требуется дополнительный анализ силы трения. Необходимо сравнить сдвигающую силу (которой является проекция суммарной силы на ось, параллельную поверхности) и максимальную силу трения (4.1). Если сдвигающая сила меньше максимальной силы трения, тело будет покоиться, а сила трения равняться сдвигающей силе. Если сдвигающая сила больше максимальной силы трения (4.1), тело будет двигаться, а действующая на него сила трения будет определяться формулой (4.1). Разберем эти и другие свойства силы трения на примере решения задач.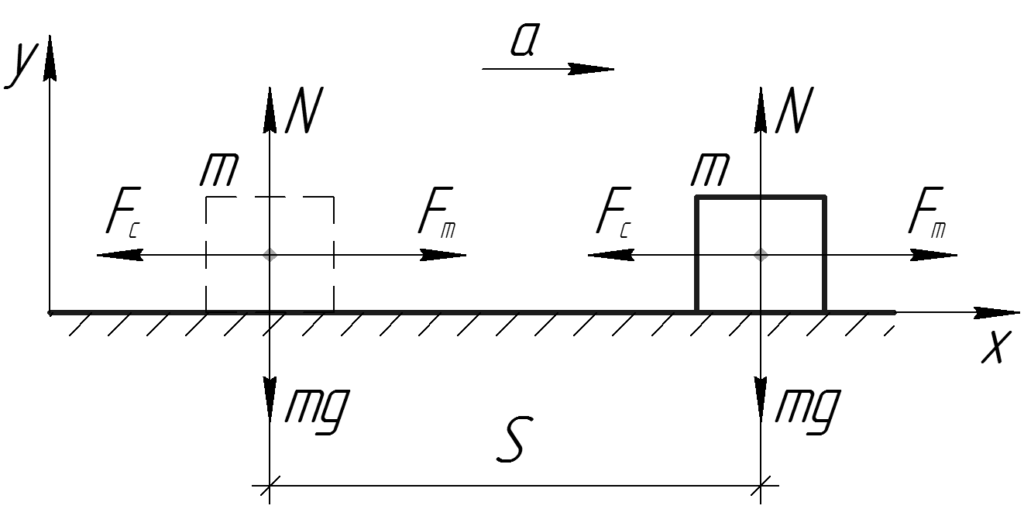
Очевидно, коэффициент трения — безразмерная величина. Действительно, в формуле (4.1) и , и имеют размерность силы, поэтому коэффициент трения — безразмерный (задача 4.1.1 — ответ 4).
В задаче 4.1.2 тело не движется, и никакие силы не стремятся его сдвинуть. Поэтому шероховатости тела и опоры «не зацепляются» и сила трения равна нулю (ответ 2).
В задаче 4.1.3 тело движется по шероховатой горизонтальной поверхности, поэтому сила трения определяется формулой (4.1) и равна (ответ 1).
Из условия задачи 4.1.4 не ясно, будет двигаться данное тело, или нет. Сравнение сдвигающей силы и максимальной силы трения показывает, что данной сдвигающей силы не достаточно, чтобы сдвинуть тело.
Следовательно, тело будет покоиться, а сила трения равняться сдвигающей силе (ответ 2). Из этого анализа следует также, что сдвинуть данное тело может минимальная горизонтальная сила (задача 4. 1.5 — ответ 3).
1.5 — ответ 3).
Аналогичный анализ необходимо выполнить, когда исследуется поведение тела на наклонной плоскости (задача 4.1.6). Если тело аккуратно положить на плоскость, то в зависимости от коэффициента трения и угла наклона плоскости оно может как покоиться, так и скользить. Очевидно, для тела на наклонной плоскости сдвигающей силой является составляющая силы тяжести, параллельная плоскости, т.е.
(см. рисунок). Сила реакции плоскости компенсирует составляющую силы тяжести, перпендикулярную плоскости, и потому равна (параллельная и перпендикулярная плоскости составляющие силы тяжести показаны на рисунке пунктирными стрелками). Поэтому телу будет двигаться, если
(4.2)
или (ответ 2). Или (задача 4.1.7 — ответ 1). Ускорение тела, соскальзывающего с наклонной плоскости, можно найти из второго закона Ньютона (задача 4.1. 8)
8)
Для наклонной плоскости высотой 3 и длиной 5 м , . Отсюда находим, что (ответ 2).
В задачах 4.1.9 и 4.1.10 необходимо выразить коэффициент трения между телом и поверхностью через кинематические характеристики движения тела по этой поверхности. Основная идея решения заключается в том, чтобы из кинематических характеристик найти ускорение тела, а затем из второго закона Ньютона — силу и коэффициент трения. Из законов равноускоренного движения (2.2) и (2.3) находим связь времени движения до остановки и пройденного расстояния
Отсюда получаем . С другой стороны из второго закона Ньютона для тела, движущегося по шероховатой горизон — тальной поверхности, следует, что . Поэтому (задача 4.1.9 — ответ 3).
Аналогично в задаче 4.1.10 из закона равноускоренного движения для скорости ( — начальная скорость, — время движения до остановки) и второго закона Ньютона получаем (ответ 1).
В нескольких следующих задачах также необходимо исследовать возможность движения тела под действием тех или иных сдвигающих сил. В задаче 4.2.1 сдвигающей силой является сила тяжести, а сила реакции и сила трения возникают благодаря прижиманию тела к стенке внешней силой (см. рисунок). Поэтому . Отсюда заключаем, что брусок будет покоиться, пока сила тяжести будет меньше максимальной силы трения . Или (ответ 3).
В задаче 4.2.2 сдвигающей силой является горизонтальная составляющая внешней силы , т.е. . Сила реакции поверхности, как это следует из проекции второго закона Ньютона на вертикальное направление, равна . Поэтому тело начнет двигаться, если . Или
(ответ 1).
Согласно второму закону Ньютона при действии на тело двух взаимно перпендикулярных горизонтальных сил и , сдвигающая сила равна . Поскольку по условию задачи 4.2.3 при и тело движется с пренебрежимо малым ускорением, то . Откуда получаем (ответ 4).
Откуда получаем (ответ 4).
В задаче 4.2.4 цепочка начинает соскальзывать со стола, когда сила тяжести, действующая на свисающий со стола конец цепочки ( ) , сравнивается с максимальной силой трения, действующей на ее часть, лежащую на столе ( ) . Поэтому (ответ 2).
График зависимости силы трения от сдвигающей силы (задача 4.2.5) строится следующим образом. При малых значениях сдвигающей силы тело покоится, а сила трения равна сдвигающей силе. Когда же сдвигающая сила превосходит максимальную силу трения , то сила трения не зависит от сдвигающей силы:
График, правильно представляющий эту зависимость, дан на рисунке 4.
Аналогичные рассуждения позволяют построить график зависимости ускорения тела от сдвигающей силы (задача 4.2.6). Для значений сдвигающей силы, не превосходящих максимальную силу трения, тело покоится и его ускорение равно нулю. Если сдвигающая сила превосходит максимальную силу трения , ускорение тела находится из второго закона Ньютона: . Правильный график приведен на рисунке 1.
Правильный график приведен на рисунке 1.
На тело со стороны наклонной плоскости в задаче 4.2.7 действуют перпендикулярная плоскости сила реакции и сила трения, направленная вверх вдоль плоскости, причем поскольку тело движется, сила трения достигает своего максимального значения. Чтобы найти направление вектора суммы этих сил заметим, что поскольку первоначально тело покоилось на плоскости, то в этом положении сумма силы нормальной реакции и силы трения, которая меньше максимальной, направлена вертикально вверх. Поэтому правильный ответ для направления суммы сил трения и реакции в случае движения тела вниз по плоскости дает рисунок 2.
Движение тела в задаче 4.2.8 в системе отсчета, связанной с лентой, происходит следующим образом. На покоящуюся ленту попадает тело, имеющее скорость , замедляется под действием силы трения, а затем останавливается. При этом пока тело перемещается относительно ленты, на него действует постоянная сила трения . Поэтому ускорение тела постоянно и равно . Применяя закон равноускоренного движения для скорости (2.3) к моменту остановки тела относительно ленты
Поэтому ускорение тела постоянно и равно . Применяя закон равноускоренного движения для скорости (2.3) к моменту остановки тела относительно ленты
где — время, прошедшее от начала движения тела по ленте до его остановки, получаем (ответ 2).
Очевидно, правильным графиком зависимости скорости от времени в задаче 4.2.9 является график 1. Действительно, после остановки в верхней точке тело начнет соскальзывать по плоскости вниз, так как (задача 4.1.6). Следовательно, график 3. не подходит. При движении тела вниз проекция его скорости на ось отрицательна, поэтому не подходит и график 4. А поскольку ускорение тела при его движении вверх больше ускорения при движении вниз , наклон второй части графика зависимости скорости от времени должен быть меньше его наклона при движении вниз.
При движении тела по доске в задаче 4.2.10 на доску в горизонтальном направлении действуют силы трения со стороны тела и со стороны поверхности , направленные так, как показано на рисунке. Это значит, что сила трения, действующая на доску со стороны тела, стремится заставить ее двигаться, со стороны поверхности — не дать доске двигаться. Поэтому поведение доски определяется сравнением этих сил. А поскольку сила трения между доской и телом равна ( — масса тела, сила трения выражена в Ньютонах), максимальная сила трения между доской и поверхностью — ( — масса доски, сила трения также выражена в Ньютонах), то доска будет двигаться (ответ 1).
Это значит, что сила трения, действующая на доску со стороны тела, стремится заставить ее двигаться, со стороны поверхности — не дать доске двигаться. Поэтому поведение доски определяется сравнением этих сил. А поскольку сила трения между доской и телом равна ( — масса тела, сила трения выражена в Ньютонах), максимальная сила трения между доской и поверхностью — ( — масса доски, сила трения также выражена в Ньютонах), то доска будет двигаться (ответ 1).
Как найти силу тяги зная
Что такое сила тяги и по какой формуле её находить ?
Разберёмся в вопросе, что такое сила тяги. Как следует из самого названия – это сила, которую необходимо прикладывать к телу, чтобы оно находилось в состоянии постоянного движения.
Если её убрать, то тело, будь то автомобиль, электровоз, космическая ракета или санки, со временем остановится. Это произойдёт потому, что на тело всегда действуют силы, которые заставляют его стремиться к состоянию покоя:
- силы трения (покоя, качения, скольжения),
- сопротивления воздуха (газа),
- сопротивления воды и др.

Первый и второй законы Ньютона
Обратимся к законам Ньютона, которые хорошо описывают механическое движение тел. Из школьной программы мы знаем, что есть первый закон Ньютона, который описывает закон инерции. Он гласит, что любое тело, если на него не действуют силы, или если их равнодействующая равна нулю, движется прямолинейно и равномерно, или же находится в состоянии покоя. Это означает, что тело, пока на него ничто не действует, будет двигаться с постоянной скоростью v=const или пребывать в состоянии покоя сколько угодно долго, пока какое-то внешнее воздействие не выведет тело из этого состояния. Это и есть движение по инерции.
Надо сказать, что этот закон справедлив лишь в так называемых инерциальных системах отсчёта. В неинерциальных системах отсчёта этот закон не действует и нужно использовать второй закон Ньютона. В таких системах отсчёта тело тоже будет двигаться по инерции, но оно будет двигаться с ускорением, стремясь сохранять своё движение, т. е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.
е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.
Этот закон утверждает, что для того, чтобы вывести тело из состояния покоя или равномерного движения, к нему необходимо приложить силу, равную F=m•a, где m — это масса тела, a — ускорение, сообщаемое телу. Зная эти законы, можно рассчитать силу тяги (двигателя автомобиля, ракетного двигателя или, например, лошади, тянущей нагруженную повозку).
Примеры из жизни
Насколько вы сильны?
Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.
Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.
Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.
Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.
Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).
Насколько силён ваш автомобиль?
Рассмотрим ещё пример. У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
Допустим, вы разогнали свой автомобиль до скорости v за какое-то время t, проехав расстояние s. Тогда Fтяги будет легко рассчитана по формуле: Fтяги = m•v/t. Как и в примере с санками, справедлива также такая формула: Fтяги = f•m•g, где f – коэффициент трения качения, который зависит от скорости автомобиля (чем больше скорость, тем меньше этот коэффициент).
Но что делать, если масса автомобиля m, коэффициент трения качения f и время разгона t неизвестны ? Тогда можно поступить по-другому. Двигатель вашего автомобиля при разгоне совершил работу A = Fтяги • s. Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Допустим, вы разогнали свой автомобиль до скорости v = 180 км/ч, а мощность его двигателя N = 200 л. с. (лошадиных сил). Чтобы вычислить Fтяги двигателя, необходимо прежде перевести указанные единицы измерения в единицы СИ, т. е. международной системы измерения. Здесь 1 л. с. = 735,499 Вт, поэтому мощность двигателя составит N = 200 л. с. • 735,499 Вт/л. с. = 147099,8 Вт. Скорость в системе СИ будет равна v = 180 км/ч = 180 • 1000 м/3600 с = 50 м/с. Тогда искомое значение будет равно Fтяги = 147099,8 Вт/50 (м/с) = 2941,996 Н
2,94 кН (килоньютона).
Около 3 килоньютонов. Много это или мало ? Допустим, вы жмёте 100 килограммовую штангу. Чтобы её поднять, вам нужно преодолеть её вес, равный P = m•g = 100 кг • 9,81 м/с² = 981 Н (ньютон)
0,98 кН. Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Таким образом, зная школьный курс физики, мы можем с лёгкостью вычислить силу тяги:
- человека,
- лошади,
- паровоза,
- автомобиля,
- космической ракеты и всех прочих видов техники.
В нашем видео вы найдете интересные опыты, поясняющие, что такое сила тяги и сила сопростивления.
Формула силы тяги
Само по себе понятие «сила тяги» имеет смысл только применительно к какому-нибудь транспортному средству, к примеру, говорят о силе тяги автомобиля, самолета, лошади, тянущей сани.
Единица измерения силы – Н (ньютон).
Очень заманчиво заключить, что источником силы тяги автомобиля является его двигатель. Однако, это неверно. Внутренние силы одной части системы (двигателя), воздействуя на другую часть системы (колеса), не могут придать ускорение всей системе в целом (всему автомобилю), так как это противоречит закону сохранения импульса. Источником силы тяги являются внешние воздействия. В случае автомобиля – это сила трения колес о дорожное покрытие, в случае корабля – сила водной струи, отбрасываемой винтом.
В случае автомобиля – это сила трения колес о дорожное покрытие, в случае корабля – сила водной струи, отбрасываемой винтом.
Одной универсальной формулы для расчета силы тяги нет. Сила тяги определяется конструкцией транспортного средства и физическими условиями задачи.
Примеры решения задач по теме «Сила тяги»
| Задание | Автомобиль массой 4 т движется по ровной дороге с ускорением 4 м/с . Найти силу тяги двигателя автомобиля, если коэффициент трения . |
| Решение | Сделаем рисунок: |
При движении на автомобиль действуют сила тяжести , сила реакции опоры , сила трения и сила тяги . Под действием этих сил автомобиль движется с ускорением .
По второму закону Ньютона:
Введем систему координат, как показано на рисунке, и запишем это векторное равенство в проекциях на координатные оси.
Сила трения . Из второго уравнения . Поэтому можно записать . Подставим значение силы трения в первое уравнение и определим силу тяги автомобильного двигателя:
Ускорение свободного падения м/с
Подставив в формулу численные значения физических величин, вычислим:
| Задание | Автомобиль массой 4 т движется в гору с уклоном 1 м на каждые 25 м пути с постоянной скоростью. 2. Если силу трения считать равной 0,06 Н, то горизонтально направленная сила тяги, прикладываемая к телу, равна: 2. Если силу трения считать равной 0,06 Н, то горизонтально направленная сила тяги, прикладываемая к телу, равна: 1) 0,02 Н 2) 0,08 Н 3) 0,2 Н 4) 0,8 Н Возможно так: Формулы такой нет. Это выдержка из объяснения. Пусть m – секундный расход топлива, u – скорость истечения газов из сопла двигателя относительно ракеты (относительно ракеты) , m > 0 и u > 0, (D — приращение, то есть «дельта».) Работающий двигатель как бы “забирает” у ракеты непрерывно, порция за порцией, горючее и, сжигая его в камере сгорания, выбрасывает, образуя реактивную струю. Пусть в некоторый момент времени двигатель “забрал” порцию горючего массой D m. За малый промежуток времени D t масса D m сгорает и выбрасывается из сопла двигателя с относительной скоростью u в направлении, противоположном движению ракеты, то есть скоростью v – u относительно Земли. Вначале, при v < u, абсолютная скорость истечения газов отрицательна (направлена к Земле) , а позже, когда v > u, положительна (направлена от Земли) . После сгорания выбрасываемая масса обладает абсолютным количеством движения следовательно, за время приращения её количества движения составит: ( v – u) D m – v D m = –u D m. В единицу времени изменение количества движения массы равно – u D m / D t. Физически эта величина представляет собой силу F ‘ давления на струю, создаваемую работой реактивного двигателя. Учитывая, что D m / D t = m, получаем: Знак “минус” показывает, что сила F ‘, действующая на образующуюся газовую струю, направлена к Земле. По третьему закону Ньютона при взаимодействии двигателя с выбрасываемой им струёй последняя действует на двигатель ракеты в противоположную сторону с силой F = – F ‘, то есть Её называют реактивной силой. Таким образом, при стационарном режиме работы реактивного двигателя сила тяги постоянна, направлена вверх (в сторону движения корабля) и равна произведению секундного расхода топлива на относительную скорость выбрасываемых газов. Зная реактивную силу, можно написать уравнение движения ракеты, которое без учёта поля тяготения имеет вид: m D v / D t = m u, (3) где D v / D t – ускорение ракеты. При наличии поля тяготения уравнение движения будет: m D v / D t = m u – m g. (4) Внешнее силовое поле не изменяет величины создаваемой двигателем реактивной силы, так как последняя определяется лишь режимом работы самого двигателя ракеты, оно меняет только закон движения корабля. Интегрируя уравнение (3), К. Э. Циолковский впервые нашёл, что скорость корабля в пространстве вне поля тяготения возрастает по логарифмическому закону: Калькулятор удельного импульса Этот калькулятор удельного импульса поможет вам оценить характеристики реактивного или ракетного двигателя . Двигатель с более высокое значение удельного импульса является более эффективным , поскольку он производит большую тягу на массу топлива или топлива. Это также зависит от функции и типа двигателя; например, удельный импульс ракетного двигателя намного ниже, чем у реактивного двигателя. Уравнение удельного импульса помогает в начальном анализе приблизительно оценить размер двигателя и требуемый массовый расход топлива. Итак, что такое удельный импульс? Читайте дальше, чтобы понять конкретную формулу импульса и ее использование. Что такое удельный импульс? Удельный импульс — это время, в течение которого двигатель может создать силу тяги, равную его массе при I=∫F dt\quad I = \int F \,dtI=∫Fdt Удельные импульсы измеряем в единицах времени, т. е. в секундах. Это делает этот параметр удобным способом сравнения производительности разных двигателей. Удельный импульс показывает, насколько эффективно расходуется топливо. Более высокое значение удельного импульса означает, что ракета будет эффективно подниматься на большую высоту. Формула удельного импульсаУравнение удельного импульса для двигателя, создающего тягу, FFF, с массовым расходом m˙\dot mm˙: Isp=Fm˙g0\quad I_{sp} = \frac{F}{\dot{m}g_0}Isp=m˙g0F Если вы не знаете тягу, создаваемую двигателем имея сухую массу, WWW, можно использовать тяговооруженность TrT_rTr , для ее оценки, которая равна: }{W} \ подразумевает I_{sp} = \frac{WT_r}{\dot{m}g_0}Tr=WF⟹Isp=m˙g0WTr Однако тяга FFF также связана к скорости истечения vev_eve как: F=m˙ve ⟹ Isp=veg0\quad F = \dot{m} v_e \implies I_{sp} = \frac{v_e}{g_0} F=m˙ve⟹Isp=g0ve Удельный расход топлива по тяге (TSFC): Топливная эффективность двигателя. TSFC=m˙F\quad\text{TSFC} = \frac{\dot m}{F}TSFC=Fm˙ Обратный параметр Fs=Fm˙\quad F_s = \frac{F}{\dot m}Fs=m˙F Как рассчитать удельный импульс Калькулятор имеет технические данные для некоторых двигателей, которые вы можете использовать напрямую. Если вашей конфигурации нет в списке, используйте Для расчета удельного импульса:
💡 Вы можете использовать расширенный режим Пример: С помощью калькулятора удельного импульса Определите удельный импульс двигателя, развивающего тягу
Isp=veg0=200009. Часто задаваемые вопросыЧто вы подразумеваете под удельным импульсом?Удельный импульс — это параметр, который сообщает нам для , сколько секунд двигатель будет развивать один фунт тяги, используя один фунт топлива или топлива . Другими словами, удельный импульс является мерой того, как долго двигатель может непрерывно создавать тягу, полностью сжигая единицу массы топлива . Непрерывная тяга подразумевает ускорение тела, прикрепленного к двигателю. Как рассчитать удельный импульс?Для расчета удельного импульса двигателя:
В качестве альтернативы:
Какова единица измерения удельного импульса? Единицей измерения удельного импульса является Что такое удельный расход топлива по тяге? Расход топлива в массе в секунду для создания единичной выходной тяги. Этот параметр также считается топливной экономичностью двигателя. Математически это отношение массового расхода и тяги, произведенной , и выражается в единицах Основы космического полета: ракетное движение
Исаак Ньютон заявил в своем третьем законе движения, что «на каждое действие есть равное и противоположное противодействие». Именно по этому принципу работает ракета. Пропелленты объединяются в камере сгорания, где они химически реагируют с образованием горячих газов, которые затем ускоряются и выбрасываются с высокой скоростью через сопло, тем самым придавая импульс двигателю.  Сила тяги ракетного двигателя — это реакция конструкции двигателя на выброс высокоскоростного вещества. Это то же самое явление, которое толкает садовый шланг назад, когда вода вытекает из сопла, или вызывает отдачу ружья при выстреле. Сила тяги ракетного двигателя — это реакция конструкции двигателя на выброс высокоскоростного вещества. Это то же самое явление, которое толкает садовый шланг назад, когда вода вытекает из сопла, или вызывает отдачу ружья при выстреле.Тяга Тяга — это сила, которая приводит в движение ракету или космический корабль и измеряется в фунтах, килограммах или ньютонах. Физически говоря, это результат давления, оказываемого на стенку камеры сгорания. На рис. 1.1 показана камера сгорания с отверстием, соплом, через которое может выходить газ. Распределение давления внутри камеры несимметрично; т. е. внутри камеры давление меняется мало, а вблизи сопла несколько уменьшается. Сила от давления газа на дно камеры не компенсируется извне. Результирующая сила F из-за разницы внутреннего и внешнего давления, тяга, противоположна направлению газовой струи. Он толкает камеру вверх. Для создания высокоскоростных выхлопных газов необходимые высокие температуры и давления сгорания достигаются за счет использования очень энергичного топлива и максимально низкой молекулярной массы выхлопных газов. Тяга F является равнодействующей сил, обусловленных давлением, оказываемым на внутреннюю и внешнюю стенки дымовыми газами и окружающей атмосферой, принимая границу между внутренней и внешней поверхностями за поперечное сечение выхода сопло. Как мы увидим в следующем разделе, применение принципа сохранения импульса дает , где q — массовый расход выбрасываемого газа, P a — давление окружающей атмосферы, P e — давление выхлопных газов и V e — скорость их выброса. Тяга указывается либо на уровне моря, либо в вакууме. Сохранение импульса Линейный импульс ( p ), или просто импульс , частицы есть произведение ее массы на скорость. Ньютон выразил свой второй закон движения в терминах импульса, который можно сформулировать так: «равнодействующая сил, действующих на частицу, равна скорости изменения линейного импульса частицы». В символической форме это становится , что эквивалентно выражению F=ma . Если у нас есть система частиц, общий импульс P системы есть сумма импульсов отдельных частиц. Когда результирующая внешняя сила, действующая на систему, равна нулю, полный линейный импульс системы остается постоянным. Это называется принципом сохранения импульса . Давайте теперь посмотрим, как этот принцип применяется к ракетной механике. Рассмотрим ракету, дрейфующую в свободном от гравитации пространстве. Двигатель ракеты работает в течение времени t и в течение этого времени выбрасывает газы с постоянным расходом и с постоянной скоростью относительно ракеты (скорость истечения). Предположим, что внешние силы, такие как гравитация или сопротивление воздуха, отсутствуют. Рисунок 1.2(a) показывает ситуацию в момент времени t . Ракета и топливо имеют общую массу 90 245 M 90 246, и эта комбинация движется со скоростью 90 245 v 90 246, если смотреть из конкретной системы отсчета. В момент времени 90 245 t 90 246 позже конфигурация изменилась на показанную на рисунке 1.2 (b). Масса M была выброшена из ракеты и движется со скоростью u , видимой наблюдателем. Ракета уменьшена до массы М- М и скорости v ракеты заменен на v+v . Поскольку внешние силы отсутствуют, dP/dt=0 . Мы можем написать для интервала времени t , где P 2 — конечный импульс системы, рис. 1.2(b), а P 1 — начальный импульс системы, рис. 1.2(a). Мы пишем Если мы позволим t приблизиться к нулю, v/t приблизится к dv/dt , ускорению тела. Количество M есть масса, выброшенная в t ; это приводит к уменьшению массы M исходного кузова. Правый член зависит от характеристик ракеты и, как и левый член, имеет размерность силы. Эта сила называется тягой и представляет собой силу реакции, действующую на ракету со стороны покидающей ее массы. Конструктор ракеты может сделать тягу максимально возможной, спроектировав ракету так, чтобы выбрасывать массу как можно быстрее (9).0245 dM/dt большой) и с максимально возможной относительной скоростью ( V отн большой). В ракетной технике основное уравнение тяги записывается как где q — массовый расход выбрасываемого газа, V e — скорость выброса выхлопных газов, P e — давление выхлопных газов на выходе из сопла, P a — давление окружающей атмосферы, а A e — площадь выходного отверстия сопла. (для возврата используйте функцию «назад» вашего браузера) Уравнение (1.6) может быть упрощено определением эффективной скорости отработавших газов, С, определяемой как Уравнение (1.6) затем сводится к Импульс и импульс В предыдущем разделе мы видели, что второй закон Ньютона может быть выражен в форме Умножая обе части на dt и интегрируя от времени t 1 до времени t 2 , мы пишем Интеграл представляет собой вектор, известный как линейный импульс или просто импульс силы F в течение рассматриваемого интервала времени. Когда на частицу действует несколько сил, необходимо учитывать импульс каждой из сил. Когда проблема связана с системой частиц, мы можем векторно сложить импульсы всех частиц и импульсы всех задействованных сил. Когда можно тогда написать Для интервала времени t можно записать уравнение (1.10) в виде Давайте теперь посмотрим, как мы можем применить принцип импульса и количества движения к ракетной механике. Рассмотрим ракету с начальной массой M , которую она запустила вертикально в момент времени t =0. Топливо расходуется с постоянной скоростью q и выбрасывается с постоянной скоростью V e относительно ракеты. Пишем Делим на t и заменяем u-(v+v) на V e , скорость выбрасываемой массы относительно ракеты. При стремлении t к нулю получаем Разделяя переменные и интегрируя от t =0, v =0 до t=t, v=v , получаем что равно Член -gt в уравнении (1.15) является результатом гравитации Земли, притягивающей ракету. Для ракеты, дрейфующей в космосе, -gt неприменим и может быть опущен. Обратите внимание, что M представляет начальную массу ракеты и M-qt конечная масса. Поэтому уравнение (1.16) часто записывают как , где m o /m f называется отношением масс . Уравнение (1.17) также известно как ракетное уравнение Циолковского, названное в честь русского пионера ракетостроения Константина Э. Циолковского (1857-1935), который первым вывел его. На практике переменная V e обычно заменяется эффективной скоростью выхлопных газов, С . Таким образом, уравнение (1.17) принимает вид В качестве альтернативы мы можем написать , где e — математическая константа, приблизительно равная 2,71828. Для многих маневров космического корабля необходимо рассчитать продолжительность работы двигателя, необходимую для достижения определенного изменения скорости. Переставляя переменные, мы имеем Скорость сгорания и выхлопа Процесс сгорания включает окисление компонентов топлива, которые способны к окислению, и поэтому может быть представлен химическим уравнением. В процессе горения масса каждого элемента остается неизменной. Рассмотрим реакцию метана с кислородом. Это уравнение утверждает, что один моль метана реагирует с двумя молями кислорода с образованием одного моля углекислого газа и двух молей воды. Это также означает, что 16 г метана реагируют с 64 г кислорода с образованием 44 г углекислого газа и 36 г воды. Все исходные вещества, подвергающиеся процессу горения, называются реагенты , а вещества, образующиеся в результате процесса горения, называются продуктами . Вышеупомянутая реакция горения является примером стехиометрической смеси , то есть кислорода достаточно для химической реакции со всем топливом. В этих условиях достигается самая высокая температура пламени, однако часто желательно эксплуатировать ракетный двигатель при «богатом топливом» соотношении смеси. Соотношение смеси определяется как массовый расход окислителя, деленный на массовый расход топлива. Рассмотрим следующую реакцию керосина (1) с кислородом: Учитывая, что молекулярная масса C 12 H 26 равна 170, а O 2 равна 32, мы имеем отношение смеси , что характерно для многих ракетных двигателей, работающих на керосине или топливе РП-1. Оптимальное соотношение компонентов смеси, как правило, обеспечивает максимальную производительность двигателя (измеряется удельный импульс ), однако в некоторых ситуациях другое отношение O/F приводит к улучшению общей системы. Как мы видели ранее, импульсная тяга равна произведению массового расхода топлива на скорость выброса выхлопных газов. Идеальная скорость выхлопа определяется выражением , где k — коэффициент удельной теплоемкости, R* — универсальная газовая постоянная (8 314,4621 Дж/кмоль-K в единицах СИ или 49 720 фут-фунт/(слаг-моль) — o R в единицах США ), T c – температура горения, M — средний молекулярный вес выхлопных газов, P c — давление в камере сгорания, P e — давление на выходе из сопла. Коэффициент теплоемкости (2) варьируется в зависимости от состава и температуры выхлопных газов, но обычно составляет около 1,2. Термодинамика, связанная с расчетом температуры горения, довольно сложна, однако температура пламени обычно колеблется от 2500 до 3600°С.0640 o C (4500-6500 o F). Давление в камере может находиться в диапазоне примерно от 7 до 250 атмосфер. P e должно быть равно атмосферному давлению, при котором будет работать двигатель, подробнее об этом позже. Из уравнения (1.22) мы видим, что высокая температура и давление в камере сгорания, а также низкий молекулярный вес выхлопных газов приводят к высокой скорости выброса и, следовательно, к высокой тяге. Исходя из этого критерия, мы можем понять, почему жидкий водород очень желателен в качестве ракетного топлива. Следует отметить, что в процессе горения будет происходить диссоциация молекул между продуктами. Если вы хотите узнать больше о термодинамике ракетных двигателей, прочитайте приложение «Ракетная термодинамика». Или вы можете пропустить всю науку и просто найти нужные вам числа. См. Таблицы горения пороха, чтобы найти оптимальное соотношение смеси, температуру адиабатического пламени, молекулярную массу газа и удельную теплоемкость для некоторых распространенных ракетных топлив.
Удельный импульс Удельный импульс ракеты, I sp , есть отношение тяги к расходу выбрасываемого груза, т.е. где F тяга, q — скорость массового расхода, а г o — стандартная сила тяжести (9,80665 м/с 2 ). Удельный импульс выражается в секундах. Когда тяга и расход остаются постоянными в течение всего времени горения топлива, удельным импульсом является время, в течение которого ракетный двигатель обеспечивает тягу, равную весу израсходованного топлива. Для данного двигателя удельный импульс имеет разные значения на земле и в космическом вакууме, поскольку в выражении для тяги участвует давление окружающей среды. Поэтому важно указать, является ли значение удельного импульса значением на уровне моря или в вакууме. В ракетном двигателе имеется ряд потерь, основные из которых связаны с неэффективностью процесса химической реакции (горения), потерями на сопле и потерями на насосах. В целом потери влияют на эффективность удельного импульса. Это отношение реального удельного импульса (на уровне моря или в вакууме) к теоретическому удельному импульсу, полученному с идеальным соплом от газов, поступающих в результате полной химической реакции. Расчетные значения удельного импульса на несколько процентов превышают достигнутые на практике. Из уравнения (1.8) мы можем заменить F на F в уравнении (1.23) qC , получив таким образом Уравнение (1. Другим важным показателем качества для оценки характеристик ракеты является характеристическая скорость истечения , C* (произносится как «звезда C»), которая является мерой энергии, доступной в процессе сгорания, и определяется выражением , где P c — давление в камере сгорания, а A t — площадь горловины сопла. Доставляемые значения C* находятся в диапазоне от примерно 1333 м/с для монотопливного гидразина до примерно 2360 м/с для криогенного кислорода/водорода. Ракетные двигатели Типичный ракетный двигатель состоит из сопла, камеры сгорания и форсунки, как показано на рис. 1.4. В камере сгорания происходит сгорание топлива под высоким давлением. Форсунка Форсунка предназначена для преобразования химико-тепловой энергии, вырабатываемой в камере сгорания, в кинетическую энергию. Сопло преобразует медленно движущийся газ с высоким давлением и высокой температурой в камере сгорания в высокоскоростной газ с более низким давлением и температурой. Поскольку тяга является произведением массы и скорости, желательна очень высокая скорость газа. Сопла состоят из сужающейся и расширяющейся частей. Минимальная площадь проходного сечения между сужающейся и расширяющейся частями называется критической частью сопла. Площадь потока в конце расширяющейся части называется выходным сечением сопла. Таким образом, мы видим, что насадка рассчитана на высоту, на которой она должна работать. У поверхности Земли при атмосферном давлении на уровне моря (0,1 МПа или 14,7 фунта на кв. дюйм) выброс выхлопных газов ограничивается отрывом струи от стенки сопла. В космическом вакууме этого физического ограничения не существует. Следовательно, должно быть два разных типа двигателей и сопел: те, которые продвигают первую ступень ракеты-носителя через атмосферу, и те, которые приводят в движение последующие ступени или контролируют ориентацию космического корабля в космическом вакууме. Площадь горловины сопла, A t , можно найти, если известен общий расход топлива и выбраны топливо и условия работы. Предполагая теорию идеального газа, мы имеем где q — массовый расход топлива, P t — давление газа на срезе сопла, T t — температура газа на срезе сопла, R* — универсальный газ постоянная и k – коэффициент удельной теплоемкости. P t и T t даны , где P c — давление в камере сгорания, а T c — температура пламени в камере сгорания. Горячие газы должны расширяться в расширяющейся части сопла для получения максимальной тяги. Давление этих газов будет уменьшаться, поскольку энергия используется для ускорения газа. Надо найти тот участок сопла, где давление газа равно внешнему атмосферному давлению. Число Маха Н м — отношение скорости газа к локальной скорости звука. Число Маха на выходе из сопла определяется выражением расширения идеального газа , где P a — давление окружающей атмосферы. Площадь выходного отверстия сопла, A e , соответствующая выходному числу Маха, определяется как Коэффициент сечения или коэффициент расширения определяется как площадь выхода A e , деленная на площадь горловины A t . Для ракет-носителей (особенно первых ступеней), где давление окружающей среды меняется в течение периода горения, выполняются расчеты траектории для определения оптимального выходного давления. Однако дополнительным ограничением является максимально допустимый диаметр выходного конуса сопла, который в некоторых случаях является ограничивающим ограничением. (Для получения дополнительной информации см. Дополнение № 1: Оптимизация расширения для достижения максимальной тяги.) Поскольку скорость потока газов в сужающемся сечении сопла ракеты относительно мала, любое гладкое и округлое сужающееся сопло будет иметь очень низкие потери энергии. Напротив, контур расширяющейся секции сопла очень важен для производительности из-за очень высоких скоростей потока. На выбор оптимальной формы сопла для данной степени расширения обычно влияют следующие конструктивные соображения и цели: (1) равномерный, параллельный, осевой поток газа на выходе из сопла для максимального вектора импульса, (2) минимальные потери на отрыв и турбулентность внутри сопла, (3) максимально короткая длина сопла для минимальной оболочки пространства, веса, потерь на трение стенок и требований к охлаждению, и (4) простота изготовления. Коническое сопло: В первых ракетных двигателях почти исключительно использовалось коническое сопло, которое во многих отношениях оказалось удовлетворительным. Коническое сопло обеспечивает простоту изготовления и гибкость при преобразовании существующей конструкции в более высокую или более низкую степень расширения без серьезной модификации конструкции. Конфигурация типичного конического сопла показана на рис. 1.4. Горловина сопла имеет контур дуги окружности радиусом R , в диапазоне от 0,25 до 0,75 диаметра горловины, D t . Полуугол сечения сужающегося конуса сопла может составлять от 20 до 45 градусов. Полуугол расходящегося конуса изменяется примерно от 12 до 18 градусов. Коническое сопло с полууголком раскрытия 15 градусов стало почти стандартом, потому что это хороший компромисс с точки зрения веса, длины и производительности. Поскольку в коническом сопле возникают определенные потери производительности из-за неосевой составляющей скорости выхлопных газов, при расчете импульса выхлопных газов применяется поправочный коэффициент . Сопло в виде колокола: Для повышения производительности и уменьшения длины инженеры разработали сопло в форме колокола. В нем используется участок быстрого расширения (радиальный поток) в начальной расширяющейся области, что приводит к однородному аксиально направленному потоку на выходе из сопла. Контур стены изменяется достаточно постепенно, чтобы предотвратить косые толчки. Эквивалентное полуугловое коническое сопло с углом наклона 15 градусов обычно используется в качестве стандарта для определения раструбных сопел. Например, длина раструбного сопла 80% (расстояние между горловиной и выходной плоскостью) составляет 80% длины конического сопла с половинным углом наклона 15 градусов, имеющего такую же площадь горловины, радиус ниже горловины и коэффициент расширения площади. Одним из удобных способов расчета контура раструбного сопла, близкого к оптимальному, является использование процедур параболической аппроксимации, предложенных Г.В.Р. Рао. Конструктивная конфигурация параболического аппроксимирующего колоколообразного сопла показана на рис. 1.5. Контур сопла непосредственно перед горловиной T представляет собой дугу окружности с радиусом 1,5 R t . Контур сопла расширяющейся секции состоит из круглого входного сечения радиусом 0,382 R t от горловины T до точки N и оттуда по параболе до выхода E . Для проектирования конкретного сопла необходимы следующие данные: диаметр горловины D t , осевая длина сопла от горловины до выходной плоскости L n (или желаемая дробная длина, L f , исходя из 15-градусного конического сопла), степень расширения , начальный угол стенки параболы n и угол выходной стенки сопла e . Камера сгорания Камера сгорания служит оболочкой для удержания компонентов топлива в течение достаточного периода времени, чтобы обеспечить полное смешивание и сгорание. Требуемое время пребывания или время пребывания при горении зависит от многих параметров. Теоретически требуемый объем камеры сгорания зависит от массового расхода топлива, средней плотности продуктов сгорания и времени пребывания, необходимого для эффективного сгорания. Это отношение может быть выражено следующим уравнением: , где V c — объем камеры, q — массовый расход топлива, V — средний удельный объем, t с — время пребывания топлива. Полезным параметром, связанным с объемом камеры и временем пребывания, является характеристическая длина , L* (произносится как «звезда L»), объем камеры, деленный на площадь звукового сечения сопла: Концепцию L* гораздо легче визуализировать, чем более неуловимое «время горения», выраженное в малых долях секунды. Поскольку значение A t почти прямо пропорционально произведению q и V , L* по существу является функцией t s . Обычный метод определения L* новой конструкции камеры тяги в значительной степени опирается на прошлый опыт работы с аналогичным топливом и размером двигателя. При заданном наборе рабочих условий, таких как тип топлива, соотношение смеси, давление в камере, конструкция форсунки и геометрия камеры, минимальное требуемое значение L* можно оценить только по фактическому срабатыванию экспериментальных пусковых камер.
гидродинамика — реактивная тяга бутылки с водой — два метода расчета не соответствуют спросил Изменено 2 года, 11 месяцев назад Просмотрено 6к раз $\begingroup$ Я запускаю ракеты из бутылок с водой со своими детьми, и мы сейчас создаем симуляцию запуска с использованием численных методов. Можете ли вы дать мне интуитивное объяснение, почему два приведенных ниже метода дают разницу в 2,0 для тяги? Какой метод правильный? 92=2P/\rho$ Суммируя, мы видим, что тяга равна удвоенной площади сопла, умноженной на давление. $F=2AP$ Второй методНа изображении ниже кажется, что тяга ракеты должна быть равна дисбалансу сил, как показано стрелками. Этот дисбаланс сил представляет собой произведение внутреннего манометрического давления на площадь сопла. $F=AP$ —— ОБНОВЛЕНИЕ —— Основываясь на всех замечательных ответах и комментариях, я думаю, что следующий рисунок является лучшим представлением силы тяги. Внутреннее давление (красные стрелки) падает вблизи отверстия форсунки, поскольку скорость потока воды значительна. Кроме того, вода у отверстия форсунки не находится под нулевым давлением, как я предполагал изначально.
$\endgroup$ 6 $\begingroup$ Первый способ правильный. Во втором вы предположили, что давление в сопле по-прежнему равно $P$, несмотря на то, что вода выходит с некоторой скоростью. т. е. вы пренебрегли динамическим давлением. 92 = 2PA$$ $\endgroup$ 4 $\begingroup$ Часто эти ракеты запускаются с вертикального участка трубы или стержня, который проходит внутри бутылки, действуя как поршень до тех пор, пока ракета не продвинется достаточно далеко, чтобы пройти через конец трубы. Почему тяга должна увеличиваться при отделении ракеты от поршня? Позвольте мне попытаться предоставить интуитивное обоснование. Я не буду доказывать, что тяга удваивается, просто развею мнение, что она должна оставаться неизменной. Предположим, что поршень каким-то образом может расширяться, постоянно добавляя к себе маленькие цилиндрические заглушки. Эти заглушки изначально располагаются на высокой стойке рядом с ракетой; по мере того, как ракета движется вверх, поршень продолжает захватывать заглушку со стойки, каким-то образом транспортируя ее через стенку ракеты и добавляя ее на конец. Ракета никогда не покидает поршень, и понятно, что тяга остается всего лишь $PA$. Но это, по сути, то, что на самом деле происходит, когда ракета выбрасывает воду, за одним исключением. Каждый маленький кусочек воды, выходящий из сопла, можно рассматривать как «пробку», и сила, действующая, чтобы отделить его от остальной части ракеты, по-прежнему равна $PA$. Конечно, эта аналогия с пробками, добавляемыми во время полета, не соответствует реальному случаю ракеты, которая со временем теряет массу. Но эта разница не влияет на мгновенную тягу. $\endgroup$ $\begingroup$ Падение давления от давления в резервуаре до атмосферного давления не происходит мгновенно на сопле, а распределяется по площади канала потока. Это пониженное давление приводит к дополнительной тяге, которая не учитывалась во втором решении. Вот один из способов расчета этой дополнительной недостающей тяги: 92} \; dA $$ $$F = P_{бак} A_{выход} $$ Итак, во втором решении отсутствует $PA$. 1: Вы можете сделать свои уравнения более точными (особенно для ракет из тонкого баллона), используя реальную площадь поперечного сечения на поверхности воды вместо бесконечности как здесь, так и в пределе интеграла. $\endgroup$ $\begingroup$ Поскольку вы пренебрегли атмосферным давлением, давайте предположим, что вы проводите эксперимент в вакууме (я знаю, что где-то есть аналогия со сферической коровой 🙂 ). Вы предполагаете, что давление создается воздухом внутри баллона на поверхности. Воздух будет оказывать давление на пустую часть, как показано вашими стрелками, а также на горизонтальную поверхность воды. Теперь это будет отменено из-за полного цикла. Теперь, если бы воздушный шар был закрыт, результирующей силы не было бы, поскольку направленная вниз сила из-за давления воздуха была бы уравновешена нормальной силой. В вашем 1-м методе давление, которое вы измерили, — это давление воздуха внутри баллона. $\endgroup$ 3 $\begingroup$ Существует простое интуитивное объяснение фактора двойки. Тяга имеет два вклада, как показано ниже. 1) Давление воздуха в ракете воздействует на сопло F=PA точно так, как вы предположили во втором методе. 2) Выхлопная вода в момент выхода из сопла все еще находится под давлением и оказывает противодавление на ракету. Сила из-за противодавления также напрямую равна F=PA. Таким образом, комбинированный эффект равен 2PA. $\endgroup$ 8 Твой ответЗарегистрируйтесь или войдите в системуЗарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя адрес электронной почты и пароль Опубликовать как гостьЭлектронная почта Обязательно, но не отображается Опубликовать как гостьЭлектронная почта Требуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie Уравнение тяги газотурбинного двигателя
Калькулятор тяги двигателя | Расчет чистой тяги
👎 Формула Перезагрузить 👍 Чистая тяга силовой установкиШАГ 0: Итоги предварительного расчета ШАГ 1: Преобразование входных данных в базовые единицы Массовый расход воздуха: 0,9 кг в секунду —> 0,9 кг в секунду Преобразование не требуется ШАГ 2: вычисление формулы ШАГ 3: преобразование результата в единицу измерения 44. Суммирование приоритетов целей, которые необходимо максимизировать (Военные самолеты) Приоритет Сумма целей, которые необходимо максимизировать (%) = Приоритет производительности (%) + Приоритет качества полета (%) + Приоритет опасностей (%) + Приоритет ремонтопригодности (%) + Приоритет производительности (%) + Приоритет одноразовости (%) + Приоритет незаметности (%) Идти Приоритет объективного веса в процессе проектирования с учетом минимального расчетного индекса Приоритет веса (%) = ((Минимальный проектный индекс*100)-(Индекс затрат*Приоритет затрат (%))-(Индекс периода*Приоритет периода (%))))/Индекс веса Идти Приоритет объективной стоимости в процессе проектирования при минимальном расчетном показателе Приоритет затрат (%) = ((Минимальный проектный индекс*100)-(Индекс веса*Приоритет веса (%))-(Индекс периода*Приоритет периода (%))))/Индекс затрат Идти Приоритет целевого периода проектирования с учетом минимального расчетного индекса Приоритет периода (%) = ((Минимальный проектный индекс * 100) — (Индекс веса * Приоритет веса (%)) — (Индекс затрат * Приоритет затрат (%)))) / Индекс периода Идти Период расчетного индекса с учетом минимального расчетного индекса Индекс периода = ((Минимальный расчетный индекс * 100) — (Индекс веса * Приоритет веса (%)) — (Индекс затрат * Приоритет затрат (%)))) / Приоритет периода (%) Идти Индекс веса с учетом минимального расчетного индекса Индекс веса = ((Минимальный расчетный индекс * 100) — (Индекс затрат * Приоритет затрат (%)) — (Индекс периода * Приоритет периода (%)))) / Приоритет веса (%) Идти Индекс стоимости с учетом минимального расчетного индекса Индекс стоимости = ((Минимальный проектный индекс * 100) — (Индекс веса * Приоритет веса (%)) — (Индекс периода * Приоритет периода (%)))) / Приоритет затрат (%) Идти Минимальный расчетный индекс Минимальный проектный индекс = ((Индекс затрат * Приоритет затрат (%)) + (Индекс веса * Приоритет веса (%)) + (Индекс периода * Приоритет периода (%))))/100 Идти Суммирование приоритетов всех целей, которые необходимо минимизировать Приоритет Сумма целей, которые необходимо минимизировать (%) = Приоритет затрат (%) + Приоритет веса (%) + Приоритет периода (%) Идти Чистая тяга двигателя Сила тяги = Массовый расход воздуха * (скорость реактивного полета) Идти Формула чистой тяги двигателя Сила тяги = Массовый расход воздуха * (скорость реактивного полета) Что такое реактивное движение? Реактивное движение — это движение объекта в одном направлении, производимое выбросом струи жидкости в противоположном направлении. Как рассчитать чистую тягу движущей силы?Калькулятор чистой тяги движителя использует Сила тяги = Массовый расход воздуха * (скорость реактивного полета) для расчета силы тяги, уравнение чистой тяги движителя показывает, что чистая тяга равна полной тяге минус прямое сопротивление. Сила тяги обозначается символом Ft . Как рассчитать реактивную тягу с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для чистой тяги, введите массовый расход воздуха (m af ) , скорость струи (V) и скорость полета (V f ) и нажмите кнопку расчета. Вот как можно объяснить расчет чистой тяги движителя с заданными входными значениями -> 44,46 = 0,9*(50-0,6) . Часто задаваемые вопросыЧто такое тяга силовой установки? Сила тяги Уравнение чистой тяги показывает, что чистая тяга равна полной тяге минус лобовое сопротивление и представляется как Ft = m af *(V-V f ) скорость полета) . Как рассчитать реактивную тягу? Сила тяги Уравнение чистой тяги показывает, что чистая тяга равна полной тяге минус прямое сопротивление, вычисляемое с использованием Сила тяги = Массовый расход воздуха*(скорость реактивного полета) . Чтобы рассчитать чистую тягу движителя, вам потребуется массовый расход воздуха (m af ) , скорость струи (V) и скорость полета (V f ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для массового расхода воздуха, скорости струи и скорости полета и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода. Поделиться Скопировано! Тяга — AviationChief. Com ComВ аэродинамике мы беспокоимся о тяге, потому что она является ключевым фактором характеристик самолета. Хотя вы можете измерить тягу реактивного двигателя на испытательном стенде, как показано выше с двигателем J-58 от SR-71, измерения в кабине, такие как ЭПР , используются больше для относительных измерений. «Двигайтесь вперед, летите быстрее» и т. д. Мы углубимся в тему тяги, чтобы понять характеристики самолета на разных скоростях и узнать, как добиться максимальной дальности полета или выносливости вашего корабля. Прежде чем мы начнем, позвольте мне признать, что производительность турбовентилятора отличается от работы прямого турбореактивного двигателя. При рассмотрении турбовентилятора я сделал несколько предположений, чтобы упростить задачу. Большая часть теории взята с самолета ВВС США Т-38А с двигателями J85-GE-5. С учетом турбовентилятора
Принципы движения Вы можете резюмировать принцип работы реактивного двигателя с помощью двух принципов, предложенных вам сэром Исааком Ньютоном. Второй закон движения Ньютона можно записать так: F=maF=ma Сила F, действующая на массу a, заставит массу ускоряться в направлении действия силы. Масса – это воздух, проходящий через реактивный двигатель. Третий закон движения Ньютона гласит, что для каждой силы действия существует равная и противоположно направленная сила противодействия. Сила действия – это частицы воздуха, ускоряющиеся назад, сила реакции – на сам двигатель, ускоряющийся вперед. Мы можем вывести уравнение для тяги в реактивном двигателе с помощью небольшой математической ловкости рук, манипулируя проверенными уравнениями, чтобы получить единицы измерения силы, которые можно измерить в фунтах. Из наших рассуждений о массе мы знаем, что в английской системе единицами измерения массы являются фунт-сек2/фут, также известный как пуля . Принципы движения Из уравнения непрерывности мы знаем, что: это на секунду дает в результате фунт-сек / фут. Тяга: F=T=Q(V2−V1) Q = массовый расход воздуха = ρAV (слагов/с) V1 = скорость на входе (полет) (фут/с) V2 = скорость на выходе (фут/с) масса воздушного потока, проходящего через двигатель, или разница скорости на выходе и на входе этого воздушного потока. Хотя увеличение выходной скорости кажется отличным решением, это будет означать превращение реактивного топлива в кинетическую энергию, которая будет потеряна в атмосфере, как только она выйдет из выхлопной трубы. Действительно, самый эффективный реактивный двигатель имел бы скорость на выходе, почти равную скорости на входе, но при этом перемещалось бы очень большое количество воздуха. Повышение m более эффективно, чем повышение (V2 – V1). Отсюда тенденция к увеличению размеров всасывающих вентиляторов реактивных двигателей. Кривая требуемой тяги Измерить тягу реактивного двигателя в полете чрезвычайно сложно. Обычно они устанавливаются на испытательном стенде, ограничиваются от перемещения и подключаются к датчику силы. В результате получается статических тяговых. К счастью, гораздо проще измерить сопротивление в аэродинамической трубе. Кривая сопротивления Т-38 Как видно из двух графиков, графики одинаковы для горизонтального полета без ускорения. Тяга = сопротивление, в конце концов. Требуемая тяга Т-38 Кривые доступной тяги/требуемой тяги Если добавить доступную тягу к диаграмме требуемой тяги, можно экстраполировать некоторые характеристики. Например, показанная диаграмма уровня моря показывает, где находится максимальная скорость Т-38 по сравнению с двумя настройками мощности. Т-38 Тяга-Имеющаяся/Требуемая тяга Влияние высоты на тягу-Доступная/Требуемая тяга Кривая Хотя очевидно, что доступная тяга будет уменьшаться с высотой, влияние на требуемую тягу менее очевидно. D=CDqS D Влияние высоты на доступную/требуемую тягу Т-38 Влияние веса на кривые требуемой тяги аэродинамическая сила должна компенсироваться, и для этого необходимая тяга должна увеличиваться. Чистый эффект заключается в том, что увеличение веса имеет тенденцию сдвигать кривую требуемой тяги вверх и вправо. Это интуитивно понятно: увеличение веса сужает диапазон скоростей и увеличивает минимальную скорость, но в то же время требует большей тяги. Влияние веса Т-38 на требуемую тягу Влияние конфигурации на кривые требуемой тяги Изменение конфигурации во многом противоположно изменению веса. Опускание шасси или выпуск закрылков значительно увеличивает паразитное сопротивление, оказывая относительно меньшее влияние на индуктивное сопротивление. В результате кривая требуемой тяги смещается вверх и влево. Влияние конфигурации Т-38 на требуемую тягу L/D МАКС. Типичное отношение подъемной силы к лобовому сопротивлению Глядя на диаграмму требуемой тяги самолета, мы видим ту же точку, но на этот раз в надире кривой. В L/DMAX AOA происходят четыре важных момента:
T-38 L/D MAX Максимальная дальность Определение воздушной скорости, обеспечивающей максимальную дальность полета, требует небольшой тригонометрии:0011 Range=морские милиlbsRange=морские милиlbsДеление обеих сторон дроби на время: Range=морские мили/часlbs/hourRange=морские мили/часlbs/часУдаление единиц измерения: RangeMAX происходит при (Расход топлива / V)MIN Отношения расхода топлива к скорости образуют треугольник на диаграмме требуемой тяги, как показано θ1 и θ2. Отношение Расход топлива/V минимизируется, когда минимизируется тангенс θ. Эту точку можно найти, начертив графически линию от начала координат до требуемой кривой тяги. Максимальная дальность Т-38 Влияние веса на максимальную дальность Как мы видели при рассмотрении влияния веса на требуемую тягу, увеличение веса сдвигает кривую требуемой тяги вверх и вправо. Однако большее значение при обсуждении диапазона имеет то, что происходит при уменьшении веса. Кривые переключаются вниз и влево, что означает, что воздушная скорость должна уменьшаться по мере выгорания топлива для достижения максимальной дальности. Влияние веса Т-38 на максимальную дальность Влияние высоты на дальность более низкая температура вверх через тропопаузу и увеличение оборотов двигателя до более эффективных диапазонов. Вероятно, это справедливо для большинства самолетов. Влияние высоты Т-38 на дальность Влияние ветра на дальность Следующее может быть верным для Т-38: «Самолет, летящий против встречного ветра, находится в неблагоприятных условиях и, следовательно, должен лететь с более высокой истинной воздушной скоростью, чтобы уменьшить эффект встречного ветра. Прилагаемая диаграмма для Т-38, кажется, подтверждает это, регулировка скорости по ветру, похоже, указывает другую касательную к требуемой линии тяги. Как мы видели выше, линия, проведенная от начала координат до кривой, указывает скорость, при которой диапазон максимален. Таким образом, теория заключается в том, что вы можете настроить начало координат, чтобы учесть ветер. Проверка теории Используя диаграммы производительности 1T-38A-1, мы можем проверить это утверждение, используя самолет массой 10 000 фунтов, летящий на высоте 25 000 футов, и определить, что MMaximum Range = 0,75. где TAS = 450 и расход топлива = 1700 фунтов/час. При отсутствии ветра дальность полета на 1000 фунтов топлива составляет 450 (нм/ч) x (1000 фунтов) / (1700 фунтов/ч) = 265 морских миль. При столкновении со встречным ветром 40 узлов дальность уменьшается до (450 — 40) (морских миль/час) x (1000 фунтов) / (1700 фунтов/час) = 241 морских миль. Если теория подтвердится, мы увеличим дальность полета на 1000 фунтов топлива, если наберем скорость. Разгоняясь до М 0,80, мы видим TAS = 49.0 TAS и расход топлива = 2000 фунтов/ч. При том же встречном ветре наш диапазон составляет (490 — 40) (морских миль/час) x (1000 фунтов) / 2000 фунтов/час) = 225 морских миль. Меньше! Как насчет попутного ветра? При столкновении с попутным ветром в 40 узлов наша производительность M 0,75 становится равной 450 + 40) (морских миль/час) x (1000 фунтов) / (1700 фунтов/час) = 288 морских миль. Согласно теории, наша 1000-фунтовая дальность полета увеличится, если мы снизим скорость. Замедляясь до M 0,70, мы видим TAS = 4420 TAS и расход топлива = 1600 фунтов/час. При том же встречном ветре наш диапазон составляет (420 + 40) (морских миль/час) x (1000 фунтов) / 1600 фунтов/час) = 287 морских миль. Близко, но все же меньше! Хотя это всего лишь одна точка данных, похоже, что утверждение для Т-38 ложно. Примечание. 2019 © Все права защищены. Карта сайта |



 Удельный импульс часто используется для определения того, насколько хорошо двигатель создает тягу . Этот параметр жизненно важен для сравнения характеристик двигателей различных классов , так как он является только функцией развиваемой тяги и скорости выхлопа или массового расхода.
Удельный импульс часто используется для определения того, насколько хорошо двигатель создает тягу . Этот параметр жизненно важен для сравнения характеристик двигателей различных классов , так как он является только функцией развиваемой тяги и скорости выхлопа или массового расхода.  В основном, массы топлива расходуется в единицу времени для достижения единицы тяги . Термин тягоспецифический означает, что этот параметр можно назвать расходом топлива по отношению к единице тяги. Измеряется в граммах топлива в секунду-килоньютонах тяги, г/(с⋅кН)\text{г/(с}\cdot\text{кН)}г/(с⋅кН) или фунтах топлива на час-фунт тяги фунт/(ч⋅фунт-сила)\text{фунт/(ч}\cdot\text{фунт-сила)}фунт/(ч⋅фунт-сила) в имперских единицах. Математически это:
В основном, массы топлива расходуется в единицу времени для достижения единицы тяги . Термин тягоспецифический означает, что этот параметр можно назвать расходом топлива по отношению к единице тяги. Измеряется в граммах топлива в секунду-килоньютонах тяги, г/(с⋅кН)\text{г/(с}\cdot\text{кН)}г/(с⋅кН) или фунтах топлива на час-фунт тяги фунт/(ч⋅фунт-сила)\text{фунт/(ч}\cdot\text{фунт-сила)}фунт/(ч⋅фунт-сила) в имперских единицах. Математически это:
 80665=2070 s\quad \ \ \ \small I_{sp} = \frac{v_e}{g_0} = \frac{20000}{9.80665} = 2070 \text{ s} Isp=g0 ve=9.8066520000=2070 с
80665=2070 s\quad \ \ \ \small I_{sp} = \frac{v_e}{g_0} = \frac{20000}{9.80665} = 2070 \text{ s} Isp=g0 ve=9.8066520000=2070 с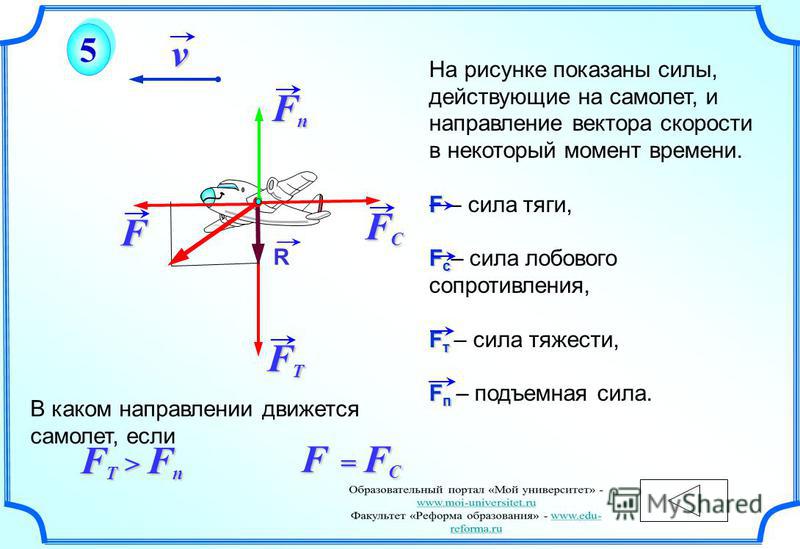

 Также необходимо максимально снизить давление газа внутри сопла за счет создания большого коэффициента сечения. Коэффициент сечения или коэффициент расширения определяется как площадь выхода A e разделить на площадь горловины A t .
Также необходимо максимально снизить давление газа внутри сопла за счет создания большого коэффициента сечения. Коэффициент сечения или коэффициент расширения определяется как площадь выхода A e разделить на площадь горловины A t . То есть,
То есть,
 Поскольку dM/dt , изменение массы тела во времени, в этом случае отрицательно, то в пределе величина M/t заменяется на — dM/dt . Количество u-(v+v) равно V rel , относительная скорость выбрасываемой массы по отношению к ракете. С учетом этих изменений уравнение (1.4) можно записать в виде
Поскольку dM/dt , изменение массы тела во времени, в этом случае отрицательно, то в пределе величина M/t заменяется на — dM/dt . Количество u-(v+v) равно V rel , относительная скорость выбрасываемой массы по отношению к ракете. С учетом этих изменений уравнение (1.4) можно записать в виде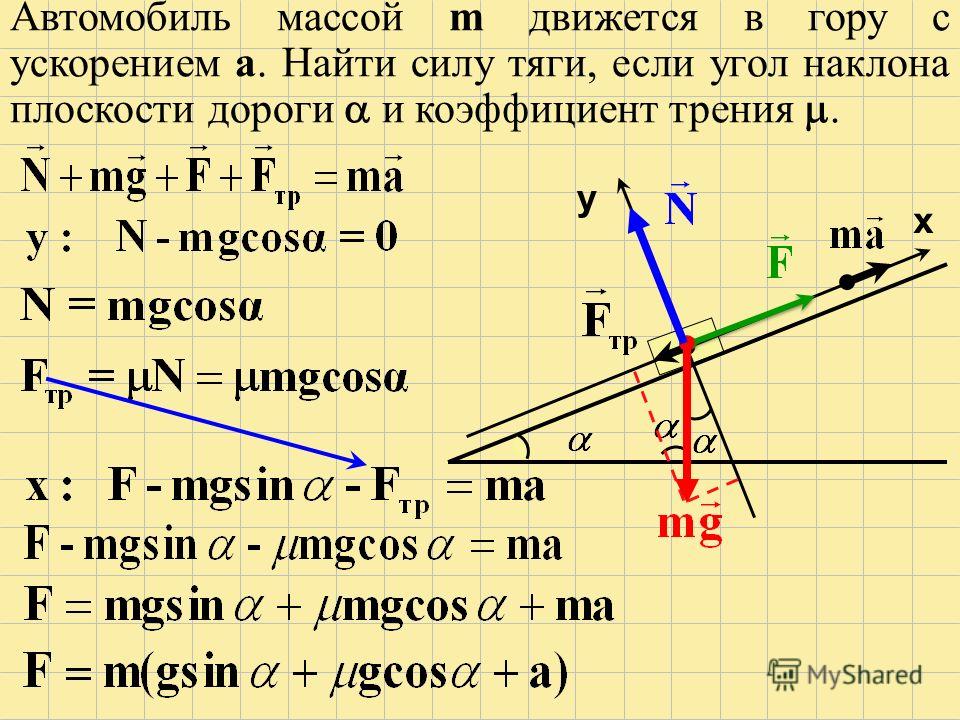 Произведение qV e , которое мы получили выше ( V rel × dM/dt ), называется импульсом или скоростью тяги. Произведение (P e -P a )A e , называемое тягой давления, является результатом неуравновешенных сил давления на выходе из сопла. Как мы увидим позже, максимальная тяга возникает, когда P e = P a .
Произведение qV e , которое мы получили выше ( V rel × dM/dt ), называется импульсом или скоростью тяги. Произведение (P e -P a )A e , называемое тягой давления, является результатом неуравновешенных сил давления на выходе из сопла. Как мы увидим позже, максимальная тяга возникает, когда P e = P a . Уравнение выражает, что когда на частицу действует сила 90 245 F 90 246 в течение заданного интервала времени, конечный импульс p 2 частицы можно получить, сложив ее начальный импульс p 1 и импульс силы F за интервал времени.
Уравнение выражает, что когда на частицу действует сила 90 245 F 90 246 в течение заданного интервала времени, конечный импульс p 2 частицы можно получить, сложив ее начальный импульс p 1 и импульс силы F за интервал времени. В час т , масса корпуса ракеты и остатка топлива M-qt , скорость v . За интервал времени t выбрасывается масса топлива qt . Обозначая через u абсолютную скорость выброшенного топлива, мы применяем принцип импульса и импульса между временем t и временем t+t . Обратите внимание, что этот вывод не учитывает влияние сопротивления воздуха.
В час т , масса корпуса ракеты и остатка топлива M-qt , скорость v . За интервал времени t выбрасывается масса топлива qt . Обозначая через u абсолютную скорость выброшенного топлива, мы применяем принцип импульса и импульса между временем t и временем t+t . Обратите внимание, что этот вывод не учитывает влияние сопротивления воздуха. Более того, результирующую скорость правильнее выражать как изменение скорости или V. Таким образом, уравнение (1.15) принимает вид
Более того, результирующую скорость правильнее выражать как изменение скорости или V. Таким образом, уравнение (1.15) принимает вид
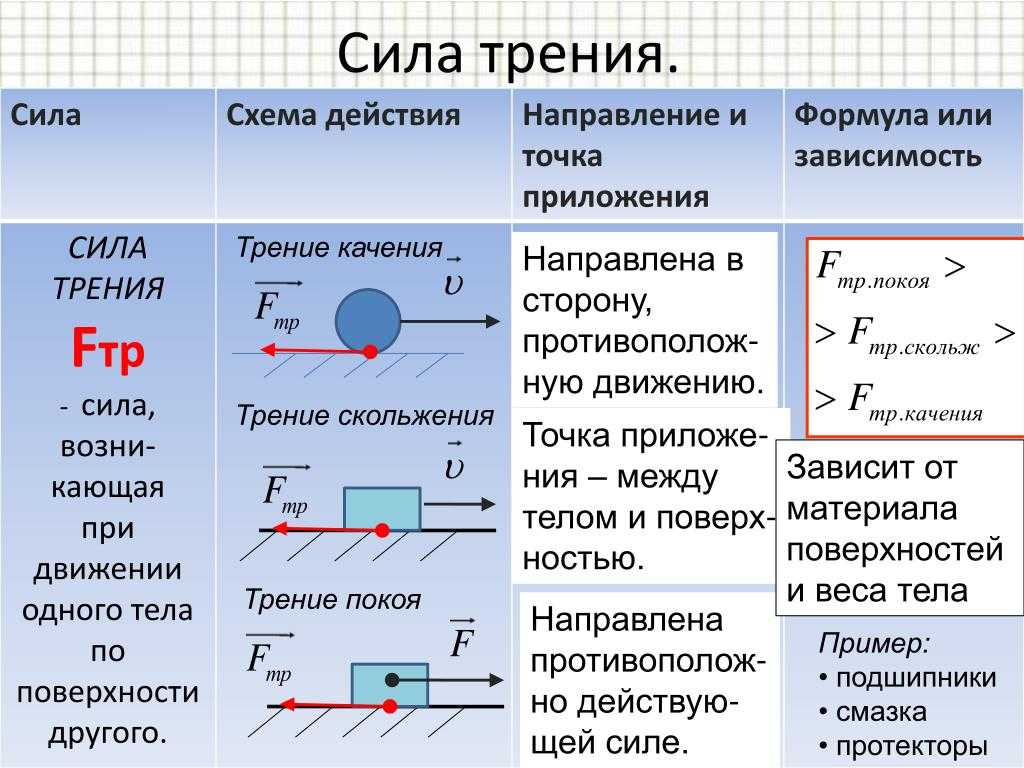
 Для автомобиля с ограниченным объемом, работающего на топливе с низкой плотностью, таком как жидкий водород, можно добиться значительного уменьшения размеров автомобиля путем перехода к более высокому соотношению O/F. В этом случае потери производительности с лихвой компенсируются уменьшением потребности в топливном баке. Также рассмотрим пример двухтопливных систем с использованием NTO/MMH, где соотношение смеси 1,67 приводит к тому, что топливный и окислительный баки имеют одинаковый размер. Равные размеры упрощают изготовление резервуаров, компоновку системы и интеграцию.
Для автомобиля с ограниченным объемом, работающего на топливе с низкой плотностью, таком как жидкий водород, можно добиться значительного уменьшения размеров автомобиля путем перехода к более высокому соотношению O/F. В этом случае потери производительности с лихвой компенсируются уменьшением потребности в топливном баке. Также рассмотрим пример двухтопливных систем с использованием NTO/MMH, где соотношение смеси 1,67 приводит к тому, что топливный и окислительный баки имеют одинаковый размер. Равные размеры упрощают изготовление резервуаров, компоновку системы и интеграцию.
 То есть высокая теплота сгорания вызывает разделение молекул на более простые составляющие, которые затем способны к рекомбинации. Рассмотрим реакцию керосина с кислородом. Истинные продукты сгорания будут представлять собой равновесную смесь атомов и молекул, состоящую из C, CO, CO 2 , H, H 2 , H 2 O, HO, O и O 2 . Диссоциация оказывает существенное влияние на температуру пламени.
То есть высокая теплота сгорания вызывает разделение молекул на более простые составляющие, которые затем способны к рекомбинации. Рассмотрим реакцию керосина с кислородом. Истинные продукты сгорания будут представлять собой равновесную смесь атомов и молекул, состоящую из C, CO, CO 2 , H, H 2 , H 2 O, HO, O и O 2 . Диссоциация оказывает существенное влияние на температуру пламени. Таким образом, бензин обычно считается октановым числом C 8 H 18 , а керосин считается додеканом C 12 H 26 .
Таким образом, бензин обычно считается октановым числом C 8 H 18 , а керосин считается додеканом C 12 H 26 .
 24) очень полезно при решении уравнений (1.18)–(1.21). Нам редко дают прямое значение C , однако удельный импульс ракетного двигателя является общепринятым параметром, из которого мы можем легко вычислить C .
24) очень полезно при решении уравнений (1.18)–(1.21). Нам редко дают прямое значение C , однако удельный импульс ракетного двигателя является общепринятым параметром, из которого мы можем легко вычислить C . Камера должна быть достаточно прочной, чтобы выдерживать высокое давление, создаваемое процессом сгорания, и высокую температуру, возникающую в результате процесса горения. Из-за высокой температуры и теплопередачи камера и сопло обычно охлаждаются. Камера также должна быть достаточной длины, чтобы обеспечить полное сгорание до того, как газы поступят в сопло.
Камера должна быть достаточно прочной, чтобы выдерживать высокое давление, создаваемое процессом сгорания, и высокую температуру, возникающую в результате процесса горения. Из-за высокой температуры и теплопередачи камера и сопло обычно охлаждаются. Камера также должна быть достаточной длины, чтобы обеспечить полное сгорание до того, как газы поступят в сопло. Сопло обычно делают достаточно длинным (или с достаточно большой площадью выходного сечения), чтобы давление в камере сгорания на выходе из сопла уменьшалось до давления, существующего вне сопла. Именно при таком условии P e = P a , где P e — давление на выходе из сопла, а P a — внешнее атмосферное давление, которое является максимальным, и сопло считается адаптированным. , также называемое оптимальным или правильным расширением. Когда P e больше, чем P a , сопло недостаточно выдвинуто. Когда верно обратное, оно чрезмерно растянуто.
Сопло обычно делают достаточно длинным (или с достаточно большой площадью выходного сечения), чтобы давление в камере сгорания на выходе из сопла уменьшалось до давления, существующего вне сопла. Именно при таком условии P e = P a , где P e — давление на выходе из сопла, а P a — внешнее атмосферное давление, которое является максимальным, и сопло считается адаптированным. , также называемое оптимальным или правильным расширением. Когда P e больше, чем P a , сопло недостаточно выдвинуто. Когда верно обратное, оно чрезмерно растянуто.
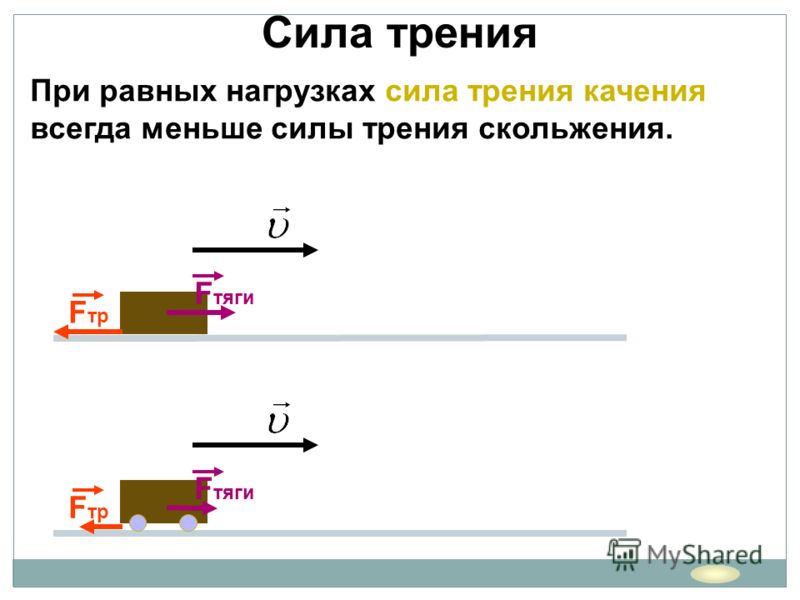 Эта область затем будет областью выхода сопла.
Эта область затем будет областью выхода сопла. Это особенно верно для ступеней, отличных от первой, где диаметр сопла не может быть больше, чем внешний диаметр ступени ниже. Для космических двигателей, где давление окружающей среды равно нулю, тяга всегда увеличивается с увеличением степени расширения сопла. На этих двигателях коэффициент расширения сопла обычно увеличивается до тех пор, пока дополнительный вес более длинного сопла не будет стоить больше производительности, чем создаваемая им дополнительная тяга.
Это особенно верно для ступеней, отличных от первой, где диаметр сопла не может быть больше, чем внешний диаметр ступени ниже. Для космических двигателей, где давление окружающей среды равно нулю, тяга всегда увеличивается с увеличением степени расширения сопла. На этих двигателях коэффициент расширения сопла обычно увеличивается до тех пор, пока дополнительный вес более длинного сопла не будет стоить больше производительности, чем создаваемая им дополнительная тяга.
 Этот коэффициент (эффективность тяги) представляет собой отношение импульса выходящего газа конического сопла к импульсу идеального сопла с равномерным параллельным осевым потоком газа. Значение может быть выражено следующим уравнением:
Этот коэффициент (эффективность тяги) представляет собой отношение импульса выходящего газа конического сопла к импульсу идеального сопла с равномерным параллельным осевым потоком газа. Значение может быть выражено следующим уравнением: Длина раструбного патрубка более 80 % не оказывает значительного влияния на производительность, особенно с учетом потери веса. Тем не менее, длина патрубка до 100 % может быть оптимальной для применений, требующих очень высокой производительности.
Длина раструбного патрубка более 80 % не оказывает значительного влияния на производительность, особенно с учетом потери веса. Тем не менее, длина патрубка до 100 % может быть оптимальной для применений, требующих очень высокой производительности. Стеновые углы n и e показаны на рисунке 1.6 в зависимости от коэффициента расширения. Оптимальные контуры сопла могут быть очень точно аппроксимированы путем выбора соответствующих входных данных. Хотя не делается никаких поправок на различные комбинации топлив, опыт показал лишь незначительное влияние коэффициента теплоемкости на контур.
Стеновые углы n и e показаны на рисунке 1.6 в зависимости от коэффициента расширения. Оптимальные контуры сопла могут быть очень точно аппроксимированы путем выбора соответствующих входных данных. Хотя не делается никаких поправок на различные комбинации топлив, опыт показал лишь незначительное влияние коэффициента теплоемкости на контур.
 Типичные значения L* для различных порохов показаны в таблице ниже. Установив площадь горловины и требуемый минимум л*, объем камеры можно рассчитать по уравнению (1.33).
Типичные значения L* для различных порохов показаны в таблице ниже. Установив площадь горловины и требуемый минимум л*, объем камеры можно рассчитать по уравнению (1.33).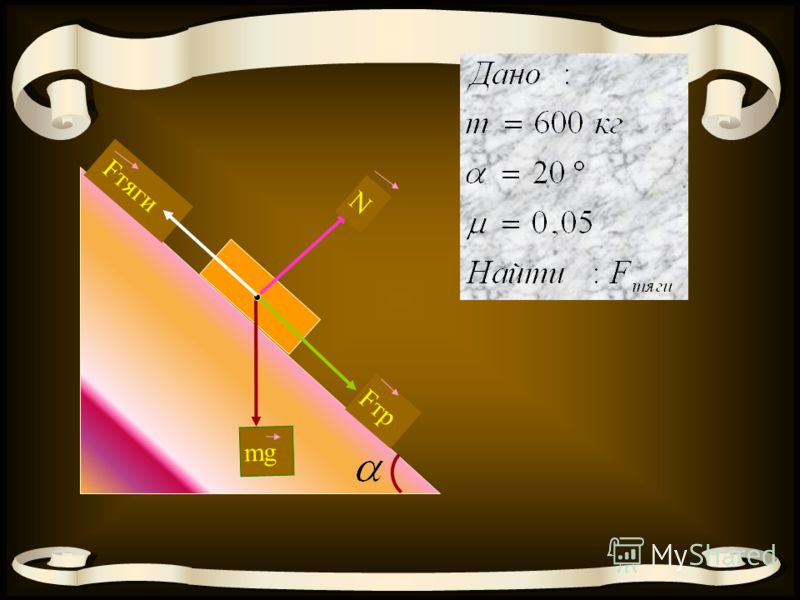
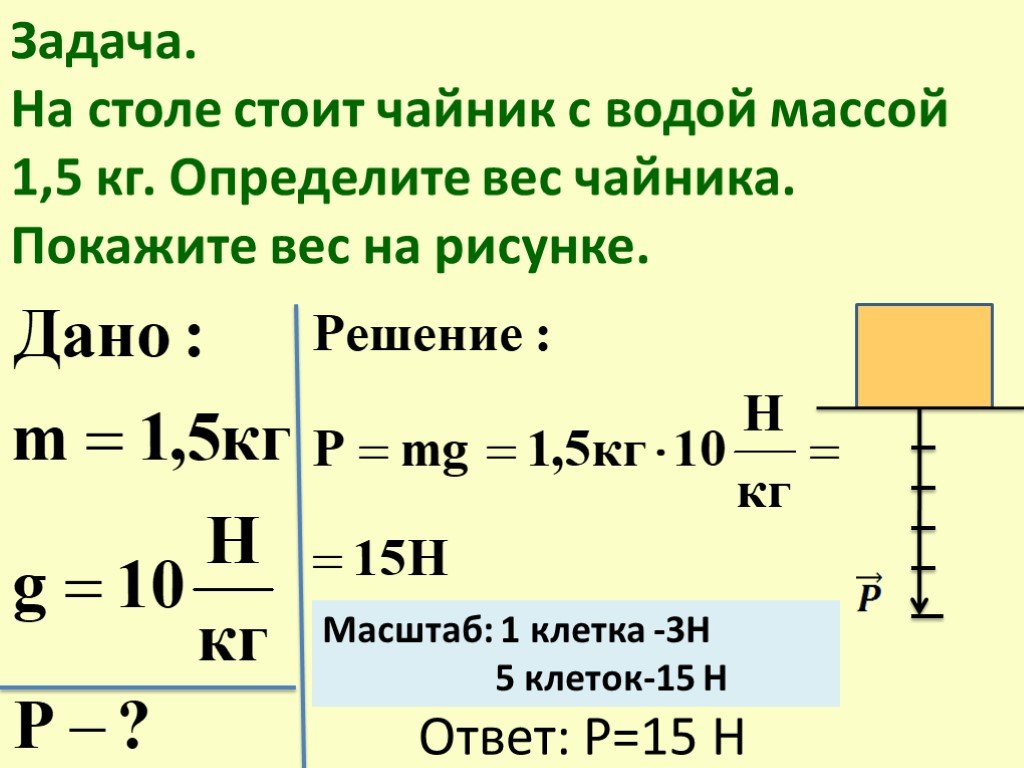
 34), получаем следующее, которое можно решить для диаметра камеры путем итерации:
34), получаем следующее, которое можно решить для диаметра камеры путем итерации:
 Локальное перемешивание в пределах формы распыления элемента впрыска должно происходить практически на микроскопическом уровне, чтобы обеспечить эффективность сгорания, приближающуюся к 100%.
Локальное перемешивание в пределах формы распыления элемента впрыска должно происходить практически на микроскопическом уровне, чтобы обеспечить эффективность сгорания, приближающуюся к 100%.
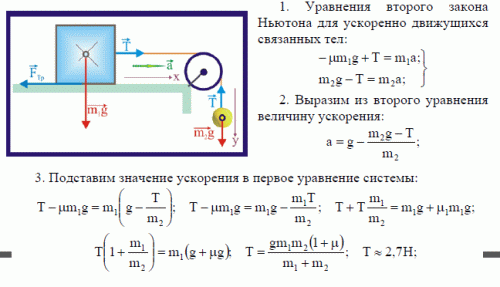 Таким образом, цикл подходит для умеренных требований к мощности, но не для систем большой мощности, которым пришлось бы отводить большую часть основного потока на менее эффективный поток газогенератора.
Таким образом, цикл подходит для умеренных требований к мощности, но не для систем большой мощности, которым пришлось бы отводить большую часть основного потока на менее эффективный поток газогенератора. Преимущество по сравнению с газогенераторным циклом состоит в том, что все топливо сжигается при оптимальном соотношении смеси в основной камере и поток не сбрасывается за борт. Ступенчатый цикл сгорания часто используется для приложений большой мощности. Чем выше давление в камере, тем меньше и легче может быть двигатель для создания такой же тяги. Стоимость разработки для этого цикла выше, поскольку высокое давление усложняет процесс разработки. Другими недостатками являются жесткие условия работы турбины, высокотемпературные трубопроводы, необходимые для подачи горячих газов, и очень сложная конструкция обратной связи и управления.
Преимущество по сравнению с газогенераторным циклом состоит в том, что все топливо сжигается при оптимальном соотношении смеси в основной камере и поток не сбрасывается за борт. Ступенчатый цикл сгорания часто используется для приложений большой мощности. Чем выше давление в камере, тем меньше и легче может быть двигатель для создания такой же тяги. Стоимость разработки для этого цикла выше, поскольку высокое давление усложняет процесс разработки. Другими недостатками являются жесткие условия работы турбины, высокотемпературные трубопроводы, необходимые для подачи горячих газов, и очень сложная конструкция обратной связи и управления. Затем пары топлива проходят через турбину и впрыскиваются в основную камеру для сгорания вместе с окислителем. Этот цикл работает с такими видами топлива, как водород или метан, которые имеют низкую температуру кипения и легко испаряются. Как и в случае ступенчатого цикла сгорания, все топливо сжигается при оптимальном соотношении смеси в основной камере, и обычно поток не сбрасывается за борт; однако передача тепла топливу ограничивает мощность, доступную для турбины, что делает этот цикл подходящим для двигателей малого и среднего размера. Разновидностью системы является открытый или продувочный цикл детандера, в котором для привода турбины используется только часть топлива. В этом варианте выхлоп турбины сбрасывается за борт до давления окружающей среды, чтобы увеличить степень сжатия турбины и выходную мощность. Это может обеспечить более высокое давление в камере, чем замкнутый расширительный цикл, хотя и с меньшей эффективностью из-за потока за бортом.
Затем пары топлива проходят через турбину и впрыскиваются в основную камеру для сгорания вместе с окислителем. Этот цикл работает с такими видами топлива, как водород или метан, которые имеют низкую температуру кипения и легко испаряются. Как и в случае ступенчатого цикла сгорания, все топливо сжигается при оптимальном соотношении смеси в основной камере, и обычно поток не сбрасывается за борт; однако передача тепла топливу ограничивает мощность, доступную для турбины, что делает этот цикл подходящим для двигателей малого и среднего размера. Разновидностью системы является открытый или продувочный цикл детандера, в котором для привода турбины используется только часть топлива. В этом варианте выхлоп турбины сбрасывается за борт до давления окружающей среды, чтобы увеличить степень сжатия турбины и выходную мощность. Это может обеспечить более высокое давление в камере, чем замкнутый расширительный цикл, хотя и с меньшей эффективностью из-за потока за бортом. На практике цикл ограничен относительно низким давлением в камере, потому что более высокое давление делает баки транспортного средства слишком тяжелыми. Цикл может быть надежным, учитывая его меньшее количество деталей и сложность по сравнению с другими системами.
На практике цикл ограничен относительно низким давлением в камере, потому что более высокое давление делает баки транспортного средства слишком тяжелыми. Цикл может быть надежным, учитывая его меньшее количество деталей и сложность по сравнению с другими системами. Для решения этой задачи успешно используются несколько методов камерного охлаждения. Выбор оптимального метода охлаждения камеры тяги зависит от многих соображений, таких как тип топлива, давление в камере, доступное давление охлаждающей жидкости, конфигурация камеры сгорания и материал камеры сгорания.
Для решения этой задачи успешно используются несколько методов камерного охлаждения. Выбор оптимального метода охлаждения камеры тяги зависит от многих соображений, таких как тип топлива, давление в камере, доступное давление охлаждающей жидкости, конфигурация камеры сгорания и материал камеры сгорания. Однако для последующих применений ракетных двигателей давление в камере было увеличено, и стало труднее удовлетворить требования к охлаждению. Возникла необходимость в разработке новых схем теплоносителя, более эффективных конструктивно и с улучшенными теплообменными характеристиками.
Однако для последующих применений ракетных двигателей давление в камере было увеличено, и стало труднее удовлетворить требования к охлаждению. Возникла необходимость в разработке новых схем теплоносителя, более эффективных конструктивно и с улучшенными теплообменными характеристиками. Ярким примером камеры сгорания с канальной стенкой является SSME, который работает при номинальном давлении в камере 204 атмосферы при температуре 3600 K в течение 520 секунд. Теплопередача и структурные характеристики превосходны.
Ярким примером камеры сгорания с канальной стенкой является SSME, который работает при номинальном давлении в камере 204 атмосферы при температуре 3600 K в течение 520 секунд. Теплопередача и структурные характеристики превосходны. Этот метод имеет ограниченное применение из-за потери производительности в результате сброса охлаждающей жидкости за борт. На сегодняшний день охлаждение дампа в реальных приложениях не использовалось.
Этот метод имеет ограниченное применение из-за потери производительности в результате сброса охлаждающей жидкости за борт. На сегодняшний день охлаждение дампа в реальных приложениях не использовалось. В результате относительно холодные газы обтекают поверхность стенки, снижая тем самым температуру пограничного слоя и способствуя процессу охлаждения.
В результате относительно холодные газы обтекают поверхность стенки, снижая тем самым температуру пограничного слоя и способствуя процессу охлаждения. В космической отрасли используются два основных типа твердотопливных блоков. Это цилиндрические блоки с горением спереди или на поверхности и цилиндрические блоки с внутренним сгоранием. В первом случае фронт пламени распространяется слоями от соплового конца блока к верхней части кожуха. Эта так называемая торцевая горелка создает постоянную тягу на протяжении всего горения. Во втором, более обычном случае, поверхность горения развивается по длине центрального канала. Иногда канал имеет форму звезды или другую геометрию для сдерживания роста этой поверхности.
В космической отрасли используются два основных типа твердотопливных блоков. Это цилиндрические блоки с горением спереди или на поверхности и цилиндрические блоки с внутренним сгоранием. В первом случае фронт пламени распространяется слоями от соплового конца блока к верхней части кожуха. Эта так называемая торцевая горелка создает постоянную тягу на протяжении всего горения. Во втором, более обычном случае, поверхность горения развивается по длине центрального канала. Иногда канал имеет форму звезды или другую геометрию для сдерживания роста этой поверхности. Те, у которых есть канал, а также центральный цилиндр топлива (2), создают относительно постоянную тягу, которая очень быстро уменьшается до нуля, когда топливо израсходовано. Профиль пятиконечной звезды (3) развивает относительно постоянную тягу, которая медленно уменьшается до нуля по мере расходования последнего топлива. Крестообразный профиль (4) создает прогрессивно меньшую тягу. Топливо в блоке с профилем «двойной якорь» (5) создает уменьшающуюся тягу, которая быстро падает ближе к концу горения. Профиль «зубчатый» (6) создает сильную начальную тягу, за которой следует почти постоянная нижняя тяга.
Те, у которых есть канал, а также центральный цилиндр топлива (2), создают относительно постоянную тягу, которая очень быстро уменьшается до нуля, когда топливо израсходовано. Профиль пятиконечной звезды (3) развивает относительно постоянную тягу, которая медленно уменьшается до нуля по мере расходования последнего топлива. Крестообразный профиль (4) создает прогрессивно меньшую тягу. Топливо в блоке с профилем «двойной якорь» (5) создает уменьшающуюся тягу, которая быстро падает ближе к концу горения. Профиль «зубчатый» (6) создает сильную начальную тягу, за которой следует почти постоянная нижняя тяга.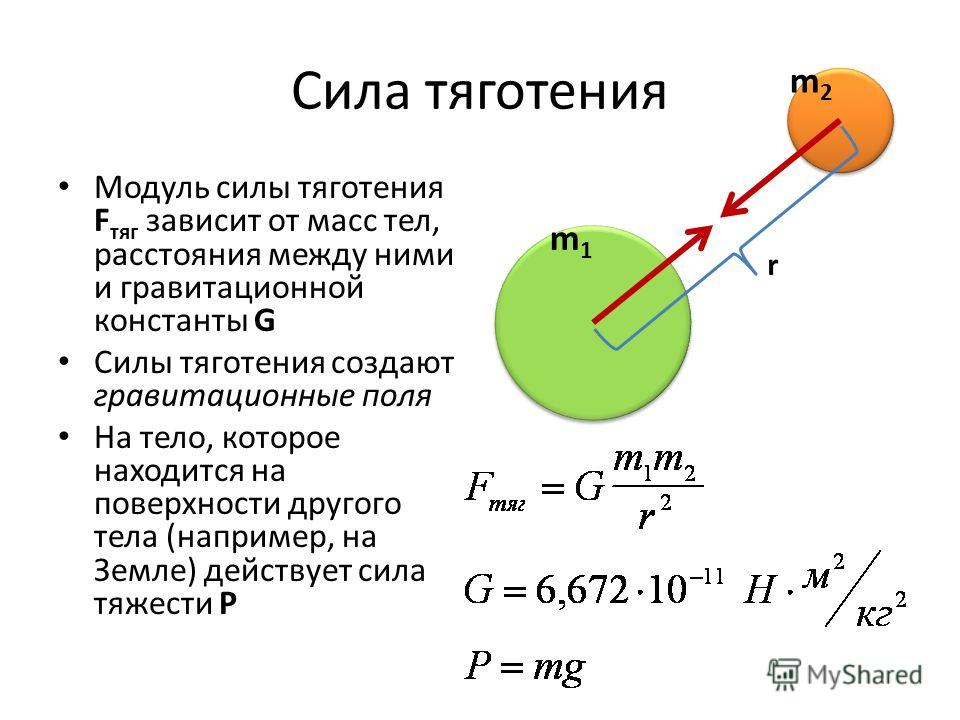 Количественное знание скорости горения топлива и того, как она изменяется в различных условиях, имеет фундаментальное значение для успешного проектирования твердотопливного двигателя.
Количественное знание скорости горения топлива и того, как она изменяется в различных условиях, имеет фундаментальное значение для успешного проектирования твердотопливного двигателя. Важно понимать, что один набор значений a, n обычно действителен в определенном диапазоне давлений. Для точного представления интересующего режима полного давления может потребоваться более одного набора.
Важно понимать, что один набор значений a, n обычно действителен в определенном диапазоне давлений. Для точного представления интересующего режима полного давления может потребоваться более одного набора.
 Для зерна с большим отношением L/D следует использовать большее соотношение A port /A t .
Для зерна с большим отношением L/D следует использовать большее соотношение A port /A t . Например, если кто-то хочет сконструировать зерно с торцевой горелкой, которое имеет относительно небольшую площадь горения, необходимо иметь быстрогорящее топливо. В других обстоятельствах может потребоваться снижение скорости горения. Например, двигатель может иметь большое отношение L/D для создания достаточно высокой тяги, или для конкретной конструкции может быть необходимо ограничение диаметра двигателя. Следовательно, полотно будет тонким, что приведет к короткой продолжительности горения. Снижение скорости горения было бы полезно.
Например, если кто-то хочет сконструировать зерно с торцевой горелкой, которое имеет относительно небольшую площадь горения, необходимо иметь быстрогорящее топливо. В других обстоятельствах может потребоваться снижение скорости горения. Например, двигатель может иметь большое отношение L/D для создания достаточно высокой тяги, или для конкретной конструкции может быть необходимо ограничение диаметра двигателя. Следовательно, полотно будет тонким, что приведет к короткой продолжительности горения. Снижение скорости горения было бы полезно. Скорее всего, это связано с тем, что разложение ПХА является скоростьопределяющей стадией процесса горения.
Скорее всего, это связано с тем, что разложение ПХА является скоростьопределяющей стадией процесса горения. Из-за нелинейности зависимости давления от скорости горения может оказаться необходимым значительно снизить рабочее давление, чтобы получить желаемую скорость горения. Очевидным недостатком является снижение производительности двигателя, так как удельный импульс также уменьшается с уменьшением давления в камере.
Из-за нелинейности зависимости давления от скорости горения может оказаться необходимым значительно снизить рабочее давление, чтобы получить желаемую скорость горения. Очевидным недостатком является снижение производительности двигателя, так как удельный импульс также уменьшается с уменьшением давления в камере. Это идеал плотность; фактическая плотность обычно составляет 94–97% от идеальной плотности из-за крошечных пустот в зерне и зависит от технологии производства.
Это идеал плотность; фактическая плотность обычно составляет 94–97% от идеальной плотности из-за крошечных пустот в зерне и зависит от технологии производства.
 Изменение давления в камере во время стационарной фазы горения в основном связано с изменением геометрии зерен с соответствующим изменением скорости горения. Однако могут играть роль и другие факторы, такие как эрозия горловины сопла и эрозионное увеличение скорости горения.
Изменение давления в камере во время стационарной фазы горения в основном связано с изменением геометрии зерен с соответствующим изменением скорости горения. Однако могут играть роль и другие факторы, такие как эрозия горловины сопла и эрозионное увеличение скорости горения. Он поступает в виде аэрозоля в камеру тяги и контактирует со слоями катализатора.
Он поступает в виде аэрозоля в камеру тяги и контактирует со слоями катализатора.
 Третий вариант двухрежимные системы . Эти системы представляют собой гибридные конструкции, в которых гидразин используется как в качестве топлива для высокопроизводительных двухкомпонентных двигателей, так и в качестве монотоплива с обычными каталитическими двигателями малой тяги. Гидразин подается как к двухкомпонентным, так и к монотопливным двигателям из общего топливного бака.
Третий вариант двухрежимные системы . Эти системы представляют собой гибридные конструкции, в которых гидразин используется как в качестве топлива для высокопроизводительных двухкомпонентных двигателей, так и в качестве монотоплива с обычными каталитическими двигателями малой тяги. Гидразин подается как к двухкомпонентным, так и к монотопливным двигателям из общего топливного бака. В многоступенчатой ракете топливо хранится в небольших отдельных баках, а не в одном большом баке, как в одноступенчатой ракете. Поскольку каждый пустой бак выбрасывается, энергия не расходуется на ускорение пустых баков, поэтому получается более высокое общее значение V. В качестве альтернативы, большая масса полезной нагрузки может быть ускорена до того же общего V. Для удобства отдельные баки обычно комплектуются собственными двигателями, при этом каждый сбрасываемый блок называется 9.0245 этап .
В многоступенчатой ракете топливо хранится в небольших отдельных баках, а не в одном большом баке, как в одноступенчатой ракете. Поскольку каждый пустой бак выбрасывается, энергия не расходуется на ускорение пустых баков, поэтому получается более высокое общее значение V. В качестве альтернативы, большая масса полезной нагрузки может быть ускорена до того же общего V. Для удобства отдельные баки обычно комплектуются собственными двигателями, при этом каждый сбрасываемый блок называется 9.0245 этап .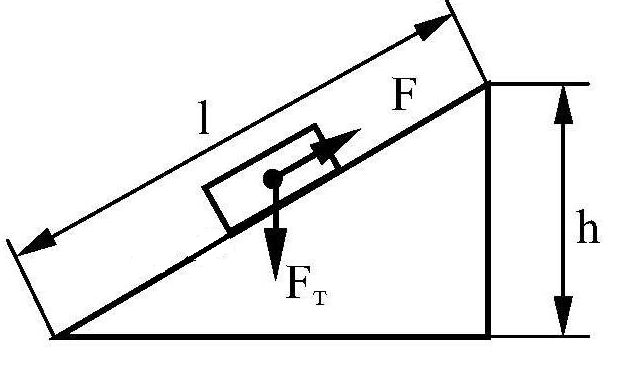 Важно понимать, что масса полезной нагрузки для любой ступени состоит из массы всех последующих ступеней плюс самой конечной полезной нагрузки. В этом случае приращение скорости для транспортного средства является суммой приращений для отдельных ступеней, где n — общее количество ступеней.
Важно понимать, что масса полезной нагрузки для любой ступени состоит из массы всех последующих ступеней плюс самой конечной полезной нагрузки. В этом случае приращение скорости для транспортного средства является суммой приращений для отдельных ступеней, где n — общее количество ступеней. После того, как выбрано распределение V, определение размеров транспортного средства выполняется, начиная с самой верхней или последней ступени (чья полезная нагрузка является фактической доставляемой полезной нагрузкой) и вычисляя начальную массу этой сборки. Затем эта сборка формирует полезную нагрузку для предыдущей ступени, и процесс повторяется до тех пор, пока не будут определены размеры всех ступеней. Результаты показывают, что для максимизации доли полезной нагрузки для данного требования V:
После того, как выбрано распределение V, определение размеров транспортного средства выполняется, начиная с самой верхней или последней ступени (чья полезная нагрузка является фактической доставляемой полезной нагрузкой) и вычисляя начальную массу этой сборки. Затем эта сборка формирует полезную нагрузку для предыдущей ступени, и процесс повторяется до тех пор, пока не будут определены размеры всех ступеней. Результаты показывают, что для максимизации доли полезной нагрузки для данного требования V: Я инженер-механик, но гидродинамика не моя сильная сторона.
Я инженер-механик, но гидродинамика не моя сильная сторона. Вместо этого имеется динамическое давление (зеленые стрелки), обратно пропорциональное скорости потока. Дисбаланс сил равен удвоенному произведению давления воздуха на площадь сопла, $F=2AP$.
Вместо этого имеется динамическое давление (зеленые стрелки), обратно пропорциональное скорости потока. Дисбаланс сил равен удвоенному произведению давления воздуха на площадь сопла, $F=2AP$.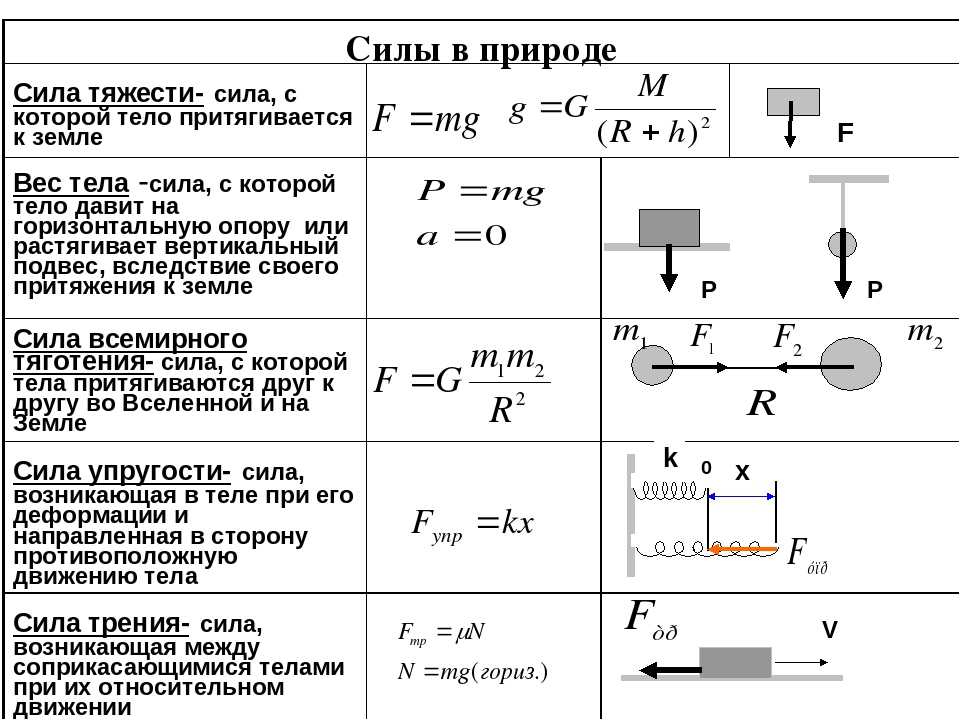 На этом этапе ваш второй метод верен: тяга — это просто площадь сопла, умноженная на давление.
На этом этапе ваш второй метод верен: тяга — это просто площадь сопла, умноженная на давление. Но, в отличие от пробок, ожидающих в стойке покоящихся относительно земли, каждая из водяных пробок движется вверх немного быстрее, чем предыдущая — достаточно быстро, чтобы соответствовать скорости ракеты. Импульс, передаваемый ракете этими движущимися заглушками, составляет дополнительную силу по сравнению со случаем, когда заглушки имеют нулевую скорость.
Но, в отличие от пробок, ожидающих в стойке покоящихся относительно земли, каждая из водяных пробок движется вверх немного быстрее, чем предыдущая — достаточно быстро, чтобы соответствовать скорости ракеты. Импульс, передаваемый ракете этими движущимися заглушками, составляет дополнительную силу по сравнению со случаем, когда заглушки имеют нулевую скорость.
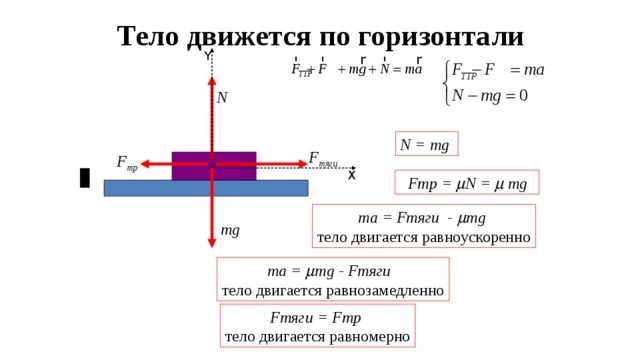 Во втором методе вы предполагаете одинаковое давление в нижней части сопла, что неверно.
Во втором методе вы предполагаете одинаковое давление в нижней части сопла, что неверно. Масса – это количество вещества в объекте, а не
под действием гравитационного притяжения Земли. Вес на руке является следствием
гравитация на массу.
Масса – это количество вещества в объекте, а не
под действием гравитационного притяжения Земли. Вес на руке является следствием
гравитация на массу.
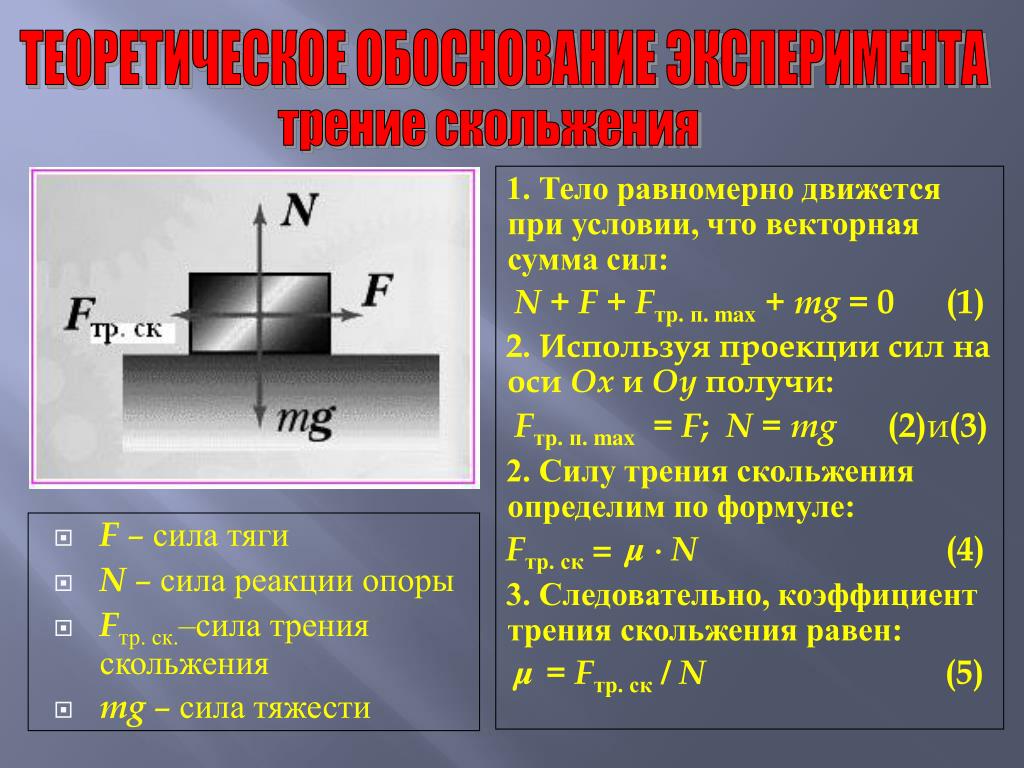


 ⓘ Массовый расход воздуха [м af ]
ⓘ Массовый расход воздуха [м af ] в минутуСантиметр в секундуКосмическая скорость — перваяКосмическая скорость — втораяКосмическая скорость — третьяСкорость ЗемлиФут в часФут в минутуФут в секундуКилометр в часКилометр в минутуКилометр в секундуУзелУзел (Великобритания)МахМах (стандарт SI)Метр в часМетр в минутуМетр в секундуМиль в часМиль в минутуМиль в секундуМиллиметр в часМиллиметр в час МинутаМиллиметр в секундуМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20°C и глубина 10 метров)Ярд в часЯрд в минутуЯрд в секунду
в минутуСантиметр в секундуКосмическая скорость — перваяКосмическая скорость — втораяКосмическая скорость — третьяСкорость ЗемлиФут в часФут в минутуФут в секундуКилометр в часКилометр в минутуКилометр в секундуУзелУзел (Великобритания)МахМах (стандарт SI)Метр в часМетр в минутуМетр в секундуМиль в часМиль в минутуМиль в секундуМиллиметр в часМиллиметр в час МинутаМиллиметр в секундуМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20°C и глубина 10 метров)Ярд в часЯрд в минутуЯрд в секунду 46 Ньютон —> Преобразование не требуется
46 Ньютон —> Преобразование не требуется
 Массовый расход воздуха — это масса всасываемого воздуха, протекающего в единицу времени. Скорость струи можно описать как движение пластины в метрах в секунду, а скорость полета определяется как положительная по направлению к хвостовой части самолета.
Массовый расход воздуха — это масса всасываемого воздуха, протекающего в единицу времени. Скорость струи можно описать как движение пластины в метрах в секунду, а скорость полета определяется как положительная по направлению к хвостовой части самолета.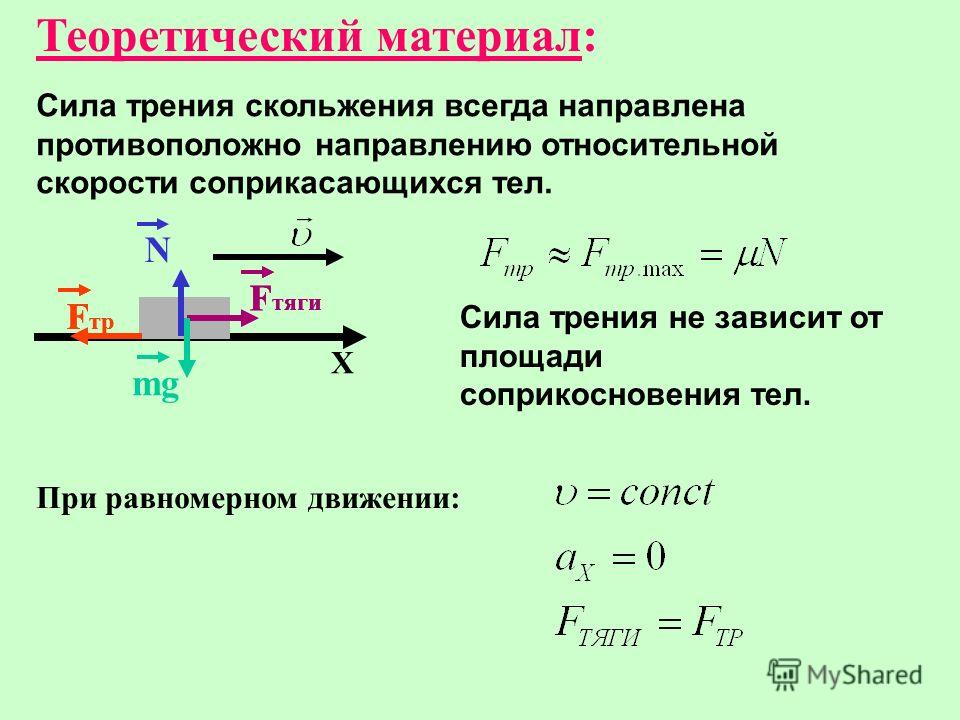 Некоторые самолеты производят тягу непосредственно от двигателей. Турбореактивные, прямоточные и ракетные самолеты являются примерами источников тяги.
Некоторые самолеты производят тягу непосредственно от двигателей. Турбореактивные, прямоточные и ракетные самолеты являются примерами источников тяги. Таким образом, разница между ними имеет значение для пилота.
Таким образом, разница между ними имеет значение для пилота.
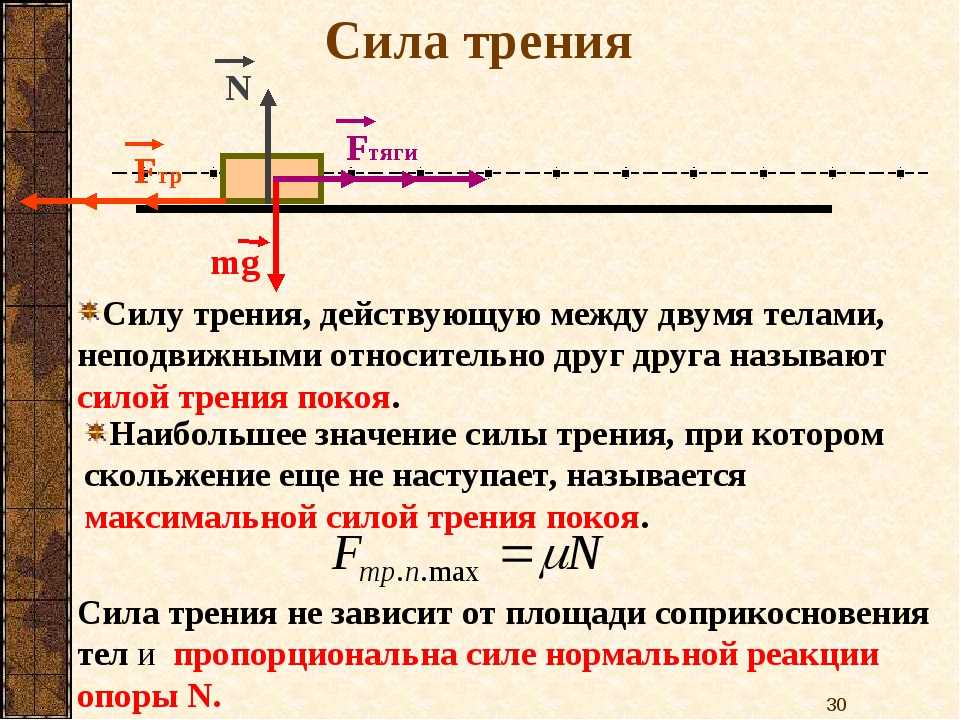 Умножение этого на скорость в футах в секунду отменяет футы и секунды, что приводит к фунтам. Другими словами, умножение массового расхода воздуха на изменение скорости этого воздушного потока дает вам тягу:
Умножение этого на скорость в футах в секунду отменяет футы и секунды, что приводит к фунтам. Другими словами, умножение массового расхода воздуха на изменение скорости этого воздушного потока дает вам тягу: 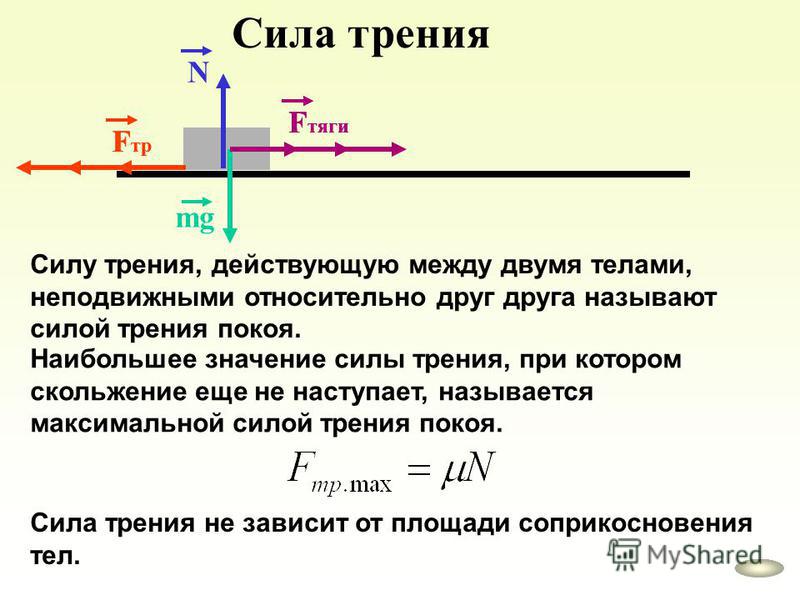
 Мы знаем, что кривая сопротивления будет равна кривой тяги, необходимой для полета без ускорения. Уравнение сопротивления, которое мы уже видели, выглядит следующим образом:
Мы знаем, что кривая сопротивления будет равна кривой тяги, необходимой для полета без ускорения. Уравнение сопротивления, которое мы уже видели, выглядит следующим образом: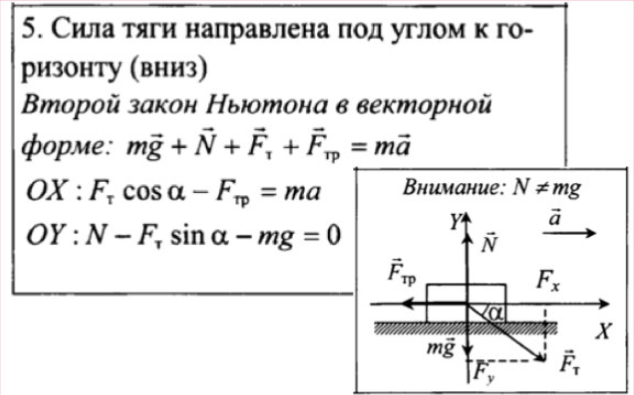 Паразитное сопротивление практически не меняется. Как мы видели на кривой сопротивления, индуктивное сопротивление больше всего на низких скоростях, в то время как паразитное сопротивление больше на высоких скоростях.
Паразитное сопротивление практически не меняется. Как мы видели на кривой сопротивления, индуктивное сопротивление больше всего на низких скоростях, в то время как паразитное сопротивление больше на высоких скоростях. Пик этой кривой известен как L/DMAX и происходит при наиболее эффективном угле атаки самолета.
Пик этой кривой известен как L/DMAX и происходит при наиболее эффективном угле атаки самолета. 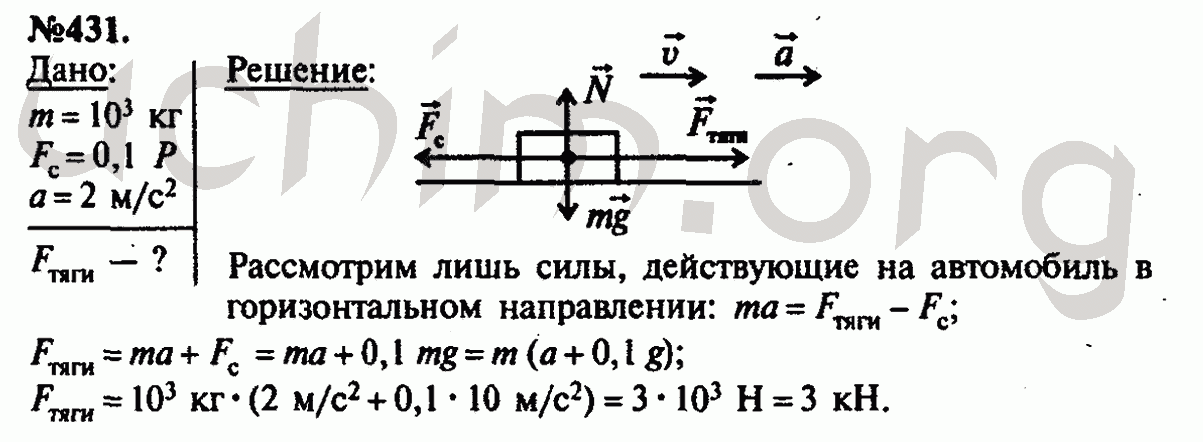
 Пересечение — это место, где достигается максимальная дальность. На примере диаграммы это точка B, около 300 узлов.
Пересечение — это место, где достигается максимальная дальность. На примере диаграммы это точка B, около 300 узлов.  Точно так же самолету, летящему с попутным ветром, помогают на его пути, и поэтому он должен снизить скорость, чтобы воспользоваться ветром ».
Точно так же самолету, летящему с попутным ветром, помогают на его пути, и поэтому он должен снизить скорость, чтобы воспользоваться ветром ».
