Формула жуковского: ПОДЪЁМНАЯ СИЛА • Большая российская энциклопедия

ПОДЪЁМНАЯ СИЛА • Большая российская энциклопедия

Авторы: Г. А. Тирский

Рис. 1. Силы, действующие на крыло: R – полная аэродинамическая сила,Y – подъёмная сила, X – сила лобового сопротивления; l – длина хорды крыла, α – угол атаки, v∞  – скорость набегающего потока.

ПОДЪЁМНАЯ СИ́ЛА, од­на из со­став­ляю­щих пол­ной аэ­ро­ди­на­мич. си­лы, дей­ст­вую­щей на те­ло, дви­жу­щее­ся в га­зе или жид­ко­сти; на­прав­ле­на пер­пен­ди­ку­ляр­но век­то­ру ско­ро­сти те­ла (рис. 1). Дей­ст­ву­ет на кры­ло и фю­зе­ляж ле­тя­ще­го са­мо­лё­та, глис­си­рую­ще­го по во­де суд­на и др. Вы­зва­на на­ло­же­ни­ем на на­бе­гаю­щий по­тен­ци­аль­ный (без­вих­ре­вой) по­ток (рис. 2, а) цир­ку­ля­ци­он­но­го по­то­ка (рис. 2, б), воз­ни­каю­ще­го во­круг об­те­кае­мо­го про­фи­ля (напр., кры­ла). Вслед­ст­вие та­ко­го на­ло­же­ния (рис. 2, в) на верх­ней сто­ро­не кры­ла ско­рость по­то­ка уве­ли­чи­ва­ет­ся, а на ниж­ней – умень­ша­ет­ся. Из Бер­нул­ли урав­не­ния сле­ду­ет, что дав­ле­ние над кры­лом умень­ша­ет­ся, а под кры­лом – уве­ли­чи­ва­ет­ся, т.  е. воз­ни­ка­ет си­ла, дей­ст­вую­щая на кры­ло сни­зу вверх, – подъ­ём­ная си­ла.

Рис. 2. Образование подъёмной силы: а – безвихревой поток; б – циркуляция вокруг крыла; в – наложение циркуляции на безвихревой поток; Y – подъёмная сила, Γ – цирку…

В 1904 Н. Е. Жу­ков­ский и позд­нее нем. ма­те­ма­тик В. Кут­та тео­ре­тически по­лу­чи­ли вы­ра­же­ние для П. с. $Y$ кры­ла, об­те­кае­мо­го по­тен­ци­аль­ным по­то­ком иде­аль­ной не­сжи­мае­мой жид­ко­сти: $Y=ρv_∞Γ$, где $ρ$ – плот­ность жид­ко­сти, $v_∞$ – ско­рость на­бе­гаю­ще­го по­то­ка, $Γ$ – ска­ляр­ная ве­ли­чи­на, опи­сы­ваю­щая цир­ку­ля­цию по­то­ка во­круг кры­ла. Эта фор­му­ла на­зы­ва­ет­ся фор­му­лой Жу­ков­ско­го или Жу­ков­ско­го – Кут­ты. При­чи­ной воз­ник­но­ве­ния цир­ку­ля­ции яв­ля­ет­ся об­ра­зо­ва­ние по­верх­но­сти раз­де­ла ме­ж­ду по­то­ка­ми, сте­каю­щи­ми с верх­ней и ниж­ней по­верх­но­стей кры­ла. Вслед­ст­вие осо­бой фор­мы кры­ла эти по­то­ки име­ют раз­ные ско­ро­сти, по­это­му по­верх­ность раз­де­ла пре­в­ра­ща­ет­ся в вихрь (цир­ку­ля­цию), ко­то­рый от­ры­ва­ет­ся и уно­сит­ся вме­сте с по­то­ком. 2_{\infty}$, где $S$ – ха­рак­тер­ная ве­ли­чи­на пло­ща­ди те­ла (напр., пло­щадь кры­ла в пла­не), $C_y$ – без­раз­мер­ный ко­эф. П. с. Эта фор­му­ла при­ме­ни­ма при об­те­ка­нии про­из­воль­ных тел как вяз­кой, так и не­вяз­кой жид­ко­стью, а так­же га­зом. Ко­эф. $C_y$ в об­щем слу­чае за­ви­сит от Рей­нольд­са чис­ла, Ма­ха чис­ла $M_∞$, уг­ла ата­ки $α$, уг­ла стре­ловид­но­сти, фор­мы кры­ла. Ко­эф. $C_y$ оп­ре­де­ля­ет­ся экс­пе­ри­мен­таль­но или чис­лен­ным ре­ше­ни­ем за­дач об­те­ка­ния. Со­глас­но тео­рии Жу­ков­ско­го, для кры­ла в плос­ко­па­рал­лель­ном по­то­ке $C_y=2m(α-α_0)$, где $α_0$ – угол ата­ки, при ко­то­ром П. с. рав­на ну­лю, $m$ – ко­эф., за­ви­ся­щий толь­ко от фор­мы про­фи­ля кры­ла (напр., для тон­кой изо­гну­той пла­сти­ны $m=π$). Учёт вяз­ко­сти жид­ко­сти умень­ша­ет мно­жи­тель $m$ и, со­от­вет­ст­вен­но, П. с. Это свя­за­но с по­яв­ле­ни­ем в вяз­кой жид­ко­сти по­гра­нич­но­го слоя, вслед­ст­вие че­го про­ис­хо­дит от­рыв по­то­ка, на про­фи­ле об­ра­зу­ет­ся об­ласть воз­врат­но­го те­че­ния с поч­ти по­сто­ян­ным дав­ле­ни­ем, что при­во­дит к умень­ше­нию П.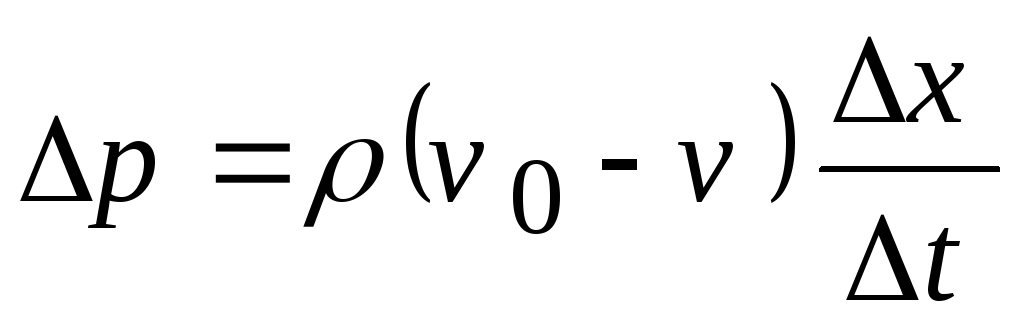  с. При уве­ли­че­нии уг­ла ата­ки за­ви­си­мость $C_y(α)$ пе­ре­ста­ёт быть ли­ней­ной. При уг­ле ата­ки, на­зы­вае­мом кри­ти­че­ским, зна­че­ние $C_y$ дос­ти­га­ет мак­си­му­ма (и умень­ша­ет­ся при даль­ней­шем рос­те $α$). Ве­ли­чи­на макс. зна­че­ния $C_y$ иг­ра­ет важ­ную роль в аэ­ро­ди­на­ми­ке: чем она боль­ше, тем мень­ше ско­рость взлё­та и по­сад­ки са­мо­лё­та. При боль­ших ско­ро­стях ста­но­вит­ся су­ще­ст­вен­ной сжи­мае­мость га­за.

При сверх­зву­ко­вых ско­ро­стях ха­рак­тер об­те­ка­ния тел су­ще­ст­вен­но ме­ня­ет­ся. Так, при об­те­ка­нии пло­ской пла­сти­ны иде­аль­ным га­зом у пе­ред­ней кром­ки свер­ху об­ра­зу­ет­ся т. н. ве­ер раз­ре­же­ния с умень­ше­ни­ем дав­ле­ния за ним, а сни­зу – удар­ная вол­на с по­вы­ше­ни­ем дав­ле­ния за ней. В ре­зуль­та­те дав­ле­ние на ниж­ней по­верх­но­сти пла­сти­ны $p_н$ ста­но­вит­ся боль­ше, чем на верх­ней $p_в$, т. е. воз­ни­ка­ет П. с. Для чи­сел Ма­ха, не­зна­чи­тель­но пре­вы­шаю­щих 1, и ма­лых $α$ ко­эф. П. с.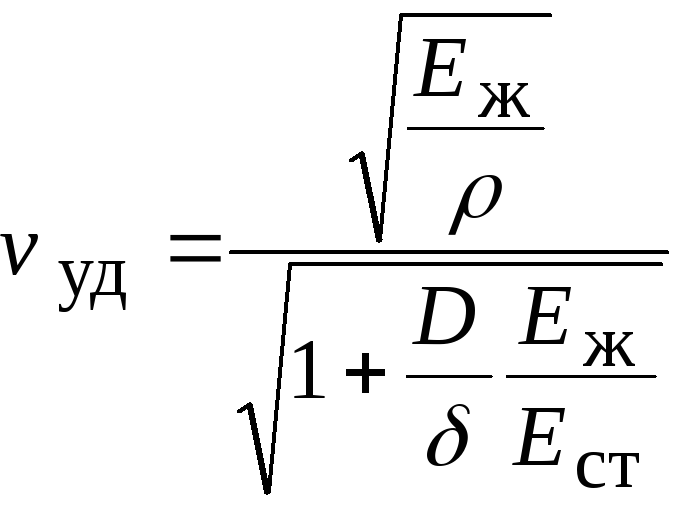 2_{\infty}-1}$. Эта фор­му­ла спра­вед­ли­ва для тон­ких про­фи­лей про­из­воль­ной фор­мы с ост­рой пе­ред­ней кром­кой. Раз­ра­бо­та­ны чис­лен­ные ме­то­ды ре­ше­ния за­дач сверх­зву­ко­во­го об­те­ка­ния тел про­из­воль­ной фор­мы как в рам­ках ре­ше­ния урав­не­ний Эй­ле­ра (иде­аль­ный газ), так и в рам­ках ре­ше­ния урав­не­ний На­вье – Сто­кса и Рей­нольд­са с учё­том фи­зи­ко-хи­мич. свойств га­за.

Важ­ной ха­рак­те­ри­сти­кой кры­ла, при­ме­няе­мой для рас­чё­та П. с., яв­ля­ет­ся т. н. по­ля­ра кры­ла – гра­фик за­ви­си­мо­сти пол­ной аэ­ро­ди­на­мич. си­лы от уг­ла ата­ки. Точ­ки на по­ля­ре да­ют зна­че­ния ко­эф. $C_y$ и ко­эф. со­про­тив­ле­ния $C_x$, от­ве­чаю­щих од­но­му и то­му же уг­лу ата­ки. От­но­ше­ние $K=C_y/C_x$ на­зы­ва­ет­ся аэ­ро­ди­на­мич. ка­че­ст­вом кры­ла. Эта ве­ли­чи­на яв­ля­ет­ся од­ной из осн. ха­рак­те­ри­стик, оп­ре­де­ляю­щих со­вер­шен­ст­во са­мо­лё­та. Так, кры­лья аль­бат­ро­са (раз­мах ко­то­рых дос­ти­га­ет 4 м, а раз­ви­вае­мая пти­цей ско­рость – 110 км/ч) име­ют ко­эф. ка­че­ст­ва 20. Эту ве­ли­чи­ну авиа­кон­ст­рук­то­рам уда­лось пре­взой­ти лишь при соз­да­нии пла­нё­ров и вы­сот­ных (во­ен­ных, спор­тив­ных) са­мо­лё­тов.

П. с. кры­ла ко­неч­но­го раз­ма­ха име­ет свои ка­че­ст­вен­ные осо­бен­но­сти: те­че­ние око­ло та­ко­го кры­ла ин­тер­пре­ти­ру­ет­ся как при­сое­ди­нён­ная вих­ре­вая нить, ко­то­рая на кон­цах кры­ла схо­дит и об­ра­зу­ет в сле­де за кры­лом два ко­неч­ных (по­гра­нич­ных) вих­ря, ко­то­рые со­еди­ня­ют­ся с на­чаль­ным вих­рем, ухо­дя­щим в бес­ко­неч­ность, об­ра­зуя под­ко­во­об­раз­ный вихрь. Эти вих­ри вы­зы­ва­ют по­яв­ле­ние ин­ду­ци­ро­ван­ной ком­по­нен­ты ско­ро­сти за кры­лом, на­прав­лен­ной вниз по по­току. Л. Прандтль ис­поль­зо­вал схе­му под­ко­во­об­раз­но­го кры­ла для рас­чё­та ин­ду­ци­ро­ван­ной П. с. с учё­том рас­пре­де­ле­ния цир­ку­ля­ций $Γ(y)$ по кры­лу ко­неч­но­го раз­ма­ха (т. н. пе­ре­мен­ная цир­ку­ля­ция). Ве­ли­чи­на $Γ(y)$ на­хо­дит­ся из ре­ше­ния осн. ин­тег­ро-диф­фе­рен­ци­аль­но­го урав­не­ния тео­рии кры­ла Пран­дт­ля и за­тем П. {L/2}Γ(y)dy$, где $L$ – раз­мах кры­ла.

Теорема жуковского о подъемной силе и направлении движения вихрей

Рассмотрим обтекание вращающегося цилиндра. Пусть цилиндр вращается в движущейся жидкости по часовой стрелке (рис. 72). На той стороне цилиндра, где скорость по окружности суммируется со скоростью по­тока, вихри образовываться не будут или их будет небольшое количество. С диамет­рально противоположной стороны образу­ется область, заполненная вихрями.

С ледовательно, процесс обтекания не будет симметричным. Рассматривая сече­ние цилиндра по нормали к оси, можно видеть, что над цилиндром скорости по­тока будут больше, чем под ним. В соот­ветствии с уравнением Бернулли; там, где скорость больше, давление меньше, и, следовательно, вверху будет пониженное дав­ление, а внизу — повышенное. В ре­зультате неравенства давлений возника­ет подъемная сила, стремящаяся двигать цилиндр в направлении, перпендикуляр­ном потоку.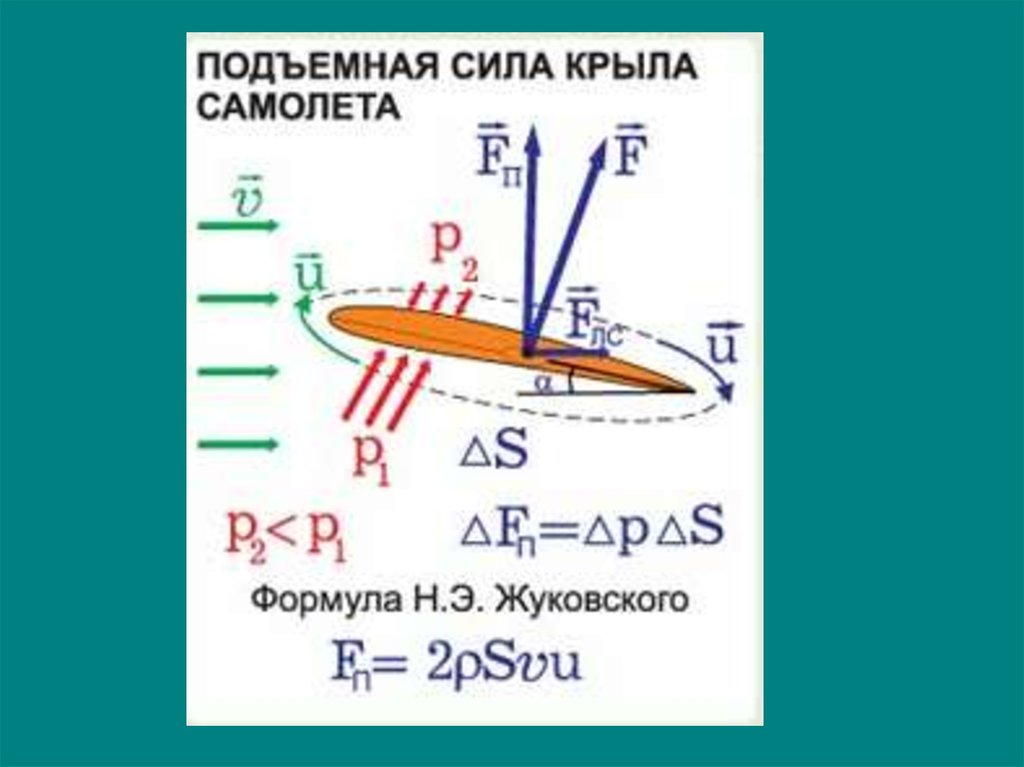

При вращении цилиндра в потоке возникают зна­чительные усилия, направленные перпендикулярно движению потока, при этом величина поперечной силы зависит от соотношения между скоростью потока и скоростью вращения цилиндра.

Подъемная сила, возникающая у вращающегося в потоке круглого цилиндра, отражает частный случай теоремы Жуковского; подъемная сила обязана своим происхождением наличию циркуляции скорости вокруг контура цилиндра.

Если через Г обозначить циркуляцию скорости, м²/сек; через v — скорость движения жидкостного потока, м/сек; через ρ – плотность жидкости, кГ∙сек²/м⁴ и через l — длину цилиндра, м, то подъемная сила R может быть выражена:

[кГ]. (11, 76)

Уравнение (II, 76) формулирует теорему Жуковского о подъемной силе: подъемная сила, возникающая вследствие циркуляции вихрей, перпендикулярная к оси потока, движущегося в бесконечности со ско­ростью

v, равна плотности жидкости, помноженной на циркуляцию, на скорость потока и на длину цилиндра.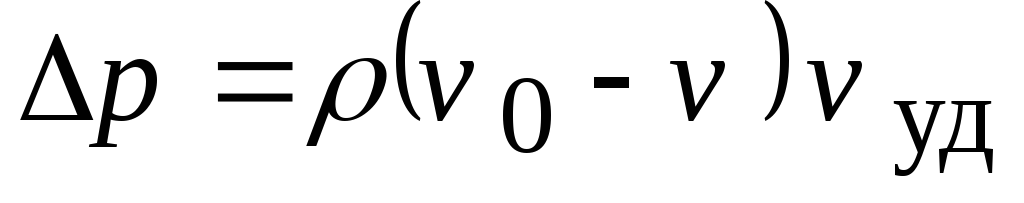

Теорема Жуковского приложима к определению подъемной силы любых тел, движущихся в жидкости. Жуковский разработал теорию присоединенных вихрей, основная идея которой заключается в том, что обтекаемые тела могут быть заменены вихрями. Поэтому можно воспользоваться теоремой Жуковского о подъемной силе применитель­но к движению самих вихрей [5]. На вихрь должна действовать та же сила, которая действовала на твердый цилиндр, т. е. сила Жуковского.

Таким образом, на любой вихрь, когда он перемещается внутри жидкости или обтекается жидкостью, всегда действует сила, направ­ленная так же, как и сила Жуковского, т. е. нормально к оси вихря и скорости обтекающего вихрь потока.

Кинетическая энергия частиц, из которых состоит вихрь, равна , где m — масса частиц; v — скорость слоя, из которого образо­вался вихрь. Часть этой кинетической энергии расходуется на кинетическую энергию вращательного движения вихря, равную , где I — момент инерции ядра вихря; ω — угловая скорость вращения ядра вихря.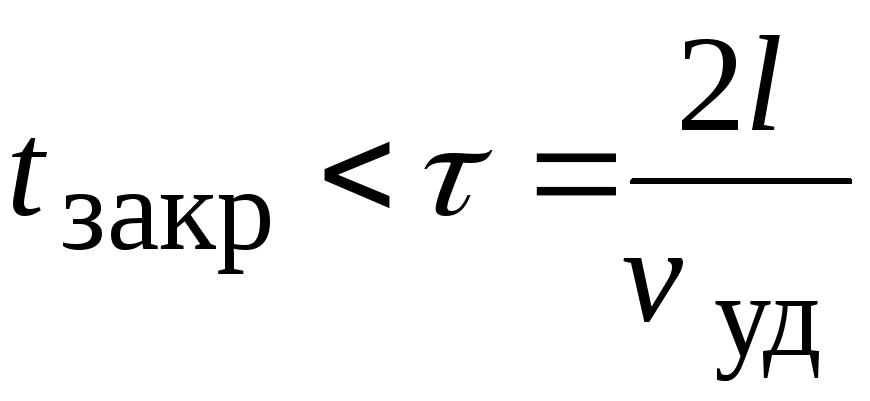 Если некоторая доля кинетической энергии вихря убав­ляется, то поступательная скорость движения вихря должна также уменьшаться. Вихрь при этом должен отставать от того слоя, из ко­торого он образовался. Перемещение вихря относительно окружаю­щей его жидкости должно создавать силу Жуковского. Последняя будет смещать вихри в направлении, где скорость больше, т. е. от пе­риферии к оси потока, и если движение происходит в трубе, то эта сила будет направлена от стенки трубы внутрь жидкости. Это положе­ние в полной мере относится к вихрям, отрывающимся от шерохова­тых стенок.

Лекция 6.

ОСНОВЫ ТЕОРИИ ПОДОБИЯ

Аналоговые методы моделирования являются основой изучения новых процессов и явлений и основаны на подобии этих явлений другим, хорошо известны.

Самым простым из этих является масштабирование, использующее геометрическое подобие. Глобус, например, моделирует Земной шар. Чем крупнее глобус (масштаб) тем точнее они моделируют землю – идеальный вариант наступит при масштабе 1:1, когда размер глобуса равен размеру Земли. Из-за большой сложности процессов обогащения полезных ископаемых их изучение, как правило, возможно только на основе моделирования. Это особенно важно при переходе от изученных лабораторных моделей к проектируемым – промышленным.

Уравнение Жуковского

Многие инженеры считают, что они могут выполнять анализ стационарного состояния в электронной таблице. Тем не менее, если они хотят посмотреть на что-то переходное, например, на скачок давления из-за внезапного закрытия клапана или из-за разрыва, симулятор просто необходим. На самом деле существует простой способ выполнить такой анализ переходных процессов вручную, который работает как для газовых, так и для жидкостных трубопроводов и во многих ситуациях является достаточно точным. Всегда полезно иметь расчет карандашом и бумагой, чтобы проверить работоспособность сложного программного обеспечения, даже если это Atmos SIM.

Уравнение Жуковского позволяет нам выполнять расчеты перенапряжений вручную. Он назван в честь Николая Жуковского, отца-основателя аэродинамики, а также гидродинамики. (В этой записи блога я буду придерживаться более распространенного написания уравнения «Жуковский»). Помимо этого уравнения, Жуковский был первым, кто физически объяснил подъемную силу на крыле самолета и получил много других важных результатов в инженерии и математике. Я не буду пытаться здесь вывести уравнение Жуковского. Тем не менее, из второго закона Ньютона следует, что сила = масса, умноженная на ускорение, в сочетании с физическим фактом, что никакое возмущение не может распространяться в жидкости быстрее, чем скорость волны (скорость волны составляет примерно 300 м/с в газопроводах и около 1 -1,5 км/с в жидкостных трубопроводах).

Уравнение Жуковского: ∆P = — ρ c ∆V. Где ∆P — величина скачка давления, вызванного изменением скорости, и это то, что мы пытаемся рассчитать: ΔV — изменение скорости, вызывающее помпаж: p — плотность жидкости, а c — скорость волны.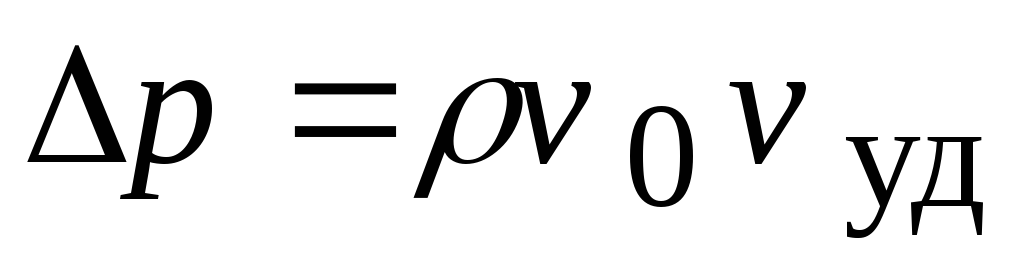 (Чтобы не было никаких коэффициентов преобразования единиц, эти величины должны быть в последовательном наборе единиц, таких как СИ: давление в паскалях, плотность в кг/м3, скорость волны и изменение скорости в м/с).

Уравнение Жуковского можно применять любым способом: можно рассчитать скачок давления, сопровождающий заданное изменение скорости: или изменение скорости, ожидаемое при внезапном изменении давления.

Например, у нас есть бензиновый трубопровод, который течет со скоростью 2 м/с, и я быстро закрываю вентиль: какой скачок давления я могу ожидать? Сверяясь со своими справочниками (или Гуглом), вижу, что плотность бензина около 800 кг/м3, а скорость звука около 1380 м/с. Бензин резко останавливается после закрытия клапана, поэтому ΔV равно -2 м/с. Тогда изменение давления на входе составляет ΔP = -1380 м/с * 800 кг/м3 * -2 м/с = 22 бар (= 320 фунтов на кв. дюйм), а на выходе -22 бар. Если клапан действительно мгновенно закроется, то скачок давления в 22 бара устремится вверх по трубе, а отрицательный скачок устремится вниз по трубе со скоростью 1380 м/с.

Это совершенно правильный результат переходной модели: мы ожидаем, что SIM даст аналогичный ответ, и это действительно так, как мы видим ниже:

Если вам нужно очень точное решение или решение, когда скачок давления прошел более 5 или 10 км, то есть несколько предостережений:

1. В конце концов, трение приведет к уменьшению высоты скачка: ширина помпажа (имеется в виду время, необходимое помпу для прохождения точки) останется такой же, как и время, необходимое для закрытия клапана. Таким образом, в нашем примере с бензином, если клапан закрылся за 1 секунду, то давление поднимется на 22 бара на высоте 1380 м, и это повышение пройдет точку в трубопроводе — даже точку, удаленную на много километров — за 1 секунду.
2. В газопроводе с достаточно большим изменением давления, при котором ΔV близко к c, что означает, что скорость газа приближается к запертому потоку, как это происходит при разрыве трубопровода, становятся важными нелинейные процессы, и результат Жуковского будет менее точным . Это связано с тем, что истинный фронт волны давления будет более рассредоточенным.
3. Чтобы этот результат был точным, вы должны использовать правильную скорость волны c. Это означает, что его необходимо настроить на расширение трубы, если вы смотрите на трубу очень большого диаметра, особенно тонкостенную трубу или пластиковую трубу (поправку для этого можно найти в Интернете или в любом инженерном справочнике. )
4. Скорость волны в системе с постоянной температурой (например, в неизолированной подводной трубе) будет отличаться от скорости волны в трубе с хорошей изоляцией.
5. В конце концов, вы начнете видеть отраженные волны от любых других закрытых клапанов в системе или чего-либо, находящегося под постоянным давлением, например, резервуара или газового резервуара.
6. В жидкой системе скачок отрицательного давления может привести к падению давления ниже уровня пара: в этом случае будет развиваться вялый поток, и динамика может стать очень сложной.

Atmos SIM автоматически справляется со всеми этими более сложными ситуациями. Но для быстрой приблизительной оценки уравнение Жуковского по-прежнему очень полезно!

См. предыдущую статью Джейсона об обработке неверных данных здесь. Вы также можете прочитать некоторые статьи Джейсона и блоги ниже:

• Блог: интервью Джейсона Модизетта
• Документ: Модель слабого потока с подвижными границами режима
• Документ: Адаптивные пространственные сетки в моделях трубопроводов
Документ
• : Оценка состояния моделей трубопроводов с использованием ансамблевого фильтра Калмана
• Статья: Неустойчивость и другие численные проблемы в конечно-разностных моделях трубопроводов

Профиль Жуковского | ЭтоМатематика

Профиль Жуковского

Опубликовано 27 февраля 2020 г.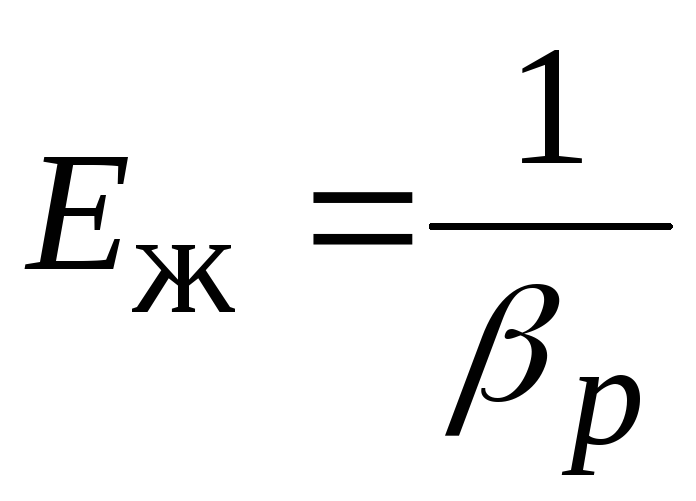 Иногда Закрыто
Теги: Прикладная математика, Гидродинамика

Простое преобразование с замечательными свойствами использовал Николай Жуковский около 19 лет.10 для изучения обтекания крыльев самолета. Он определяется как

и обычно называется Картой Жуковского . Начнем с обсуждения теории течения жидкости в двух измерениях. Читатели, знакомые с двумерным потенциальным потоком, могут сразу перейти к разделу Аэродинамический профиль Жуковского .

Визуализация воздушного потока вокруг профиля Жуковского. Изображение создано с использованием кода на этом сайте.

Аналитические функции и гармонические функции

Теория комплексных переменных является мощным инструментом моделирования течения жидкости в двух измерениях. Независимая комплексная переменная . Если функция является аналитической , то ее производная не зависит от направления приращения. Поэтому

Запись , это приводит к , что немедленно дает уравнения Коши-Римана:

Отсюда следует, что , так что ; и аналогично.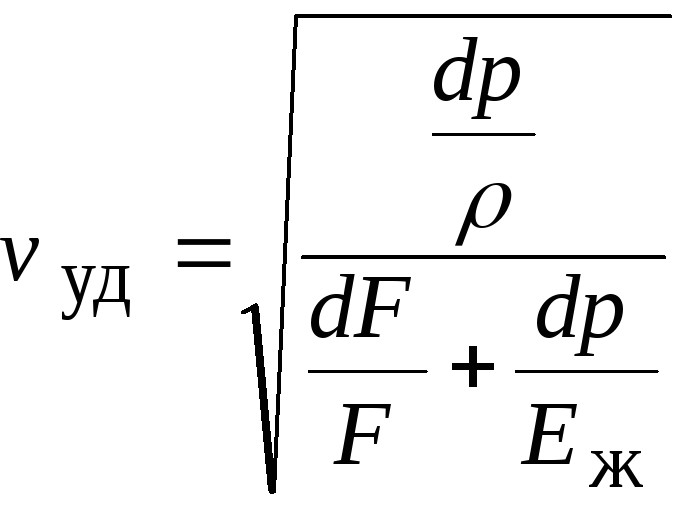 Таким образом, оба и удовлетворяют двумерному уравнению Лапласа; это гармонические функции . Это замечательно: действительная и мнимая части любой аналитической функции являются гармоническими функциями.

Комплексный потенциал

Обозначим скорость через . Для простоты рассмотрим стационарный поток жидкости (), который одновременно является безвихревым и несжимаемым: следует из этого и являются гармоническими функциями

и содержат действительную и мнимую части аналитической функции, комплексный потенциал :

Примеры потенциального потока

Пример I: 900 72 Комплексный потенциал соответствует

, что дает равномерный поток на восток

так что . Это показано на рисунке ниже (левая панель).

Потенциал скорости (синий пунктир) и функция тока (сплошной красный) для комплексных потенциалов (слева) и (справа).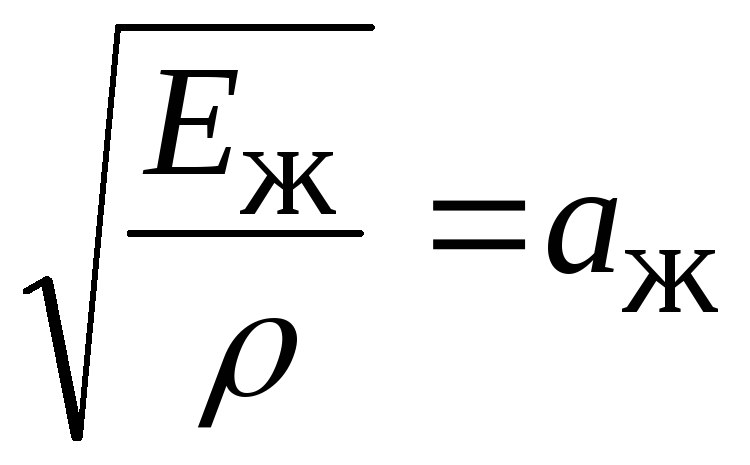

Пример II:
Потенциал имеет потенциал скорости и функцию тока

с соответствующими компонентами скорости

Это дипольный поток, показанный на рисунке выше (правая панель).

Пример III: Потенциал может быть выражен как

и соответствует потенциалу скорости и функции тока

с радиальной и тангенциальной составляющими потока

, который течет против часовой стрелки вокруг начала координат. Обратите внимание, что величина уменьшается с радиусом ровно на величину, обеспечивающую

, поэтому поток, хотя и циркулирующий, является безвихревым.

Преобразование Жуковского

Объединим комплексные потенциалы и получим потенциал с некоторыми замечательными свойствами, потенциал Жуковского

Это отображение также называют преобразованием Жуковского (Николай Жуковский изучал его около10).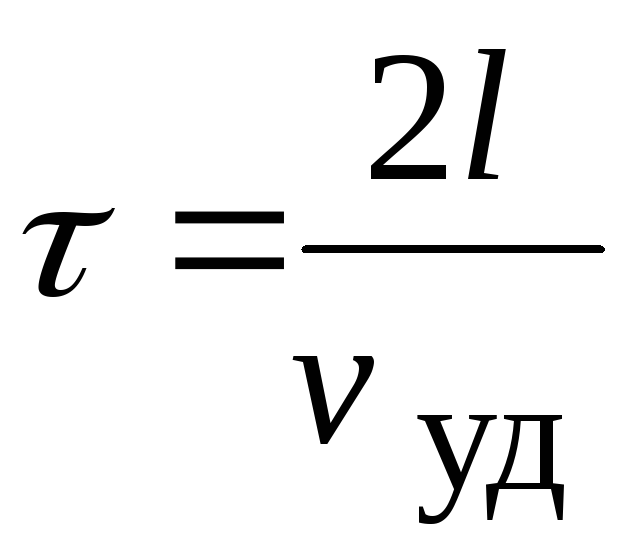 Потенциал скорости и функция тока, соответствующие

Эти функции представлены ниже. Заметим, что единичная окружность соответствует константе : поток по этой кривой отсутствует, и жидкость течет по единичной окружности или, в трех измерениях, по бесконечному цилиндру.

Потенциал скорости (синий пунктир) и функция тока (сплошной красный) для комплексного потенциала .

Из определения видно, что . Если мы ограничим отображение внешним видом единичного круга, оно будет взаимно однозначным. Переписав карту в виде , имеем два решения

Поскольку один из них находится внутри, а другой снаружи.

Пусть отображение может быть записано

Теперь, записывая, мы легко покажем, что

где и (так ). Таким образом, окружности с центром в начале координат преобразуются в эллипсы
с полуосями и . Кроме того,

, таким образом, линии, проходящие через начало координат, отображаются на гиперболы.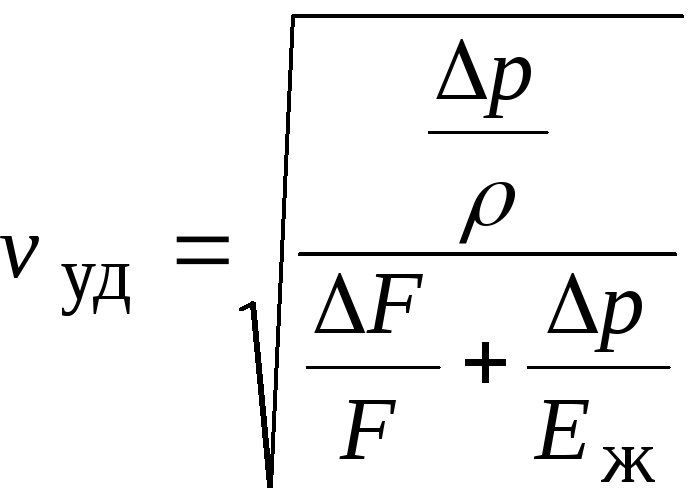

Аэродинамический профиль Жуковского

При преобразовании Жуковского единичная окружность отображается в сегмент прямой (рисунок ниже, левая панель). Когда центр круга перемещается, но все еще проходит через него, кривая изображения представляет аэродинамический профиль (правая панель).

Слева: окружность единицы измерения отображается в сегмент линии. Справа: смещенный круг превращается в кривую, представляющую аэродинамический профиль.

Отображение, которое преобразует круг в аэродинамический профиль , также отображает поток вокруг круга или, в 3D, цилиндр для обтекания аэродинамического профиля. На рисунке ниже мы показываем одну линию тока (левая панель) и соответствующую линию тока вокруг аэродинамического профиля (правая панель).

Слева: обтекаемая линия вокруг цилиндра. Справа: соответствующая линия обтекания аэродинамического профиля.

Добавление циркуляции

В приведенном выше примере III мы видели, что потенциал подразумевает циркуляцию вокруг крыла.