Подъемная сила это: Подъёмная сила — это… Что такое Подъёмная сила?

Подъёмная сила — это… Что такое Подъёмная сила?

Четыре силы, действующие на самолёт

Подъёмная сила — составляющая полной аэродинамической силы, перпендикулярная вектору скорости движения тела в потоке жидкости или газа, возникающая в результате несимметричности обтекания тела потоком. В соответствии с законом Бернулли, статическое давление среды в тех областях, где скорость потока более высока, будет ниже, и наоборот. Например, крыло самолета имеет несимметричный профиль (верхняя часть крыла более выпуклая), вследствие чего скорость потока по верхней кромке крыла будет выше, чем над нижней. Создавшаяся разница давлений и порождает подъёмную силу. Полная аэродинамическая сила — это интеграл от давления вокруг контура крыла.

где:

• Y — это подъёмная сила,
• P — это тяга,
•  — граница профиля,
• p — величина давления,
• n — нормаль к профилю

Согласно теореме Жуковского, величина подъёмной силы пропорциональна плотности среды, скорости потока и циркуляции скорости потока.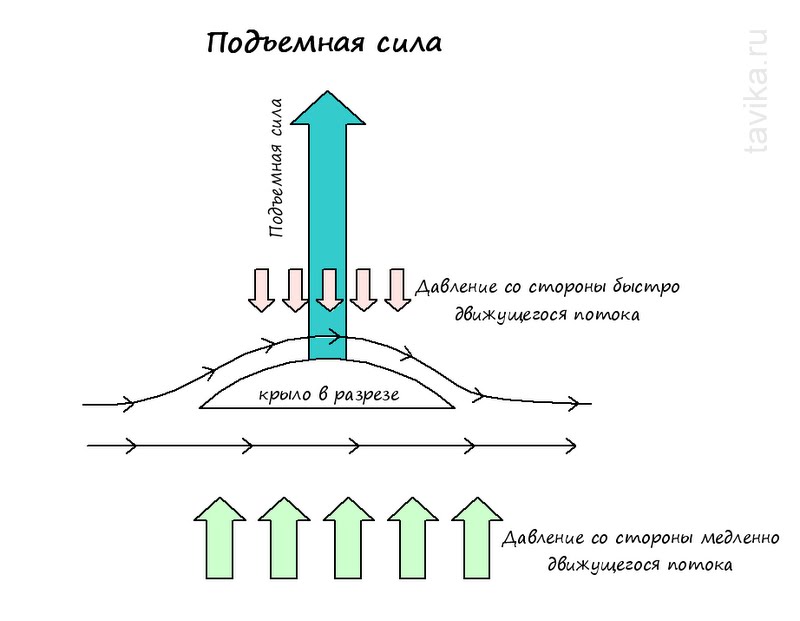

Коэффициент подъёмной силы

Коэффициент подъёмной силы — безразмерная величина, характеризующая подъемную силу крыла определённого профиля при известном угле атаки. Коэффициент определяется экспериментальным путём в аэродинамической трубе, либо по теореме Жуковского. Формулу расчёта подъёмной силы через коэффициент разработали братья Райт и Джон Смитон в начале XX века^{[уточнить]} . Формула имеет вид^[1]:

где:

 — подъёмная сила (Н)

 — коэффициент подъёмной силы

 — весовая плотность воздуха на высоте полёта (кг/м³)

 — скорость набегающего потока (м/с)

 — характерная площадь (м²)

При расчетах по этой формуле важно не путать весовую и массовую плотность воздуха. Весовая плотность при стандартных атмосферных условиях (на уровне земли при температуре +15 С) равна =1. 225 кг/м³. Но в аэродинамических расчетах часто используют массовую плотность воздуха, которая равна 0.125 кг*с²/м⁴. В этом случае подъемная сила Y получается не в ньютонах (Н), а в килограммах (кг). В книгах по аэродинамике не всегда имеются уточнения, о какой плотности и размерности подъемной силы идет речь, поэтому в спорных ситуациях нужно проверять формулы, сокращая единицы измерения.

Примечания

1. ↑ Clancy, L.J., Aerodynamics, Section 4.15

Ссылки

Подъемная сила крыла самолета: формула

Прежде чем рассматривать, что же такое подъемная сила крыла самолета и как ее рассчитать, мы представим, что авиалайнер – это материальная точка, которая осуществляет движение по определенной траектории. Для смены этого направления либо силы движения необходимо ускорение. Оно бывает двух видов: нормальное и тангенциальное. Первое стремится поменять направление движения, а второе оказывает влияние на скорость движения точки.

Если говорить о самолете, то его ускорение создается за счет подъемной силы крана. Рассмотрим конкретнее это понятие.

Подъемная сила входит в состав аэродинамической силы. Она резко возрастает, когда меняется угол атаки. Таким образом, маневренность воздушного судна заложена непосредственно в подъемной силе.

Подъемная сила крыла самолета: формула

Расчет подъемной силы крыла самолета выполняется при помощи специальной формулы: Y= 0.5 ∙ Cy ∙ p ∙ V ∙ 2∙ S.

1. Cy – это коэффициент подъемной силы крыла самолета.
2. S – площадь крыла.
3. Р – плотность воздуха.
4. V – скорость потока.

Аэродинамика крыла самолета, которая оказывает влияние на него при полете, вычисляется таким выражением:

F= c ∙ q ∙ S, где:

• C – это коэффициент формы;
• S – площадь;
• q – скоростной напор.

Следует отметить, что кроме крыла, подъемная сила создается при помощи других составляющих, а именно хвостового горизонтального оперения.

Те, кто интересуются авиацией, в частности ее историей, знают, что впервые самолет взлетел в 1903 году. Многих интересует вопрос: почему это случилось так поздно? По каким причинам это не случилось раньше? Все дело в том, что ученые на протяжении долгого времени недоумевали, каким образом высчитать подъемную силу и определить размер и форму крыла воздушного судна.

Если брать закон Ньютона, то подъемная сила пропорциональна углу атаки во второй степени. Из-за этого многие ученые считали, что невозможно изобрести крыло самолета малого размаха, но при этом с хорошими характеристиками. Лишь в конце IXX века братья Райт решили создать конструкцию небольшого размаха с нормальной силой подъема.

Центровка самолета

Что влияет на поднятие самолета в воздух?

Очень многие люди боятся летать на самолетах, потому что не знают, как он летает, от чего зависит его скорость, на какую высоту он поднимается и многое другое. Изучив это, некоторые меняют свое мнение. Каким же образом самолет поднимается вверх? Давайте разбираться.

Присмотревшись к крылу воздушного судна, можно увидеть, что оно не плоское. Нижняя часть гладкая, а верхняя – выпуклая. Благодаря этому, когда увеличивается скорость самолета, изменяется давление воздуха на его крыло. Так как внизу скорость потока небольшая, давление увеличивается. А поскольку вверху скорость увеличивается, давление уменьшается. За счет таких изменений самолет тянется вверх. Такая разница носит название подъемная сила крыла самолета. Этот принцип сформулировал Николай Жуковский в начале 20 века. При начальных попытках отправить судно в воздух применялся данный принцип Жуковского. Нынешние судна осуществляют полет со скоростью 180—250 км/ч.

Скорость лайнера при взлете

Когда лайнер набирает скорость, он непосредственно поднимается вверх. Скорость отрыва бывает разной, она зависит от габаритов самолета. Еще немаловажное влияние оказывает конфигурация его крыльев. Например, знаменитый ТУ-154 летает со скоростью 215 км/ч, а Boeing 747—270 км/ч. Чуть меньше скорость полета у Airbus A 380—267 км/ч.

Если брать средние данные, то сегодняшние лайнеры осуществляют полет со скоростью 230-240 км/ч. Однако скорость может меняться из-за ускорения ветра, массы лайнера, погоды, взлетной полосы и других факторов.

Скорость при посадке

Следует отметить, что посадочная скорость тоже непостоянна, как и взлетная. Она может меняться в зависимости от того, какая модель авиалайнера, какая площадь его, направление ветра и т. п. Но если брать средние данные, то самолет приземляется со средней скоростью 220—240 км/ч. Примечательно, что скорость в воздухе вычисляется относительно воздуха, а не земли.

Высота полета самолета

Многих интересует вопрос: какая высота полета авиалайнеров? Надо сказать, что и в этом случае конкретных данных нет. Высота может быть разной. Если же брать средние показатели, то пассажирские лайнеры летают на высоте 5—10 тыс. метров. Крупные пассажирские самолеты летают с большей высотой — 9—13 тыс.

метров. Если самолет набирает высоту выше 12 тыс. метров, то он начинает проваливаться. Из-за того, что воздух разреженный, отсутствует нормальная сила подъема и имеется недостаток кислорода. Именно поэтому не стоит взлетать так высоко, поскольку есть угроза авиакатастрофы. Зачастую самолеты выше 9 тыс. метров не поднимаются. Примечательно, что и чересчур низкая высота негативно сказывается на полете. Например, ниже 5 тыс. метров нельзя летать, так как есть угроза недостатка кислорода, в результате чего снижается мощность двигателей.

Что может стать причиной отмены полета самолета?

Принято считать, что отмена того или иного рейса происходит только из-за неблагоприятной погоды либо неполадок в самом летательном устройстве. Это вовсе не так, отмена рейса может произойти по таким причинам:

• низкая видимость, когда нет никакой гарантии, что пилот сможет посадить самолет в нужном месте. В таком случае лайнер может просто не увидеть взлетно-посадочную полосу, из-за чего может возникнуть авария;
• техническое состояние аэропорта. Бывает, что какие-то оборудования в аэропорту перестали работать или случились неполадки в работе той или иной системы, из-за чего рейс может быть перенесен на другое время;
• состояние самого пилота. Неоднократно случалось такое, что пилот не мог управлять рейсом в нужный момент и появлялась надобность в замене. Ни для кого не секрет, что в лайнере всегда два пилота. Именно поэтому необходимо определенное время, чтобы найти второго пилота. Таким образом, рейс может немного задержаться.

Лишь при полной подготовке и при благоприятных метеорологических условиях можно отправлять воздушное судно в полет. Решение об отправке принимает командир самолета. Он несет полную ответственность за то, чтобы самолет благополучно осуществил авиарейс.

Facebook

Twitter

Вконтакте

Одноклассники

Google+

Подъемная сила — Энциклопедия по машиностроению XXL

Из-за вязкого трения течение жидкости около поверхности затормаживается, поэтому, несмотря на то что наибольший прогрев жидкости, а соответственно и подъемная сила при естественной конвекции будут около теплоотдающей поверхности, скорость движения частиц жидкости, прилипших к самой поверхности, равна нулю (см. рис. 9.1).  [c.78]

К сожалению, пределы изменения расходной концентрации ц в (Л. 275] не указаны. Так как критическая скорость определяет динамическое равновесие между максимальной подъемной силой и весом материала, то Укр соответствует понятию о взвешивающей скорости массы частиц применительно к горизонтальному транспорту. Киносъемка в Л. 115], данные [Л. 275] и др. показывают, что при распределение частиц по поперечному сечению сравни-  

[c.61]

Жесткие МД изготавливаются из алюминиевого сплава. На поверхность дисков наносится магнитное покрытие. Для увеличения скорости передачи данных требуется увеличивать скорость движения носителя. В современных НМД частота вращения дисков может быть до 3600 об/мин. Во избежание интенсивного износа магнитных головок и носителя используется бесконтактный способ записи с плавающими головками. При этом между магнитными головками и поверхностью носителя создается зазор в 3. ..5 мкм за счет подъемной силы, действующей на специальный башмак, удерживающий головки.  [c.41]

Моменты от дополнительных подъемных сил АР и от веса залитой воды ДО, возникающие вследствие наклона сосуда, одинаковы ПО величине, но противоположны по направлению и поэтому не влияют  [c.71]

Зная закон распределения давлений, можно вычислить подъемную силу на башмаке и координату центра давления.  [c.201]

Воздушный шар, вес которого равен О, удерживается в равновесии тросом ВС. На шар действуют подъемная сила О и горизонтальная сила давления ветра, равная Р. Определить натяжение троса в точке В и угол а.  [c.17]

Спортивный самолет массы 2000 кг летит горизонтально с ускорением 5 м/с , имея в данный момент скорость 200 м/с. Сопротивление воздуха пропорционально квадрату скорости и при скорости в 1 м/с равно 0,5 Н. Считая силу сопротивления направленной в сторону, обратную скорости, определить силу тяги винта, если она составляет угол в 10° с направлением полета. Определить также величину подъемной силы в данный момент.  [c.199]

Ответ Сила тяги равна 30 463 Н, подъемная сила равна 14 310 Н.  [c.199]

Самолет массы 10 кг приземляется на горизонтальное поле на лыжах. Летчик подводит самолет к поверхности без вертикальной скорости и вертикального ускорения в момент приземления. Сила лобового сопротивления пропорциональна квадрату скорости и равна 10 Н при скорости в 1 м/с. Подъемная сила пропорциональна квадрату скорости и равна 30 Н при скорости в 1 м/с. Определить длину и время пробега самолета до остановки, приняв коэффициент трения / = 0,1.  [c.204]

Аэростат весом Q поднимается вертикально и увлекает за собой сложенный на земле канат. На аэростат действует подъемная сила Р, сила тяжести и сила сопротивления, пропорциональная квадрату скорости R = — х . Вес единицы длины каната у. Составить уравнение движения аэростата.  [c.338]

Определить подъемную силу воздушного шара, наполненного водородом, если объем его на поверхности земли равен 1 м при давлении р = 100 кПа и температуре  [c. 25]

На поверхности земли подъемная сила воздушного шара, наполненного водородом, равна разности сил тяжести (весов) воздуха и водорода в объеме шара  [c.25]

Следовательно, подъемная сила шара  [c.26]

Определить необходимый объем аэростата, наполненного водородом, если подъемная сила, которую он должен иметь на максимальной высоте Н = 7000 м, равна 39 240 Н. Параметры воздуха на указанной высоте принять равными р = 41 кПа, / = —30° С.  [c.26]

Насколько уменьшится подъемная сила аэростата при заполнении его гелием Чему равен объем аэростата на поверхности земли при давлении р = 98,1 кПа и температуре I = 30° С  [c.26]

При использовании этих представлений д.ля расчета силы, действующей на вращающуюся сферическую частицу, получено следующее выражение для подъемной силы [655]  [c.41]

Приведенные соотношения показывают, что отношение подъемной силы к силе сопротивления, определенных по уравнениям (2. 20) II (2.2), равно  [c.42]

При рассмотрении массоотдачи от пузырька, поднимающегося вверх, к окружающей жидкости делается ряд допущений и упрощений. Так, считается, что в относительно неглубоком резервуаре жидкости объем пузырька постоянен, поскольку тепло- и массо-отдача от пузырька, с одной стороны, и изменение давления гидростатического столба — с другой, действуют противоположным образом и сами по себе незначительны. Скорость всплывания II эффективную толщину пленки также можно считать неизменными. Предполагается далее, что пузырек всплывает под действием собственной подъемной силы и что в непосредственной близости к пузырьку состав жидкости постоянен во всех точках. С учетом этих предположений уравнение переноса массы от пузырька к жидкости имеет следующий вид [1281  [c.127]

Уравнения (9.1) и (9.2) отражают тот факт, что по мере оседания твердых частиц конечного объема жидкость вытесняется вверх. Уравнение (9.3) описывает силы, действующие на твердые частицы подъемную силу, силу сопротивления жидкости и градиент давления. Уравнение (9.4) выражает общее количество движения системы. Из уравнений (9.1), (9.2) и (9.5) следует  [c.387]

Решение. На падающий шар действуют сила тяжести Р и подъемная сила Т (рис. 211, а). Составляя уравнение (2) в проекции на вертикаль, найдем, что  [c.188]

Когда будет сброшен балласт (рис. 211, б), вес шара станет равен Р—Q, а подъемная сила останется той же. Тогда, учитывая что шар при этом движется вверх, получим  [c.188]

При малых токах (меньше 30 А) это движение вызывается подъемными силами, возникаюш,ими из-за того, что плотность горячей плазмы меньше плотности окружающей атмосферы. Дуги, в которых характер движения газа определяется свободной конвекцией, относятся к слаботочным дугам. В этой связи интересно отметить, что само название дуга произошло от той формы, которую принимает газовый разряд низкой интенсивности между горизонтальными электродами под влиянием подъемных сил.  [c.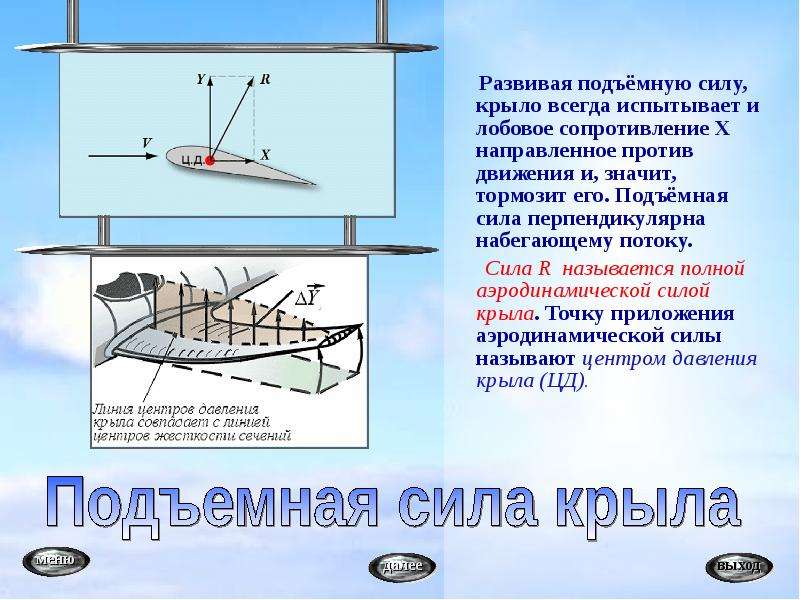 76]

Здесь через х обозначена величина волнового сопротивления (2.1), через Ф — равный нулю расход газа сквозь контур аЬ, через С подъемная сила плоского профиля, равная интегралу по контуру аЬ  [c.67]

Подъемная сила тела вращения при осесимметричном течении равна нулю. Поэтому равенство (2.8) записано в такой форме, что оно имеет смысл только для плоских течений, а в осесимметричном случае превращается в тождество.  [c.67]

Пусть необходимо найти форму контура, имеющего минимальное волновое сопротивление х заданных концевых точках а и Ь, при заданной подъемной силе ( и определенной характеристике ос набегающего потока газа. Существенно, что все необходимые величины, а также условия задачи теперь выражены через функции на характеристиках ас и Ьс. Величина х> например, при заданных функциях А(У), 0(У), [c.68]

В связи с вариационными задачами 1 и 2 следует заметить, что величина подъемной силы С не может задаваться совершенно произвольно, а должна быть заключена в некоторых пределах. Это следует из того, что интегралы, входящие в выражение (2.8), ограничены при конечных пределах.  [c.70]

Величины Аз и А4 являются постоянными, а Аг(у) и Х у) — переменными множителями Лагранжа. При постановке частных вариационных задач некоторые из условий задачи 1 могут не использоваться. Например, в задаче о плоском профиле может не задаваться подъемная сила (. В этом случае в сумме (2.20) достаточно положить равным нулю соответствующий множитель Лагранжа.  [c.71]

Полученное решение представляет, с одной стороны, осесимметричное течение, в котором подъемная сила ( обязательно равна нулю, с другой стороны — плоское течение, в котором подъемная сила может быть задана. Таким образом, здесь нельзя говорить о самой общей вариационной задаче. В связи с этим рассмотрим различные конкретные случаи. Порядок расчета при Лз(1 — i/) = 0. Этот случай представляет либо плоское течение, в котором величина подъемной силы не задается, либо осесимметричное течение.  [c.80]

При Аз(1 — Z/) = о из (2.36) следует, что A4 > 0, если на всей экстремали д Ф Q, а Ф тг/2. При этих условиях величина «9 не меняет знак на экстремали. Если t = 0 в одной точке, то = 0 на всей экстремали. Этот случай имеет место, например, тогда, когда величина X не задается. При решении такой задачи необходимо положить величину A4 равной нулю. Тогда из (2.40) находим, что = 0 на экстремали. Это приводит к важному частному выводу в плоской задаче без ограничения на подъемную силу ( и длину X проекции искомого контура на ось х, а также в осесимметричном случае без ограничения на X угол наклона скорости к оси X на экстремали равен нулю.  [c.84]

Пусть, далее, искомый контур должен обеспечивать минимальное сопротивление х- В плоском случае можно дополнительно потребовать, чтобы профиль аЬ давал заданную подъемную силу  [c.148]

В важном частном случае г(1 — и) — О (осесимметричные течения или плоские течения без ограничения подъемной силы профиля) из (6. 24), (6.25) вытекает неравенство Ug дополнительных условиях ii О, (т > 0. Равенство (6.21) показывает, что в этом случае увеличение ст уменьшает величину J°, которая при выполнении изопериметрических условий и дифференциальных связей задачи 6 отличается от х на постоянную величину. Иными словами, сопротивление любого контура может быть уменьшено, если U О допустима.  [c.153]

Рж (архимедовой силы А= —p g и силы тяжести G = pg  [c.78]

Подъемная сила Fn перемещает прогретую жидкость вверх без каких-либо побуждающих устройств (возникает естественная конвекция). Все рассуждения о возникновении естественной конвекции справедливы и для случая о хлаж-дения жидкости с той лишь разницей, что жидкость около холодной поверхности будет двигаться вниз, поскольку ее плотность будет больше, чем вдали от поверхности.  [c.78]

Оно xapaKTepHjyei отношение подъемной силы, возникающей вследствие теплового расширения жидкости, к силам вязкости.  [c.83]

При неодинаковой температуре в сечении возникает естественная конвекция и создается подъемная сила. Это влияет па п[)офиль скорости, причем характер изменения профиля скорости зависит от того как расположена труба, вертикально или горизонтально, и совпадают ли направления свободного и вынужденного движений или они противоположны. Для вертикальной трубы в случае совпадения направлений свободного и вынужденного течений (при охлаждении капельной жидкости и подаче ее сверху или нагреве жидкости и подаче ее снизу) у стенки трубы скорость возрастает, а в центре уменьшается (рис. 1.7, а). В случае противоположно направленных свободного и вынужденного течений (при охлаждении капельной жидкости и подаче ее снизу или нагревании жидкости и подаче ее сверху) скорость у стенки трубы становится меньше, а в центре больше (рис. 1.7, 6).  [c.21]

Свободный, или естественный, теплообмен возникает в неравномерно нагретом газе или жидкости, находяш,ихся как в ограниченном, так и в неограниченном пространстве. Если тело имеет более высокую температуру, чем окружаюш,ая его жидкость, то слои жидкости, нагреваясь от тела, становятся легче и под действием возникаюш,ей подъемной силы поднимаются вверх, а на их место поступают из окружающего пространства более холодные слри. Поэтому и возникает естественная конвекция.  [c.440]

При больших числах Рейнольдса частицы смещение точки отрыва вследствие вращения вызывает силу, действующую в противоположном направлении [349]. Эта сила возникает при вращении малой частицы, когда ее диаметр меньше характерного размера турбу.тентных вихрей, или в непосредственной близости от стенки толщины вязкого подслоя [742]. Влияние градиента скорости на сферу было рассчитано в работе [902], а на цилиндр — в работах [489, 832]. Сэфмен [675] вычислил подъемную силу действующую на сферу со стороны вязкой жидкости при малой скорости и в простейшем случае, когда поперечный сдвиг ) (произ-  [c.41]

Подъемной силой, действующей на мелкие частицы, находящиеся в области течения с поперечным сдвигом, можно пренебречь, если характерные числа Рейно. льдса или (dl /iZг/)/v малы.  [c.43]

При рассмотрении поднимающегося газового пузырька в гравита-ционно.м поле с ускорением д, когда подъемная сила уравнивается сопротивлением [481], влияние турбулентности потока выражается зависимостью  [c.111]

Вязкость, обусловленная поперечным сдвигом, и объемная (вторая) вязкость. Роль сопротивления, подъемной силы и врахцающего момента, действующих на частицу в вязком слое, рассматрива.лась в разд. 2.3, Кроме того, этой проблеме посвящена работа [182]. Напряжение сдвига в облаке частиц, обусловленное градиентом скорости, можно приближенно выразить следующим образом  [c.220]

Чтобы иметь представление о порядке величин различных параметров, расс.мотрим случай взаимодействия между твердыми частицалш и стенкой при движении частиц в турбулентном поле, когда диаметр частиц мал, например менее 1 мк, отношение масс газа и твердой фазы достигает 3, а отношение плотностей равно, например, 2000. Как указано выше, коэффициент трения на стенке вследствие удара твердых частиц составляет величину порядка 0,1, а напряжение сдвига — порядка 0,5-10 кг/см , для газа с коэффициентом трения 0,001 напряжение сдвига равно 0,5-10″ кз/сэ4 . Однако, как можно видеть по результатам измерений для трубы (разд. 4.1), интенсивность действительных столкновений со стенкой на порядок меньше вычисленной величины из-за подъемной силы, действующей на частицы в вязком слое [уравнение (2.23)1.  [c.236]

Влияние колебаний на движение мелких пузырей газа в жидкости изучалось в работе [57]. В зависимости от величины ускорения и частоты колебаний пузырь может погрузиться, вместо того чтобы всп.лыть под действием подъемной силы. Розенберг [653] изучал движение очень ме.лких пузырей в ультразвуковом поле. В работе [406] исс.ледовался процесс сх.лопывания пузырей.  [c.264]

Другими слова ш, несмотря на большую величину сдвига у передней кромки, для придания частице вращательного движения, которое обусловило бы значительную подъемную силу, требуется определенное время.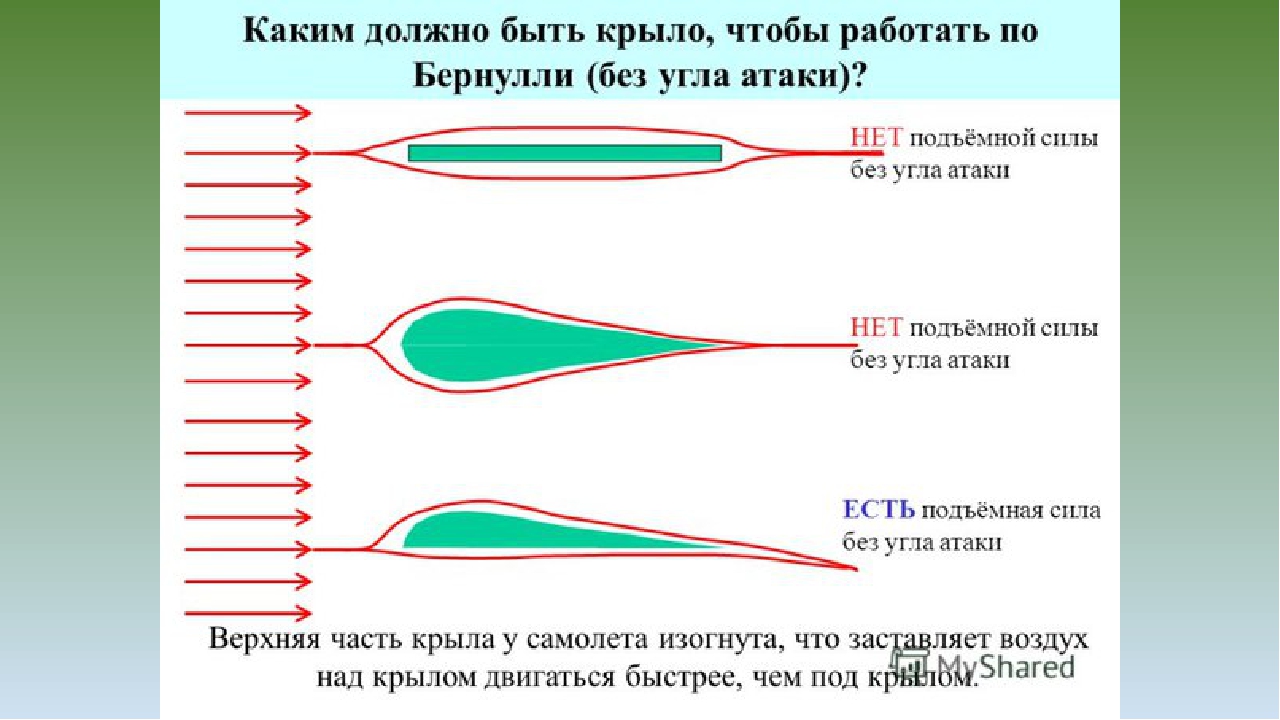 Поэтому при малых значениях а подъем частицы, обусловленный течением со сдвигом, незначителен по сравнению с подъемом, вызываемым поперечной составляющей скорости жидкости. В предельном случае при х — и1Р рассматриваемое выше отношешю принимает значение  [c.354]

Видно, что, хотя подъемная сила, вызываемая течением со сдвигом, вблизи передней кромкп обычно мала, ее влияние в области вниз по потоку мон ет быть довольно значительным. Это определяет необходимую степень уточнения полученных характеристик пограничного слоя.  [c.354]

Вьщелим в поле течения, определяемого изломом контура (рис. 3.22) кривую as, на которой а и связаны равенством (4.8) при п = 0. В задаче без ограничений на подъемную силу величина A3 = 0. Если же значение ( задано, то величина Л3, может быть определена только в результате рещения всей задачи. Предполагается, что области as соответствует часть области (4.11), а области, расположенной вниз по течению от линии as, — часть области (4. 12). Для точек h, расположенных в области as или ее части, могут быть найдены концевые точки контура Ь, которые можно считать заданными при постановке задачи.  [c.118]

---

Циркуляция н подъемная сила — Энциклопедия по машиностроению XXL

Циркуляция н подъемная сила 31, 62 Число Рейнольдса 79 Шаг 143, 155  [c.162]

Теорема Н. Е. Жуковского о подъемной силе связывает подъемную силу крыла с величиной циркуляции скорости. Согласно этой теореме подъемная сила равна произведению скорости движения летательного аппарата, плотности воздуха и величине циркуляции скоростей. Подъемная сила составляет прямой угол с направлением скорости полета.  [c.52]

Устанавливаемая формулой (38,4) связь подъемной силы с циркуляцией скорости составляет содержание теоремы Н. Е. Жуковского (1906). К применению этой теоремы к хорошо обтекаемым крыльям мы вернемся еще в 46.  [c.220]

Н. Е. Жуковский доказал основную теорему о подъемной силе крыла, сформулировал гипотезу для подсчета циркуляции скорости около профиля крыла с острой задней кромкой, предложил ряд теоретических профилей крыльев и разработал вихревую теорию гребного винта. Все это сделало его творцом новой науки —аэромеханики, являющейся теоретической основой авиационной техники.  [c.18]

Н. Е. Жуковский доказал, что источником подъемной силы крыла является циркуляционное движение жидкости вокруг его профиля (см. рис. 8.5, а), и установил зависимость между подъемной силой Яу и циркуляцией скорости  [c.127]

Поскольку обтекание пластины циркуляционное, согласно теореме Жуковского на ней возникает поперечная сила, равная р ыо Г. Величина циркуляции Г здесь не определена и в рассматриваемой теоретической схеме может быть выбрана произвольно. Однако очевидно, что только одно значение циркуляции может дать истинное значение силы Жуковского, совпадающее с полученным экспериментально.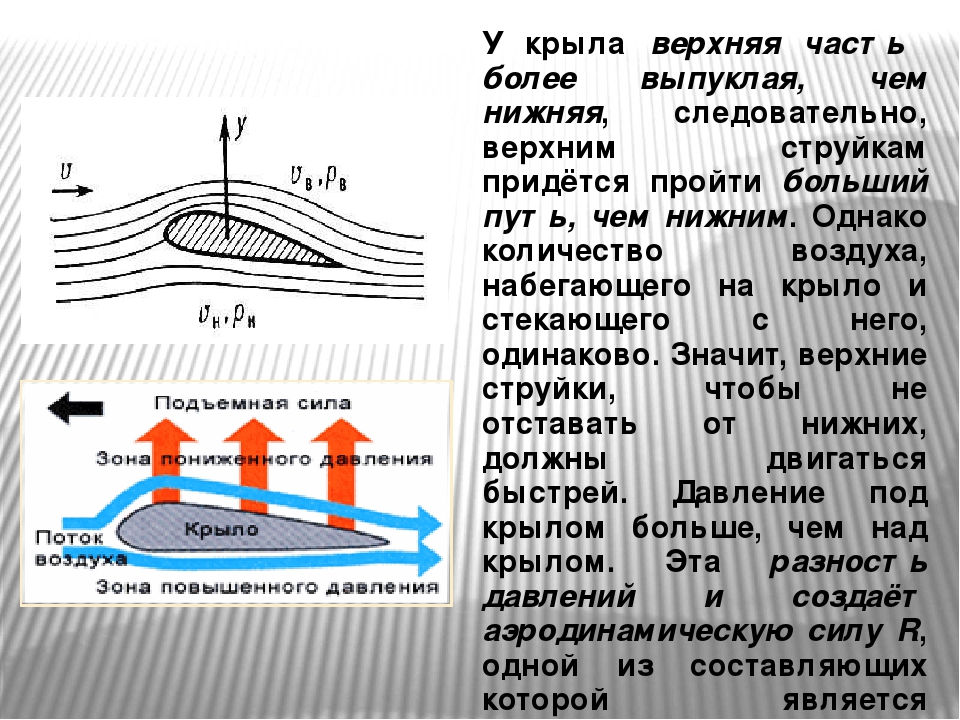 С. А. Чаплыгиным и Н. Е. Жуковским сформулирован упоминавшийся выше постулат, позволяющий устранить неопределенность величины циркуляции, а значит, и подъемной силы. Они обратили внимание на то, что при обтекании тел с заостренной задней кромкой (в частности, при обтекании пластины), согласно теоретическому решению, в точке за-  [c.241]

Поскольку обтекание пластины циркуляционное, то согласно теореме Жуковского на пей возникает поперечная сила, равная р I о I Г. Величина циркуляции Г здесь не определена и в нашей теоретической схеме может быть выбрана произвольно. Однако очевидно, что только одно значение циркуляции может дать истинную величину силы Жуковского, совпадающую с опытной. С, А. Чаплыгиным и Н. Е. Жуковским сформулирован упоминавшийся выше постулат, позволяющий устранить неопределенность величины циркуляции, а значит и подъемной силы. Ими было обраш,ено внимание на то, что при обтекании тел с заостренно задней кромкой (в частности, при обтекании пластины), согласно теоретическому решению, в точке заострения скорость обращается в бесконечность, тогда как при реальном обтекании это физически невозможно. Устранить это несоответствие теоретической схемы опыту можно, выбрав определенное значение циркуляции.  [c.258]

В основе современной теории крыла лежит теорема Жуковского о подъемной силе. Исследуя обтекание тела невязкой жидкостью, Н. Е. Жуковский предложил искать источник силового воздействия на тело в образовании циркуляции скорости, обусловленной наличием вихря. Он получил формулу для определения подъемной силы при безотрывном обтекании произвольного контура несжимаемой жидкостью. М. В. К е л д ы ш и Ф. И. Ф р а н к л ь доказали, что формула Жуковского справедлива и для сжимаемого газа при дозвуковых скоростях течения.  [c.161]

Для примера рассмотрим схему, объясняющую причину появления циркуляции, а следовательно, согласно теореме Н. Е. Жуковского, и возникновения подъемной силы на крыле самолета или на лопасти турбомашины.  [c.94]

Н. Е. Жуковский доказал, что источником подъемной силы крыла является циркуляционное течение жидкости вокруг его профиля (см. рис. 74), возникающее вследствие несимметрии крыла по отношению к скорости набегающего потока, и установил зависимость между подъемной силой и циркуляцией скорости Г  [c.125]

Для определения действительного значения подъемной силы необходимо указать методы определения циркуляции Г. Этот вопрос был изучен и разрешен тоже в работах С. А. Чаплыгина и Н. Е. Жуковского.  [c.85]

Для установившегося потенциального обтекания цилиндрического крыла с циркуляцией, отличной от нуля, Н. Е. Жуковский установил наличие подъемной силы, действующей на профиль крыла (см. 8). Для подъемной силы, действующей на единицу ширины профиля в поперечном направлении, Н. Е. Жуковский получил следующую формулу  [c.300]

Эта формула позволила понять в рамках теории обтекания крыльев идеальной жидкостью механическую природу подъемной силы.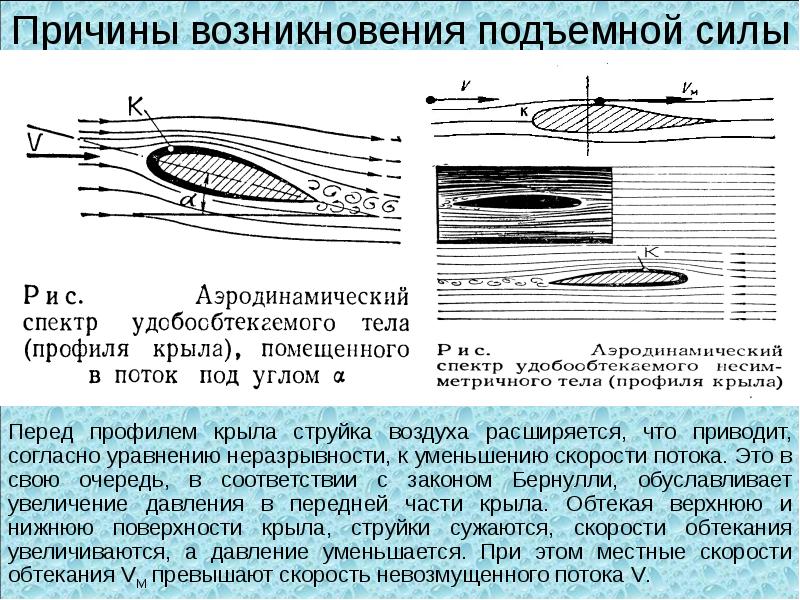 Теорема Н. Е. Жуковского особенно существенна в связи с тем, что при непрерывном установившемся обтекании тел идеальной жидкостью с однозначным потенциалом скорости имеет место парадокс Даламбера, согласно которому полная сила, действующая со стороны жидкости на тело, равна нулю. Открытие наличия подъемной силы, возникающей за счет циркуляции, обусловливающей неоднозначность потенциала скорости, имело большое принципиальное значение.  [c.300]

Русские ученые внесли существенный вклад в дело развития теории газотурбинных установок. Вихревая теория несущего крыла аэроплана, в частности теорема о подъемной силе, закон постоянства циркуляции по радиусу осевой лопаточной машины, разработанные Н. Е. Жуковским (воздушный винт НЕЖ), послужили в дальнейшем фундаментом, на котором создавалась теория профилирования лопаток осевых компрессоров и лопаток газовых турбин. Многоступенчатый осевой компрессор для сжатия воздуха был опубликован впервые в отечественной литературе К.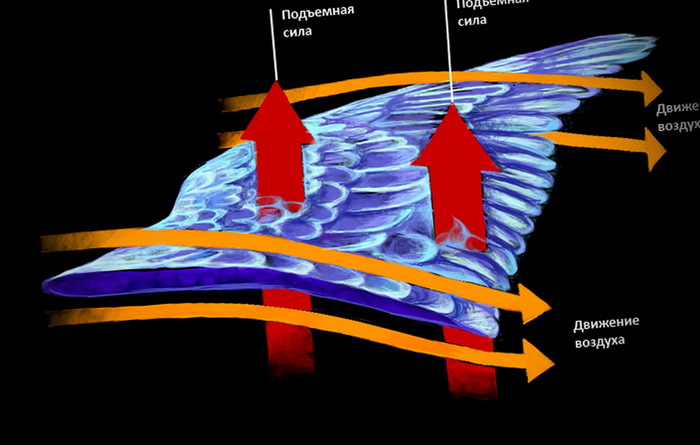 Э. Циолковским в 1930 г.  [c.100]

Первая из формул (83) выражает известную теорему Жуковского о подъемной силе(крыла в плоскопараллельном безвихревом потоке идеальной несжимаемой жидкости. Эта теорема была опубликована в 1906 г. в классическом мемуаре О присоединенных вихрях ), в котором Н. Е. Жуковский впервые установил вихревую природу сил, действующих со стороны потока на крыло, и указал на наличие простой зависимости между этой силой и циркуляцией скорости по контуру, охватывающему обтекаемое крыло.  [c.192]

В начале книги помещены исторические замечания. Редактор и переводчики сочли необходимым пополнить перечень имен ученых, вклад которых в развитие гидродинамики оказал большое влияние на формирование идей и дальнейшее направление развития этой науки. Отметим еще, что, по нашему мнению, в этих замечаниях, подчеркивая заслуги Ланчестера в развитии современного представления о движении жидкости, автор несколько переоценивает роль этого выдающегося исследователя.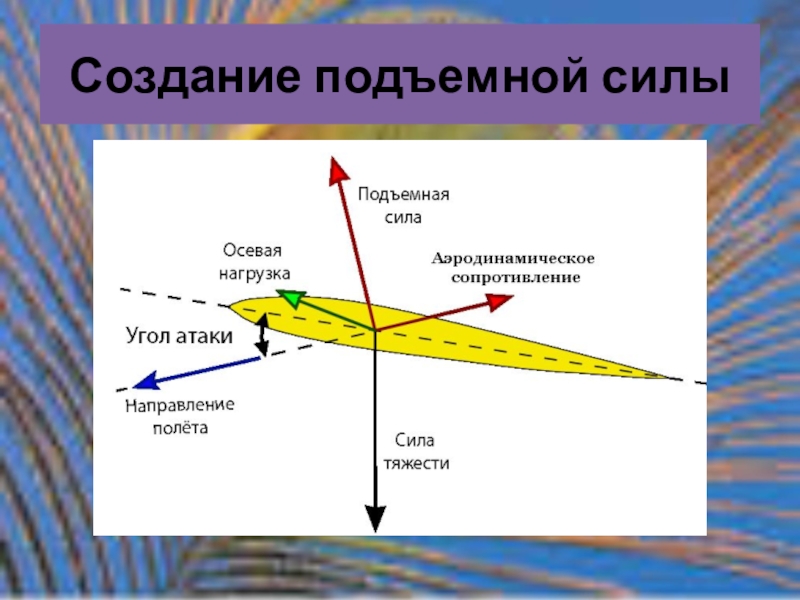 Несмотря на то что с именами Ланчестера и Кутта связаны первые представления о циркуляции как об основной причине возникновения подъемной силы крыла, именно Н. Е. Жуковский создал современное представление об эквивалентности крыла некоторому вихрю. Это представление в сочетании с блестящей по своей простоте и эффективности гипотезой о конечности значений скорости на острой кромке крыла (Н. Е. Жуковский, С. А. Чаплыгин) являются основой современной аэродинамики.  [c.6]

Сила А называется поперечной, или подъемной силой. Соотношение, выражаемое уравнением (56), называется теоремой Жуковского о подъемной силе . Эта теорема может быть доказана также другим путем. Так, например, Н. Е. Жуковский вывел ее, применив теорему о количестве движения к контрольной поверхности в виде круглого цилиндра очень большого радиуса и с осью, совпадающей с осью крыла. При этом одна половина подъемной силы А получается вследствие переноса количества движения, а другая половина как результирующая сил давления. Теорема Жуковского важна прежде всего потому, что она дает возможность вычислить по заданной подъемной силе соответствующую циркуляцию, определяющую напряженность вихря позади крыла.  [c.124]

Решение проблемы подъемной силы было впервые дано проф. Н. Е. Жуковским (1847—1921), чем и было положено начало современной аэродинамике. Один из учеников проф. Н. Е. Жуковского, акад. Л. С. Лейбензон, указывает ), что к идее решения задачи о подъемной силе проф. Жуковский пришел еще осенью 1904 г., но лишь через год сделал доклад о своей работе в Московском Математическом обществе, а опубликовал ее в 1906 г. ). Проф. Жуковский рассматривает непрерывное обтекание профиля крыла, т. е. обтекание без срыва струй с поверхности, и исследует, в чем заключается влияние профиля на окружающую среду. Оказывается, что крыло создает в окружающей среде поток с замкнутыми струйками, окружающими профиль этот поток Жуковский называет циркуляционным и устанавливает, что в нем заключается причина возникновения подъемной силы. Вычисляя подъемную силу, Жуковский выводит свою знаменитую теорему, являющуюся и до настоящего времени основой теории крыла,—теорему о том, что подъемная сила, приходящаяся на единицу длины размаха крыла, равна произведению плотности среды на скорость набегающего потока и на величину, характеризующую циркуляционный поток, называемую циркуляцией скорости.  [c.15]

Н. Е. Жуковский сделал принципиальные открытия в новой науке — аэромеханике, являющейся теоретической основой авиационной техники. Ряд важных законов теоретической аэромеханики был установлен в трудах Жуковского. Он доказал основную теорему о подъемной силе профиля крыла, сформулировал гипотезу для подсчета циркуляции скорости вокруг крыла с острой задней кромкой, предложил серии теоретических профилей крыльев и разработал вихревую теорию воздушного гребного винта (пропеллера). Основные методы аэродинамического эксперимента и широко использованные конструкции аэродинамических труб в нашей стране были созданы под непосредственным руководством Н.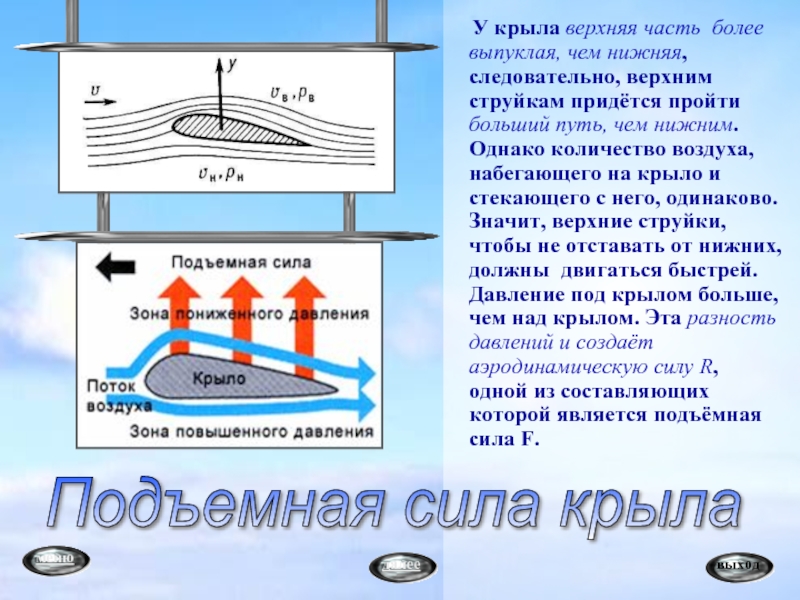 Е. Жуковского. Он первый указал ка применения теоретической и экспериментальной аэродинамики к задачам расчета летных характеристик самолета. Аэродинамический расчет и динамика самолетов как самостоятельные научные дисциплины были начаты работами Жуковского. В. И. Ленин назвал Жуковского отцом русской авиации .  [c.37]

Связь величины подъемной силы с циркуляцией скорости была впервые установлена Н. Е. Жуковским, и полученная им теорема о подъемной силе называется теоремой Жуковского.  [c.302]

Одним из важных, ставшим теперь классическим, является раздел аэродинамики, изучающий обтекание профиля плоским потоком идеальной несжимаемой жидкости. Этот раздел имеет и первостепенное прикладное значение, являясь основой изучения дозвукового обтекания крыла и многих других вопросов гидро- и аэродинамики. Законы, характеризую—щие обтекание профиля идеальной несжимаемой жидкостью, были установлены в получивших всеобщее признание работах Н. Е. Жуковского и С, А, Чаплыгина. Сюда, прежде всего, относятся теорема Жуковского о подъемной силе, связавшая величину подъемной силы с циркуляцией скорости вокруг профиля, и условие Чаплыгина — Жуковского, дающее возможность зафиксировать величину циркуляции, исходя из предположения о единственной физически возможной схеме безотрывного обтекания  [c.85]

В 1905—1910 гг. появляются блестящие работы Н. Е. Жуковского, в которых он впервые объяснил природу возникновения подъемной силы, поддерживающей летящий самолет в воздухе. В 1905 г. Н. Е. Жуковский докладывает Московскому математическому обществу свою теорему о связи между подъемной силой и циркуляцией. Это открытие обессмертило имя Н. Е. Жуковского.  [c.14]

Чтобы найти ур-ие связи крыла с потоком, воспользуемся теоремой Н. Жуковского, по к-рой подъемная сила через циркуляцию выражается следующим образом  [c.56]

Используя найденный закон распределения циркуляции в виде ряда, можно определить скос потока и соответствующие аэродинамические коэффициенты [16].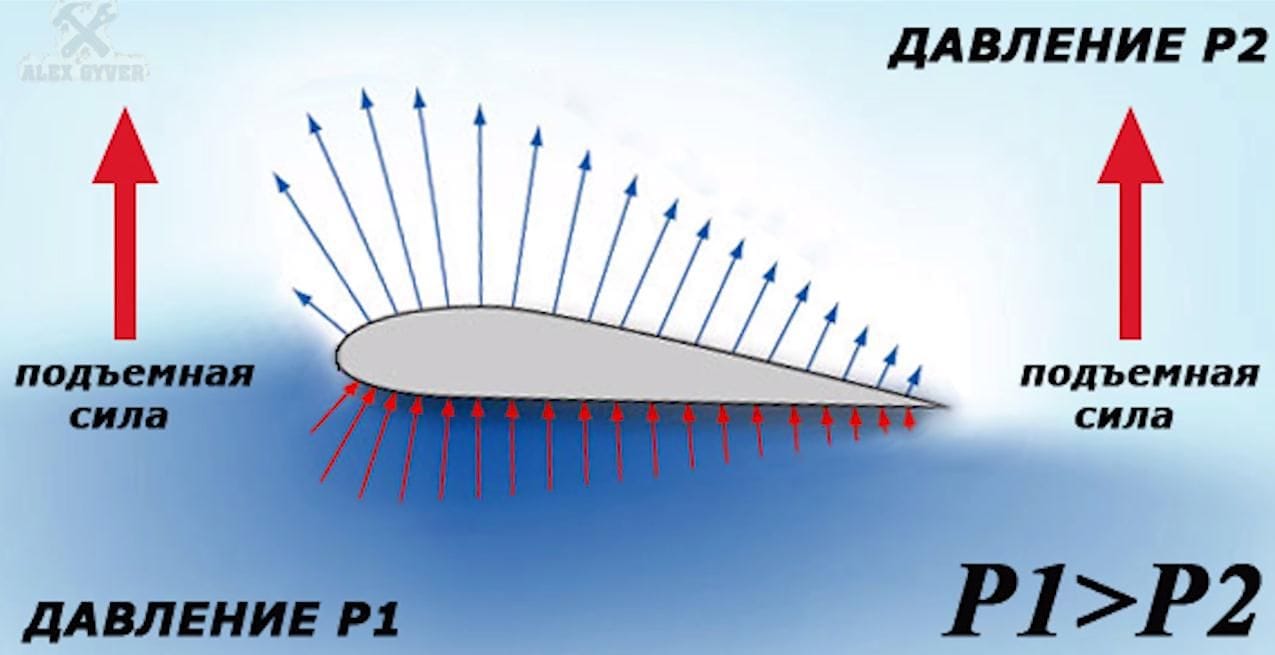 Переходя в (6.4.6″)от переменной z к новой переменной 6 в соответствии с выражением az= = (//2) sin ede. подставляя формулу для циркуляции в виде ряда н заменяя /V-Skp на Я р. найдем зависимость для коэффициента подъемной силы  [c.249]

Выдающаяся роль в разработке теории обтекания тел потоком, имевшей исключительно важное значение для развития авиации, принадлежит Н.Е.Жуковскому. Он показал, что подъемная сила крыла связана с вихрем, названным им присоединенным, обтекающим крыло. Основная идея расчета подъемной силы сводится к следующему. Если бы в воздухе отсутствовали силы вязкости, то картина обтекания крыла была бы такой, как на рис. 4.28(й). Подъемная сила, однако, будет равна нулю, поскольку поток позади крыла не изменил направления движения. Обтекание крыла реальным воздухом, изображенное на рис. 4.28(в), может рассматриваться как суперпозиция невязкого обтекания (а) и вихревого движения воздуха вокруг крыла самолета по часовой стрелке (б). Величина подъемной силы напрямую связана с наличием циркуляции скорости Г (4. 24) по контуру, охватывающему крыло самолета. Этот контур должен находиться вне пограничного слоя (б), толщина которого для движущегося с дозвуковой скоростью самолета составляет несколько сантиметров. Из закона сохранения момента импульса следует, что позади крыла должны образовываться вихри с движением в них воздуха против часовой стрелки. На рис. 4.29 представлена фотография вихревой дорожки, образующейся при обтекании модели крыла самолета. Эта цепочка вихрей появляется потому, что при отрыве от крыла одного вихря циркуляция  [c.82]

Использование теории о связи подъемной силы с циркуляцией и схемы модели течения с присоединенным вихрем, данных Н. Е. Жуковским, позволило развить теорию индуктивного сопротивления, теорию крыла конечного размаха, теорию воздушного винта — важнейшие разделы практической аэродинамики, разработанные в основном в течение этого периода и явившиеся логическим продолжением и развитием идей составляющих фундамент теории крыла бесконечного размаха.  [c.284]

Теорема Н. Е. Жуковского. При обтекании прямолинейной плоской решетки несжимаемой идеальной жидкостью на профиль действует только сила Жуковского (подъемная сила), направленная по нормали к вектору средней геометрической скорости. Для определения направления силы Жуковского следует вектор средней геометрической скорости повернуть на 90° в сторону, противоположную направлению циркуляции скорости.  [c.362]

По теореме проф. Н. Е. Жуковского подъемная сила возникает только в том случае, если вокруг крыла имеется циркуляция. Подъемная сила Р определяется по уравнению  [c.18]

Это условие, сформулированное Н. Е. Жуковским и С. А. Чаплыгиным, позволяет вычислять циркуляцию Г и вместе с тем подъемную силу крыла.  [c.23]

Формула (3-40) выражает теорему Н. Е. Жуковского, являющуюся основной теоремой аэродинамики. Теорему Жуковского можно сформулировать так при обтекании тела плоскопараллельным безграничным потоком идеальной сжимаемой жидкости на тело единичного размаха действует сила, равная произведению циркуляции скорости Г на скорость и на плотность Роо невозмущенного потока. Направление этой силы нормально к направлению скорости невозмущенного потока с . При этом, как следует из вывода, если циркуляция скорости, вычисленная при обходе по часовой стрелке, окажется положительной, то и будет положительной. Подъемную силу часто называют силой Жуков-  [c.97]

Н.Е.Жуковский доказал, что источником подъемной силы крыла является циркуляционное движение потока вокруг его профиля и установил зависимость между подъемной силой Ку и циркуляцией скорости Г, которая имеет вид  [c.152]

Развитие авиации требовало создания теории крыла, и эта теория обязана своим возникновением фундаментальным работам Н. Е. Жуковского (1847—1921) и С. А. Чаплыгина (1869—1942). В 1906 г. Н. Е. Жуковский в Po iHi, а за рубежом Кутта п Ланчестер опубликовали теорему о подъемной силе крыла, а позднее Н. Е. Жуковский совместно с С. А. Чаплыгиным сформулировал постулат о плавном обтекании его задней кромки, позволивший вычислять циркуляцию скорости,, возникающую вокруг крылового профиля. Последующие публикации С. А. Чаплыгина и Н. Е. Жуковского по теории крыла уже к 1910—1911 гг. практически закончили цикл этих исследований, так как были даны не только формулы, но и методы построения крыловых профилей, названных в последствии именами их авторов.  [c.11]

Результат этой работы представляет значительный интерес как косвенное подтверждение теории, предложенной Н.Е. Жуковским и объясняюгцей образование подъемной силы возникновением циркуляции вокруг крыла или возникновением нрисоединенных вихрей.  [c.170]

Доказав теорему о подъемной силе крыла, Н. Е. Жуковский [1.3J инсрпые дал рааьяснение механизма образования подъемной силы. Он показал, что подъемная сила при безотрывном обтекании в стационарном потоке идеальной жидкости возникает благодаря появлению циркуляции скорости по замкнутому контуру, охватьшающему сечение тела. Таким образом был разъяснен и парадокс Эйлера—Даламбера о равенстве нулю реакции потока идеальной несжимаемой жидкости на тело при его установившемся прямолинейном движении. Эта реакция действительно отсутствует, если указанная циркуляция равна 1 улю. И. Е. Жуковский установил возможность изучения несущих свойств крыльев в идеальной среде путем построения неоднозначных потенциальных течений. Важную роль в создании современных вычислительных методов сыграло также введенное им понятие о присоединенных вихрях.  [c.11]

Мысль связать подъемную силу крыла с циркуляцией зародилась одновременно у многих ученых. Источник ее можно искать еще в попытках Рэлея (1878) объяснить эффект Магнуса. Качественно эта связь впервые была осознана, по-видимому, Ф. Ланчестером, который не смог ей, однако, придать количественного выражения. К математическому выражению этой идеи подошли независимо Н. Е, Жуковский и В. Кутта. Жуковскому принадлежит первая публикация содержаш,ая по суш,еству знаменитую формулу подъемной силы Р = pFT (р — плотность воздуха, Г — циркуляция скорости вокруг обтекаемого потоком тела, V — скорость движения тела). Следующий принципиальный шаг в определении подъемной силы заключался в установлении способа нахождения циркуляции скорости вок руг крыла, исходя из условия плавного схождения потока с задней его заостренной кромки. Этот шаг сделали В. Кутта и С. А. Чаплыгин . Тем самым были 289 заложены основы аэродинамики крыла бесконечного размаха.  [c.289]

Здесь я хочу обратить внимание, что результат этой теории, которую мы называем теорией циркуляции подъемной силы, значительно отличается от теории Ньютона. В теории Ньютона предполагается, что отклоняемая возд гн1пая масса — это количество воздуха, который непосредственно сталкивается с поверхностью тела. Если хорда плоской пластины L, а угол атаки а, то масса воздуха, которая отклоняется па единицу ширины пластины, пропорциональна Lsina (рнс. 5, стр. 20). Однако в соответствии с теорией циркуляции, она пропорциональна 3,14L. Например, если а составляет 5°, при этом sin а меньше 0,1, то результат Ньютона ошибочен более, чем на множитель 30. Сравненне между результатом Ньютона н теорией циркуляции также можно увидеть на рис. 14 (стр. 35), где построен график зависимости безразмерной перпендикулярной силы (т. е. составляюш,ей силы, перпендикулярной пластине тогда как подъемная сила является состав-ляюгцей, перпендикулярной направлению относительного потока) от угла атаки.  [c.54]

Н. Е. Жуковский является основоположником учения о подъемной силе крыла в илоскопараллельном потоке. Знаменитая формула Жуковского, выражающая подъемную силу крыла в виде произведения плотности жидкости на скорость движения в ней крыла и на напряжение присоединенных вихрей или циркуляцию , опубликованная п 1906 г., получила всеобщее признание как основа теории подъемной силы крыла. Зарубежные историки аэродинамики пытаются без достаточных к тому оснований поделить приоритет Жуковского на эту формулу с немецким ученым Кутта, работа которого по вопросу о подъемной силе частного вида крыла была опубликована несколько ранее работы Жуковского. При этом затушевывается тот основной исторический факт, ч го только Жуковский дал первую общую теорию подъемной силы, основанную на смелой и оригинальной идее присоединенного вихря . Приоритет на циркуляционную теорию подъемной силы великого русского ученого, далеко продвинувшего вперед разрешение почти всех основных гидроаэродинамических проблем своего времени и открывшего новые пути развития современной механики жидкости и газа, совершенно неоспорим.  [c.30]

Предполагается, что все нули производной dzld лежат внутри круга, кроме одного, расположенного на окружности в точке J= —/= 6 —ае здесь а, Ь н / — действительные числа коэффициенты а , вообще говоря, считаются комплексными числами. Кроме того, пусть циркуляция вокруг профиля выбрана в соответствии с постулатом Чаплыгина-Жуковского. Показать, что иа крыло, помещенное в рассматриваемое течение, действует подъемная сила, направленная перпендикулярно к скортсти в бесконечности и обращающаяся в нуль при некоторых углах атаки. Найти выражение для О] из условия, чтобы момент относительно центра круга обращался в нуль вместе с подъемной силой.  [c.194]

Другим примером потенциального потока с циркуляцией является поток около крыла самолета (рис. 63). Этот поток получатся из обычного потенциального потока без циркуляции (рис. 64) путем наложения на последний циркуляционного потока, изображеннго на рис. 65, вследствие чего при обтекании крыла также возникает циркуляция. С циркуляцией тесно связано возникновение подъемной силы крыла. Без всякого расчета легко видеть, что при наложении циркуляционного потока на обычный потенциальный поток (рис. 64) скорость последнего над крылом увеличивается, а под крылом, наоборот, уменьшается. Согласно уравнению Бернулли это означает, что над крылом давление уменьшается, а под крылом увеличивается, следовательно, возникает сила, действующая на крыло снизу вверх, т.е. подъемная сила. Кут-та (Ки11а) и Н. Е. Жуковский независимо друг от друга нашли путем теоретических расчетов, что подъемная сила на единицу длины крыла равна  [c.104]

Если в формулу (203) подставить I и и, определенные из эксперимента, тогда вычисленные значения Сх вихр хорошо согласуются со значениями Сх вихр, определенными непосредственны-ми замерами сил лобового сопротивления на аэродинамических весах. Следовательно, формула Кармана (203) схватывает правильно суть явления, но нуждается в дополнительных соотношениях, устанавливающих связь геометрических параметров контура с кинематическими и геометрическими параметрами шахматной системы вихрей. Пользуясь аналогией, можно сказать, что формула Кармана (203) играет в теории лобового сопротивления (построенной в рамках представлений идеальной жидкости) ту же роль, что и формула Н. Е. Жуковского в теории подъемной силы. Мы указывали, что практическое значение формула Жуковского обрела лишь тогда, когда был указан прием определения циркуляции присоединенного вихря, т. е. формулирована гипотеза Жуковского о конечности скорости частиц жидкости у задней острой кромки профиля крыла. Построение соответствующих физических гипотез, позволяющих прилагать теорию вихревого сопротивления к решению конкретных  [c.361]

Теорию крыла конечного размаха позволило создать использование основополагающей теоремы Н. Е. Жуковского о связи подъемной силы с циркуляцией и модели течения с присоединенным вихрем, так что эта теория является логическим продолжением и развитием идей, составляющих фундамент теории крыла бесконечного размаха, В 1910 г. С. А. Чаплыгин в докладе на тему Результаты теоретических исследований о, движении аэропланов сформулировал общие представления о вихревой системе крыла конечного размаха.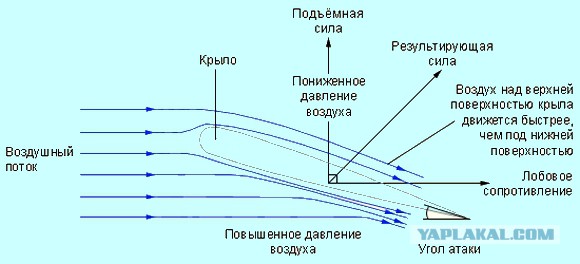 В 1913 и 1914 гг. им были получены первые формулы для подъемной силы и индуктивного сопротивления. Они были доложены на третьем воздухоплавательном съезде в Петербурге. В дальнейшем основное распространение получила теория несущей линии, предложенная в Германии Л. Прандтлем для крыльев большого относительного удлинения. В рамках этой схемь было получено интегро-дифференциальное уравнение, связывающее изменение циркуляции и индуктивный скос потока. Задача свелась к отысканию различных приближенных методов его решения. В работе Б. Н. Юрьева (1926) был применен геометрический прием, в котором использовалось предположение о том, что распределение циркуляции близко к эллиптическому и что отклонения от этого распределения повторяют форму крыла в плане. Аналитические методы, применявшиеся на начальном этапе развития теории для получения приближенных решений, состояли в требовании удовлетворения основному уравнению в ограниченном числе точек по размаху. Так, в методе тригонометрических разложений В. В. Голубев (1931) заменил бесконечный тригонометрический ряд тригонометрическим многочленом, сведя бесконечную систему уравнений к конечной системе, в которой число неизвестных соответствует числу членов разложения циркуляции и числу точек на крыле. С целью более точного учета формы крыла в плане при ограниченном числе решаемых алгебраических уравнений Я. М. Серебрийский (1937) предложил для решения интегро-дифференциального уравнения использовать способ наименьших квадратов.  [c.92]

В. В. Голубева (1935), в которой делалась попытка учесть обтекание боковых кромок крыла с помощью представления о поперечной циркуляции . Создание точной нелинейной теории крыла конечного размаха связано с большими трудностями, которые обусловлены существенным влиянием вязкости и отрыва на этих режимах. Поэтому для приближенных расчетов нелинейных характеристик обычно используются полуэмпирические методы, критерием применимости которых является согласие с результатами испытаний в некотором диапазоне геометрических параметров, таких как форма крыла в плане, угол атаки и т, п, В работе Г, Ф, Бураго (1944) вихревая поверхность заменяется одним несущим вихрем и граничные условия удовлетворяются по хорде в среднем. Угол скоса свободных вихрей принимается равным половине угла атаки приводится приближенная формула для коэффициента подъемной силы, из которой следует его квадратичная зависимость от угла атаки для очень малых удлинений, Н, Н. Поляхов и А, И. Пастухов (1959) дали возможность оценить не только подъемную силу, но и момент. У них крыло заменяется системой П-образных вихрей, причем угол скоса свободных вихрей цринимается равным углу атаки. С, Д, Ермоленко (1960) принял углы скоса П-образных вихрей на концах прямоугольного крыла равными индуктивным углам скоса потока от присоединенных и свободных вихрей. Метод обобщается им на случай крыла малого удлинения вблизи земли, К. К. Федяевский (1949) разработал приближенную теорию крыльев малого удлинения прямоугольной и эллиптической формы в плане, которая позволяет оценить не только подъемную силу и продольный момент, но также приращение  [c.96]

Течение с циркуляцией вокруг крыла, остающееся после уплывания начального вихря, действует нз крыло с результирующей силой, которая дает составляющую, перпендикулярную к направлению натекания. То же самое получается и в случае вращающегося цилиндра. Рассматривая спектр линий тока, мы видим, что над цилиндром линии тока располагаются чрезвычайно тесно, внизу же цилиндра расстояния между отдельными ли-[ иямн тока значительно больше. Следовательно, над цилиндром мы имеем большие скорости, под цилиндром — малые скорости. Применяя уравнение Бернулли, что мы вполне можем сделать для всей области течения вне пограничного слоя, получаем, что над цилиндром имеет место понижение давления, а под цилиндром, наоборот, повышение давления, следовательно, н,н-линдр подвергается со стороны жидкости действию силы, перпендикулярной к направлению натекания, т. е. получает подъемную силу. Это есть так называемый эффект Магнусз. Так как подъемная сила пропорциональна циркуляции (см. № 104), то она в сильной степени зависит от  [c.103]

Вернемся опять к фиг. 14 , на котор.зй изображено течение вокруг окружности с центром в точке г/, проходящей через точки — а и -1 а, причем плоскость г повернута по часовой стрелке на угол а. Наложим на это течение циркуляционное течение, причем величину циркуляции подберем так, чтобы задняя (правая) кри тическая точка оказалась как раз в точке Н- а. Если теперь отобразить при помощи функции (3) плоскость г на плоскость то обтекаемая окружность перейдет в дугу окружности, расположенную косо по отношению к течению, а течение вокруг окружности — в течение вокруг этой круговой дуги. При этом величина циркуляции подбирается так, чтобы задняя критическая точка на плоскости г отобрази-.чась в задний конец круговой дуги на плоскости С, т. е. чтобы не было обтекания задней кромки ребра. Если бы изогнутая пластинка или ее хорда имела больший угол атаки, то для достижения гладкого обтекания заднего ребра необходимо было бы взять большую циркуляцию, что находится в полном согласии с опытом именно, при увеличении угла атаки возрастает подъемная сила, а с нею и циркуляция. Изображенное на фиг. 148 течение вокруг пластинки, изогнутой по дуге круга и наклоненной относительно направления натекания, уже довольно близко напоминает течение вокруг крыльев, применяемых на практике, если только не считать обтекания передней кромки.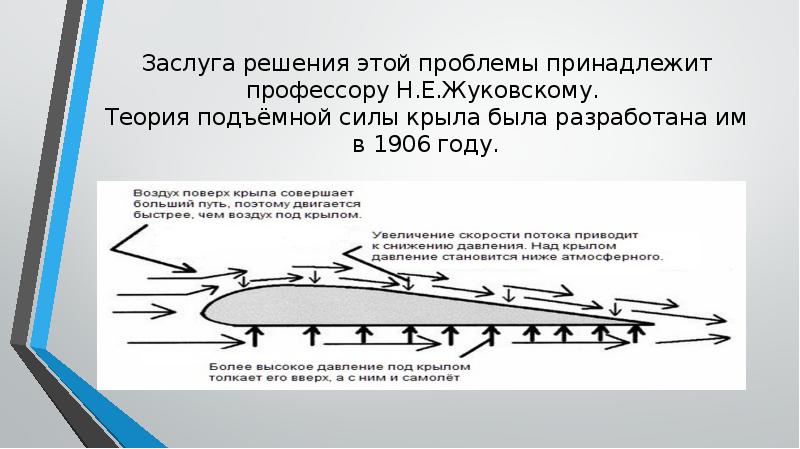  [c.189]

Опыт показывает, что на крыле конечного размаха, например на крыле самолета, циркуляция не сохраняется вдоль размаха, а достигает своего максимального значения посередине крыла и обращается в нуль на его концах. Объясняется это возможностью выравнивания давлений на иижней и верхней поверхностях крыла за счет возникающих перетеканий воздуха на концах крыла из области повышенного давления на нижней поверхностн в область разрежения на верхней. Выравнивание давлений приводит к исчезновению подъемной силы, а следовательно, и циркуляции присоединенного вихря на концах крыла. Наличие перетекания воздуха с нижней поверхности на верхнюю образует на крыле поперечные течения, которые смываются с его поверхности набегающим потоком н, сходя с задней кромки крыла, образуют вихри.  [c.389]

Подъемная сила. Потенциальный поток с циркуляцией около погруженного в него тела можно представить как сумму потенциального потока без циркуляции (рис. XIX. 31,а) и циркуляционного потока (рис. XIX. 31,6). Без осо бых расчетов ясно, что при наложении циркуляционного потока на обычный потенциальный поток окорость последнего над телом узелнчивается (скорости обоих потоков направлены в одну сторону), а под телом, нао-борот, уменьшается. Потому в соответствии с уравнением Д. Бернулли можно утверждать, что давление над телом уменьщается, а под телом увеличивается. Следовательно, возникает сила, действующая на тело вверх,—по Н. Е. Жуковскому, подъемная сила. В 1904 г. П. Е. Жуковский одновременно с Куттом, но независимо от него, доказал теорему о подъемно й силе, которую обычно называют теоремой Жуковского —Кутта  [c.422]

В течение ряда лет, после получения Н. Е. Жуковским формулы подъемной силы J = Qoofl7циркуляции скорости Г (см. п. 3.5) вокруг профиля и методы расчета ее величины. В 1908 г. Н. Е. Жуковский и С. А. Чаплыгин сформулировали свой знаменитый постулат.  [c.343]

---

Подъемная сила крыла самолета

УПРАВЛЕНИЕ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ ИЧАЛКОВСКОГО МУНИЦИПАЛЬНОГО РАЙОНА

Конкурс по физике

«ФИЗИКА ВОКРУГ НАС»

ФИЗИЧЕСКИЙ ЭКСПЕРИМЕНТ

ПОДЪЕМНАЯ СИЛА КРЫЛА САМОЛЕТА

Яманов Виктор

МОУ «Тархановская СОШ», с.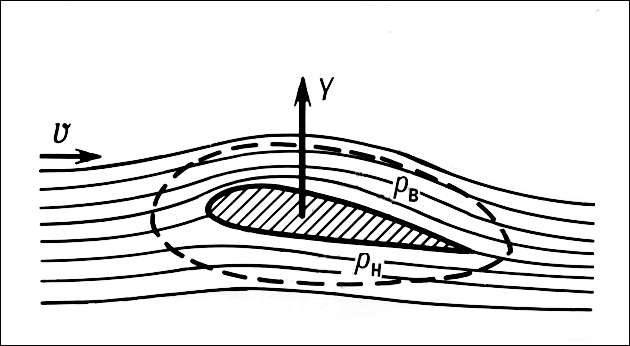 Тарханово, 9 класс

Руководитель:

Аверкин Иван Андреевич,

учитель физики и математики

МОУ «Тархановская СОШ»

Ичалковского муниципального района Республики Мордовия

2011

Оглавление

Введение ………………………………………………………………….

4

Почему и как возникает подъемная сила

5

Подъемная сила крыла самолета.

6

Физический эксперимент

7

Аэродинамика крыла самолета

8

Заключение

10

Литература. ………………………………………….

12

Введение

Почему могут летать птицы несмотря на то что они тяжелее воздуха? Какие силы поднимают огромный пассажирский самолет, который может летать быстрее, выше и дальше любой птицы, ведь крылья его неподвижны? Почему планер, не имеющий мотора, может парить в воздухе? На все эти и многие другие вопросы дает ответ аэродинамика — наука, изучающая законы взаимодействия воздуха с движущимися в нем телами.

В развитии аэродинамики у нас в стране выдающуюся роль сыграл профессор Николай Егорович Жуковский (1847 —1921) — «отец русской авиации». Заслуга Жуковского состоит в том, что он первый объяснил образование подъемной силы крыла и сформулировал теорему для вычисления этой силы. Им была решена и другая проблема теории полета — объяснена сила тяги воздушного винта.

Жуковский не только открыл законы, лежащие в основе теории полета, но и подготовил почву для бурного развития авиации в нашей стране. Он связал теоретическую аэродинамику с практикой авиации, дал возможность инженерам использовать достижения ученых-теоретиков. Под научным руководством Жуковского были организованы Аэрогидродинамический институт (сейчас ЦАГИ), ставший крупнейшим центром авиационной науки, и Военно-воздушная академия (сейчас ВВИА им. проф. Н. Е. Жуковского), где подготавливают высококвалифицированные инженерные кадры для авиации.

Основным приспособлением, служащим для изучения законов движения тел в воздухе, является аэродинамическая труба. Простейшая аэродинамическая труба представляет собой профилированный канал. В одном конце трубы установлен мощный вентилятор, приводимый во вращение электродвигателем. Когда вентилятор начинает работать, в канале трубы образуется воздушный поток. В современных аэродинамических трубах можно получать различные скорости воздушного потока вплоть до сверхзвуковых. В их каналах можно помещать для исследования не только модели, но и реальные самолеты.

Важнейшими законами аэродинамики являются закон сохранения массы (уравнение неразрывности) и закон сохранения энергии (уравнение Бернулли).

Рассмотрим природу возникновения подъемной силы. Опыты, проведенные в аэродинамических лабораториях, позволили установить, что при набегании на тело воздушного потока частицы воздуха обтекают тело. Картину обтекания тела воздухом легко наблюдать, если поместить тело в аэродинамической трубе в подкрашенном потоке воздуха, кроме того, ее можно сфотографировать. Полученный снимок называют спектром обтекания.

Упрощенная схема спектра обтекания плоской пластинки, поставленной под углом 90° к направлению потока, изображена на рисунке.

Простейшими летательными аппаратами яв­ляются бумажные змеи, которые запускают уже несколько тыся­челетий и для забавы, и для научных исследований. Изобре­татель радио А. С. Попов с помощью бумажного змея поднимал проволоку (антенну) для увеличения дальности радиопередачи.

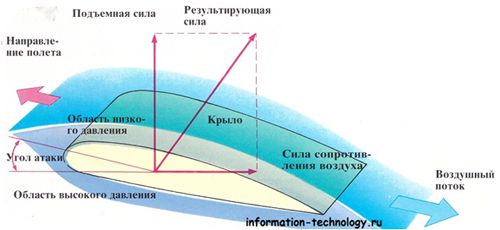
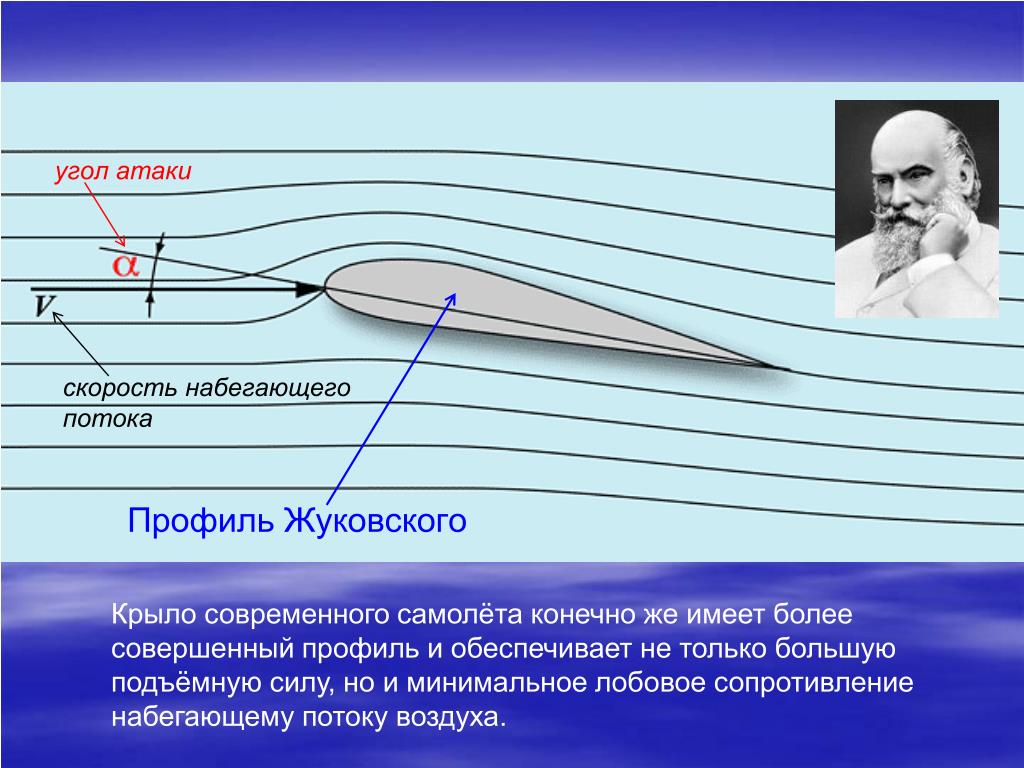
Змей представляет собой плоскую пластину, расположенную под углом α к направлению потока воздуха. Этот угол получил название угла атаки. При взаимодействии этой пластины с потоком возникает подъемная сила F_n, являющая­ся вертикальной составляющей силы R, действующей со стороны потока на пластину.

Механизм возникновения силы R двоякий. С одной стороны, это сила реакции, возникающая при отражении потока воз­духа и равная изменению его импульса в единицу времени

С другой стороны, при обтекании пластины за ней образуются вихри, понижающие, как это следует из уравнения Бернулли, давление над пластиной.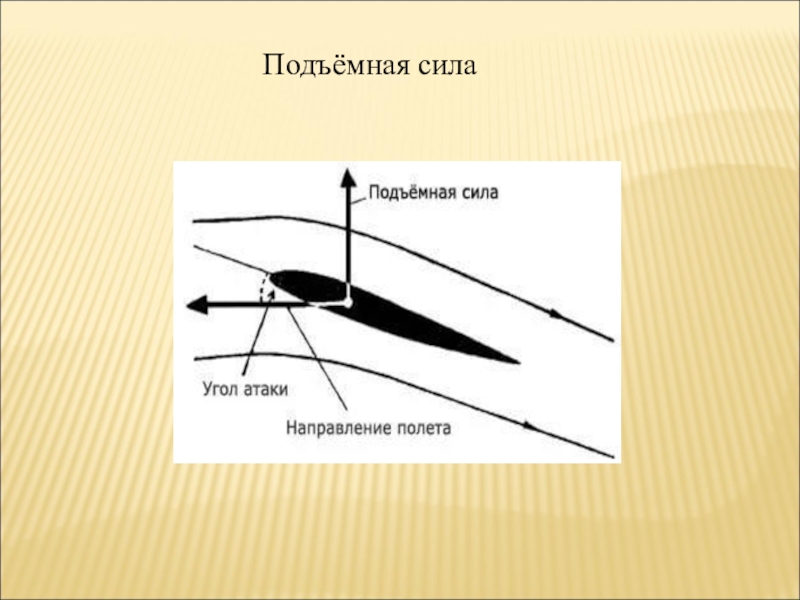

Горизонтальная составляющая силы R является силой со­противления давления F_с. График зависимости подъемной силы и силы сопротивления от угла атаки изображен на рисунке, из которого видно, что максимальная подъемная сила дости­гается при угле атаки, равном 45°.

Уравнение Бернулли позволяет рассчи­тать подъемную силу крыла самолета при его полете в воздухе. Если скорость потока воздуха над крылом v₁ ока­жется больше скорости потока под кры­лом v₂, то согласно уравнению Бернулли возникает перепад давлений:

где р₂ — давление под крылом, р₁ -давление над крылом. Подъемную силу можно рассчитать по формуле

где S — площадь поверхности крыла, v₁ — скорость пото­ка воздуха над крылом, v₂ — скорость потока воздуха под крылом.

Возникновение подъемной силы при существовании различия в скоростях движения потока воздуха, обтекающего тело, можно продемонстрировать следующим опытом.

Закрепим модель крыла в аэродинамических весах и будем продувать воздух с помощью аэродинамической трубы или пы­лесоса. Чтобы найти подъемную силу, можно с по­мощью микроманометра измерить статическое давление воздуха над крылом р₁ и под крылом р₂. Рассчитанное по формуле F_n= =(p₂—p₁)S значение подъемной силы совпадает с показания­ми шкалы аэродинамических весов.

Физический эксперимент

Приборы и оборудование для эксперимента:

1. Вентилятор бытовой

2. Микроманометр

3. Макет крыла

4. Штатив

5. Лист бумаги

Вычисления

Р₁ = -2 мм вод. ст.

Р₂ = 1 мм вод. ст.

∆Р = Р₂ – Р₁ = 1- (-2) = 3 мм вод. ст.

∆Р = ρgh = 1000 ∙ 10 ∙ 3 10^-3 = 30 Па

F_п = Р₂ ∙ S – Р₁ ∙ S = S ∙ ∆Р = 18 ∙ 26 ∙ 10^-4 ∙ 30 = 468 ∙ 30 ∙ 10^-4 ≈

≈ 1,4 Н

Р = F_Т = 0,5 Н.

Аэродинамика крыла самолета

При обтекании воздушным потоком крыла самолета верхняя и нижняя части потока воздуха из-за несимметричности формы крыла проходят различные пути и встречаются у задней кромки крыла с различными скоростями.

Это приводит к возникно­вению вихря, вращение которого происходит против часовой стрелки.

Вихрь обладает определенным моментом импульса. Но по­скольку в замкнутой системе момент импульса должен оставать­ся неизменным, вокруг крыла возникает циркуляция воздуха, направленная почасовой стрелке.

Обозначив скорость потока воздуха относительно крыла че­рез и, а скорость циркуляционного потока через и, преобразуем выражение для подъемной силы крыла самолета:

где v₁ = u + v, u₂=u—v. Тогда

Такую формулу в 1905 г. впервые получил Николай Егоро­вич Жуковский

Н. Е. Жуковский установил профиль поперечного сечения крыла с максимальной подъемной силой и минимальной силой лобового сопротивления. Он создал также вихревую теорию винта самолета, нашел оптимальную форму лопасти винта и рассчитал силу тяги пропеллера.

Поперечное сечение крыла плоскостью, параллельной плоскости его симметрии называется «профилем». Типовой профиль крыла выглядит так:

Максимальное расстояние между крайними точками профиля – b , называется хордой профиля. Наибольшая высота профиля – c , называется толщиной профиля.

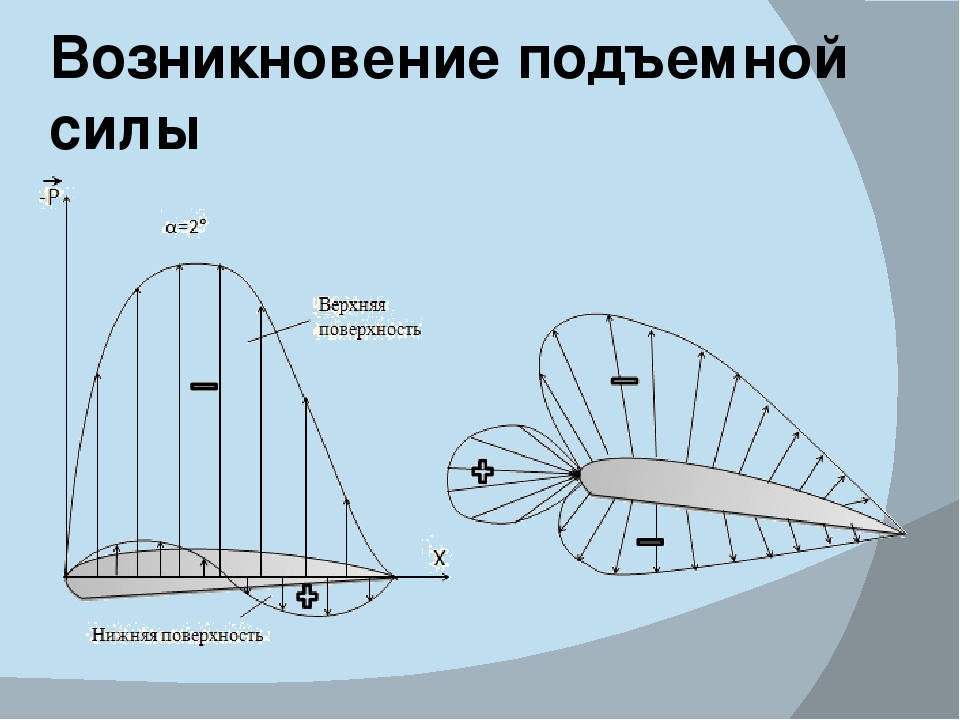
Подъемная сила крыла возникает не только за счет угла атаки, но также и благодаря тому, что поперечное сечение крыла представляет собой чаще всего несимметричный профиль с более выпуклой верхней частью.

Крыло самолета или планера, перемещаясь, рассекает воздух. Одна часть струек встречного потока воздуха пойдет под крылом, другая — над ним.

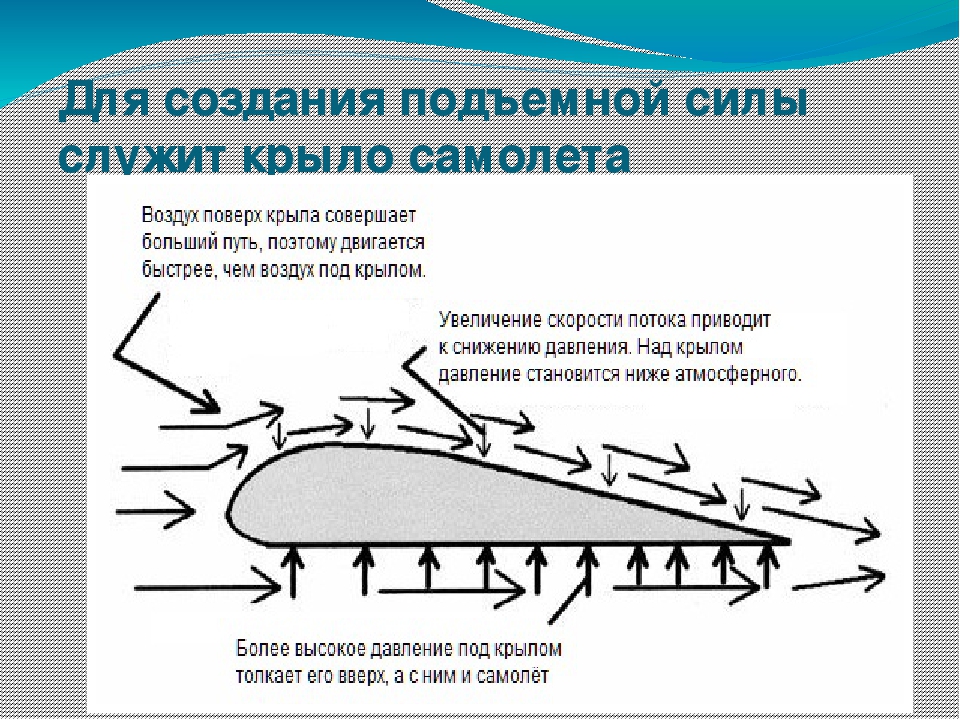
У крыла верхняя часть более выпуклая, чем нижняя, следовательно, верхним струйкам придется пройти больший путь, чем нижним. Однако количество воздуха, набегающего на крыло и стекающего с него, одинаково. Значит, верхние струйки, чтобы не отстать от нижних, должны двигаться быстрее.

Линии течения элементарных струек воздуха обозначены тонкими линиями. Профиль к линиям течения находится под углом атаки а – это угол между хордой профиля и невозмущенными линиями течения. Там, где линии течения сближаются, скорость потока возрастает, а абсолютное давление падает. И наоборот, где они становятся реже, скорость течения уменьшается, а давление возрастает. Отсюда получается, что в разных точках профиля воздух давит на крыло с разной силой.

В соответствии с уравнением Бернулли, если скорость воздушного потока под крылом меньше, чем над крылом, то давление под крылом, наоборот, будет больше, чем над ним. Эта разность давлений и создает аэродинамическую силу R,

На рисунке дано схематическое изображение спектра обтекания пластинки, поставленной под острым углом к потоку. Под пластинкой давление повышается, а над ней вследствие срыва струй получается разрежение воздуха, т. е. давление понижается. Благодаря образующейся разности давлений и возникает аэродинамическая сила. Она направлена в сторону меньшего давления, т. е. назад и вверх. Отклонение аэродинамической силы от вертикали зависит от угла, под которым пластинка поставлена к потоку. Этот угол получил название угла атаки (его принято обозначать греческой буквой а — альфа).

Заключение

Свойство плоской пластинки создавать подъемную силу, если на нее набегает под острым углом воздух (или вода), известно уже с давних времен. Примером тому служит воздушный змей и руль корабля, время изобретения которых теряется в веках.

Чем больше скорость набегающего потока, тем больше и подъемная сила и сила лобового сопротивления. Эти силы зависят, кроме того, и от формы профиля крыла, и от угла, под которым поток набегает на крыло (угол атаки), а также от плотности набегающего потока: чем больше плотность, тем больше и эти силы. Профиль крыла выбирают так, чтобы оно давало возможно большую подъемную силу при возможно меньшем лобовом сопротивлении.

Теперь мы можем объяснить, как летает самолет. Воздушный винт самолета, вращаемый двигателем, или реакция струи реактивного двигателя, сообщает самолету такую скорость, что подъемная сила крыла достигает веса самолета и даже превосходит его.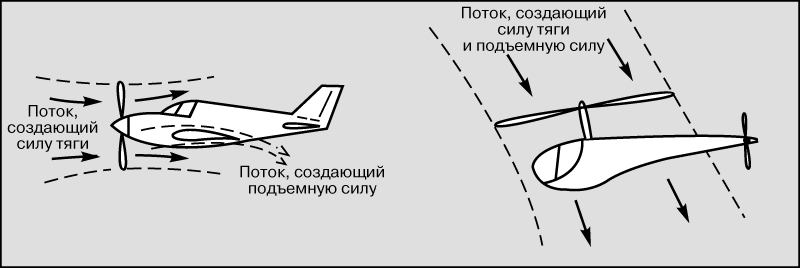 Тогда самолет взлетает. При равномерном прямолинейном полете сумма всех сил, действующих на самолет, равна нулю, как и должно быть согласно первому закону Ньютона. На рис. 1 изображены силы, действующие на самолет при горизонтальном полете с постоянной скоростью. Сила тяги двигателя f равна по модулю и противоположна по направлению силе лобового сопротивления воздуха F2 для всего самолета, а сила
Рис. 1. Силы, действующие на самолет при горизонтальном равномерном полете

тяжести Р равна по модулю и противоположна по направлению подъемной силе F1.

Самолеты, рассчитанные на полет с различной скоростью, имеют различные размеры крыльев. Медленно летящие транспортные самолеты должны иметь большую площадь крыльев, так как при малой скорости подъемная сила, приходящаяся на единицу площади крыла, невелика. Скоростные же самолеты получают достаточную подъемную силу и от крыльев малой площади. Так как подъемная сила крыла уменьшается при уменьшении плотности воздуха, то для полета на большой высоте самолет должен двигаться с большей скоростью, чем вблизи земли. Рис. 2. Судно на подводных крыльях

Подъемная сила возникает и в том случае, когда крыло движется в воде. Это дает возможность строить суда, движущиеся на подводных крыльях. Корпус таких судов во время движения выходит из воды . Это уменьшает сопротивление воды движению судна и позволяет достичь большой скорости хода. Так как плотность воды во много раз больше, чем плотность воздуха, то можно получить достаточную подъемную силу подводного крыла при сравнительно малой его площади и умеренной скорости.

Назначение самолетного винта — это придание самолету большой скорости, при которой крыло создает подъемную силу, уравновешивающую вес самолета. С этой целью винт самолета укрепляют на горизонтальной оси. Существует тип летательных аппаратов тяжелее воздуха, для которого крылья не нужны. Это — вертолеты.

Рис 3. Схема вертолета

В вертолетах ось воздушного винта расположена вертикально и винт создает тягу, направленную вверх, которая и уравновешивает вес вертолета, заменяя подъемную силу крыла.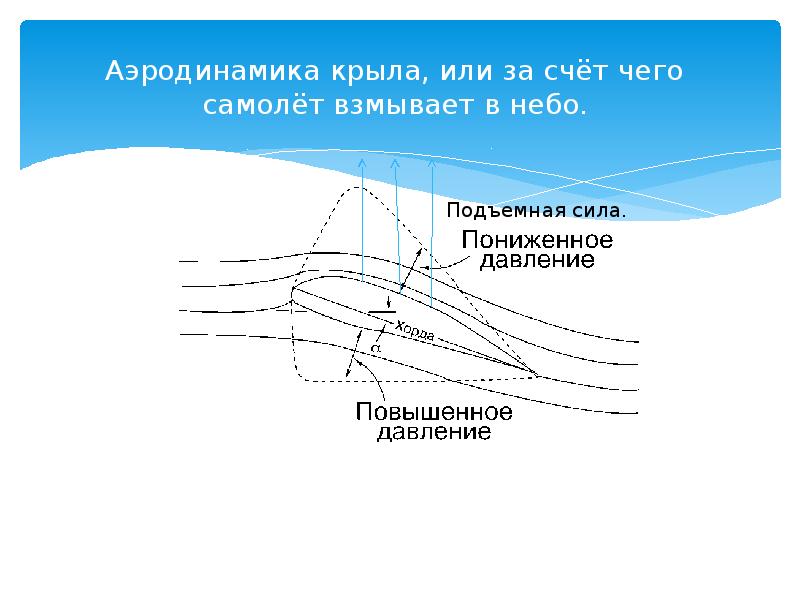 Винт вертолета создает вертикальную тягу независимо от того, движется вертолет или нет. Поэтому при работе воздушных винтов вертолет может неподвижно висеть в воздухе или подниматься по вертикали. Для горизонтального перемещения вертолета необходимо создать тягу, направленную горизонтально. Для этого не нужно устанавливать специальный винт с горизонтальной осью, а достаточно только несколько изменить наклон лопастей вертикального винта, что выполняется при помощи специального механизма во втулке винта.

Литература

1. О.Ф. Кабарлин, В.А. Орлов, А.В. Пономарева, Факультативный курс физики: 8 кл. Учеб. пособиедля учащихся. М: Просвещение. 1985.

Интернет ресурсы

1. Почему и как возникает подъемная сила и лобовое сопротивление

http://flyinghobby.ru/flymodels/

2. Подъемная сила крыла и полет самолета. http://physel.ru/mainmenu-4/eainmenu-15/197-s-192-.html

3. Аэродинамика крыла http://rjstech. com/aerodinamika-i-modelirovanie/osnovy-aerodinamiki/

Архимедова сила. Подъёмная сила — урок. Физика, 7 класс.

На все тела в воздухе, как и в жидкости, действует выталкивающая, или архимедова сила.

Чтобы найти архимедову (выталкивающую) силу, действующую на тело в газе,

надо плотность газа умножить на ускорение свободного падения (\(g=9,8 Н/кг\)) и на объём тела,

находящегося в газе: FА=ρгаза⋅g⋅Vтела.

Обрати внимание!

Для того чтобы летательный аппарат поднялся в воздух, необходимо, чтобы архимедова сила,

действующая на шар, была больше силы тяжести.

На этом основано воздухоплавание.

 

Подъёмная сила воздушного шара зависит от разности архимедовой силы и силы тяжести всей конструкции.

Подъёмная сила увеличивается при увеличении архимедовой силы и уменьшении силы тяжести:
\(F=F_A-F_{тяж}\). 

Плотность газа прямо пропорционально силе тяжести и обратно пропорционально подъёмной силе.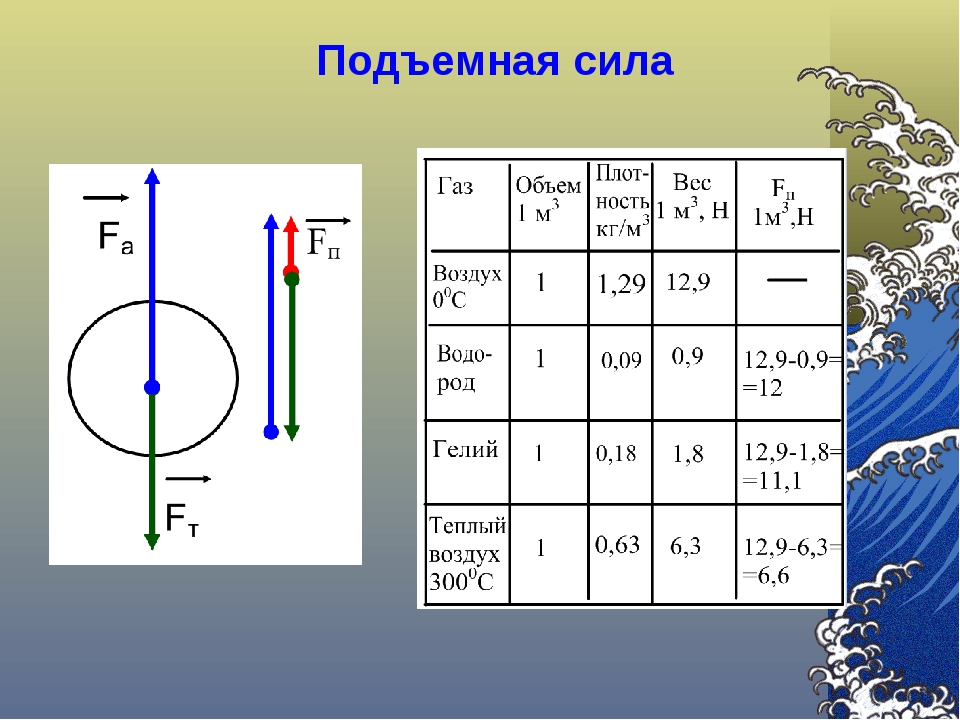

Поэтому для увеличения подъёмной силы нужно использовать газы с малой плотностью (меньшей, чем у воздуха). Одним из таких газов является водород. Однако, водород взрывоопасен, поэтому его для этой цели не используют. Гелий также имеет небольшую плотность, но в отличие от водорода, он не горюч. Это способствует тому, что многие аэростаты заполняют именно гелием.

 

Теплый воздух также имеет меньшую плотность, чем холодный. Поэтому и его можно использовать для создания подъёмной силы.

Чтобы управлять плотностью воздуха, используют газовые горелки. При увеличении пламени газ нагревается сильнее, его плотность уменьшается и шар поднимается выше — подъёмная сила увеличивается. Чтобы снизить высоту воздушного шара, фитиль горелки убавляют, уменьшая скорость нагрева. Воздух внутри шара охлаждается, подъёмная сила уменьшается, шар начинает опускаться вниз.

Таким образом, можно управлять высотой подъёма шара и добиться равенства силы тяжести и силы Архимеда. В этом состоянии шар повисает на одной высоте и будет перемещаться горизонтальными потоками воздуха (ветром).

 

Плотность атмосферного воздуха изменяется с увеличением высоты. Нагревать газ внутри шара можно до определённого значения. Поэтому при равенстве архимедовой силы и силы тяжести подъём аппарата останавливается.

Единственный выход — уменьшить силу тяжести: уменьшить массу груза. Для этого на воздушные шары берут мешки с песком, которые можно выкинуть или отсыпать часть. При уменьшении массы шара уменьшается сила тяжести, что приводит к продолжению подъема аэростата.

Если необходимо опустить на меньшую высоту, уменьшают архимедову силу за счет уменьшения объёма шара. Для этого открывают клапан, и часть газа из шара выходит.

Подъемная сила и сила аэродинамического сопротивления.

Для УДОБСТВА выполнения аэродинамических расчетов полную аэродинамическую силу R можно разложить на три взаимно перпендикулярные составляющие в СКОРОСТНОЙ системе координат. Нетрудно заметить, что при исследованиях ЛА в аэродинамической трубе оси скоростной системы координат фактически «привязаны» к трубе (смотри рис.  14). Составляющую полной аэродинамической силы вдоль оси X назвали силой аэродинамического сопротивления. Составляющую вдоль оси Y — подъемной силой.

Рис. 14. Схема аэродинамической трубы.
1 — воздушный поток. 2 — исследуемое тело.
3 — стенка трубы. 4 — вентилятор.

Где:

R — Полная аэродинамическая сила.

Y — Подъемная сила.

X — Сила лобового сопротивления.

Z — Боковая сила.

Формулы подъемной силы и силы сопротивления очень похожи на формулу полной аэродинамической силы. Что неудивительно, так как и Y, и X являются составными частями R.

Где:

C_y — Коэффициент подъемной силы.

C_x — Коэффициент сопротивления.

r — Плотность воздуха.

V — Скорость тела относительно воздуха (воздушная скорость).

S — Эффективная площадь тела.

В природе не существует самостоятельно действующих подъемной силы и силы лобового сопротивления. Они являются составными частями полной аэродинамической силы.

Говоря о подъемной силе, нельзя не отметить одно интересное обстоятельство: подъемная сила, хотя и называется «подъемной», но она не обязана быть «поднимающей», не обязана быть направлена «вверх». Для того чтобы проиллюстрировать это утверждение, давайте вспомним силы, действующие на безмоторный аппарат в прямолинейном планирующем полете. Разложение R на Y и X строится относительно воздушной скорости ЛА. На рис. 15 видно, что подъемная сила Y относительно земной поверхности направлена не только «вверх», но и немного «вперед» (вдоль проекции траектории полета на землю), а сила сопротивления X не только «назад», но и «вверх».

Рис. 15. Разложение полной аэродинамической силы R
на подъемную силу Y и силу сопротивления X.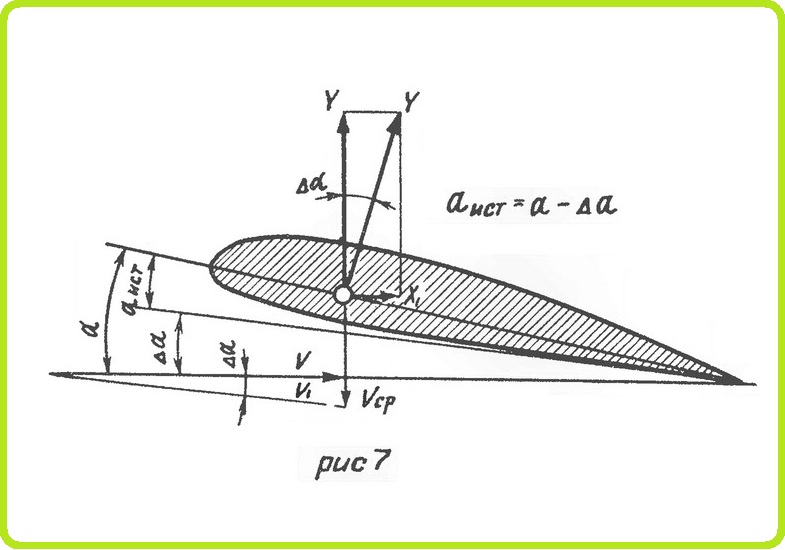

Если же рассмотреть полет круглого парашюта, который фактически не летит, а опускается вертикально вниз, то в этом случае подъемная сила Y (составляющая R перпендикулярная воздушной скорости) равна нулю, а сила сопротивления X совпадает с R (смотри рис. 16).

Рис. 16. У круглого парашюта
подъемная сила равна нулю.

В технике применяют и антикрылья. То есть крылья, которые специально устанавливаются таким образом, чтобы создаваемая ими подъемная сила была направлена вниз. Так, например, гоночный автомобиль прижимается на большой скорости антикрылом к дороге для улучшения сцепления колес с трассой
(смотри рис. 17).

Рис. 17. У автомобиля на антикрыле
подъемная сила направлена вниз.

Источник статьи: http://firstep.ru/kulp/theory/lection-01-02.php

Что такое лифт?

Подъем — это сила, которая прямо противостоит весу самолета и держит самолет в воздухе. Подъемная сила создается каждой частью самолета, но большая часть подъемной силы на обычном авиалайнере создается за счет крылья. Подъемник механический аэродинамическая сила, создаваемая движением самолета в воздухе. Поскольку лифт — это сила, это векторная величина, имеющий как величину, так и направление, связанные с ним.Лифт действует через центр давления объекта и направлена ​​ перпендикулярно направлению потока. Есть несколько факторы которые влияют на величину подъемной силы.

КАК ПОЛУЧАЕТСЯ ЛИФТ?

Есть много объяснений возникновения подъемной силы в энциклопедии, в учебниках по основам физики и на веб-сайтах. К сожалению, многие объяснения вводят в заблуждение и неверны.Теории о создании лифта стали источником великих полемика и тема для жарких споров. Чтобы помочь вам понять рост и его происхождение, мы рассмотрим несколько страниц. описать различные теории и то, как некоторые из популярных теорий неудача.

Подъем происходит при повороте движущегося потока газа. твердым предметом. Поток поворачивается в одну сторону, а подъемник генерируется в обратном направлении, согласно Ньютону Третий закон действия и противодействия.Потому что воздух — это газ и молекулы могут свободно двигаться, любая твердая поверхность может отклонить поток. Для крыла самолета оба верхняя и нижняя поверхности способствуют повороту потока. Пренебрегая часть верхней поверхности при повороте потока приводит к неверная теория лифта.

НЕТ ЖИДКОСТИ, НЕТ ПОДЪЕМНИКА

Подъемник — это механическая сила. Он создается взаимодействием и контакт твердого тела с жидкостью (жидкостью или газом).Нет генерируется силовым полем , в смысле гравитационного поле, или электромагнитное поле , где один объект может воздействовать на другой объект без физического контакта. Для подъема в должно быть создано, твердое тело должно контактировать с жидкостью: нет жидкость, без подъема. Спейс шаттл не остается в космосе, потому что подъемной силы от его крыльев, но из-за орбитальной механики, связанной с его скорость. Космос — это почти вакуум. Без воздуха нет лифта генерируется крыльями.

НЕТ ДВИЖЕНИЯ, НЕТ ПОДЪЕМНИКА

Лифт создается разница в скорости между твердым объект и жидкость. Между объектом и объектом должно быть движение. жидкость: нет движения, нет подъема. Не имеет значения, движется через статическую жидкость, или жидкость проходит мимо статического твердого тела объект. Лифт действует перпендикулярно движению. Тащить, тянуть действует в направлении, противоположном движению.

Вы можете узнать больше о факторы которые влияют на подъемник на этом веб-сайте.Здесь есть много небольших интерактивных программ, которые позволят вам изучить поколение лифта.

Вы можете просмотреть короткий кино из «Орвилла и Уилбура Райтов» обсуждают подъемную силу и как это повлияло на полет их самолета. Файл фильма может можно сохранить на свой компьютер и просмотреть как подкаст на проигрывателе подкастов.

---

Действия:

---

Экскурсии

---

Навигация. .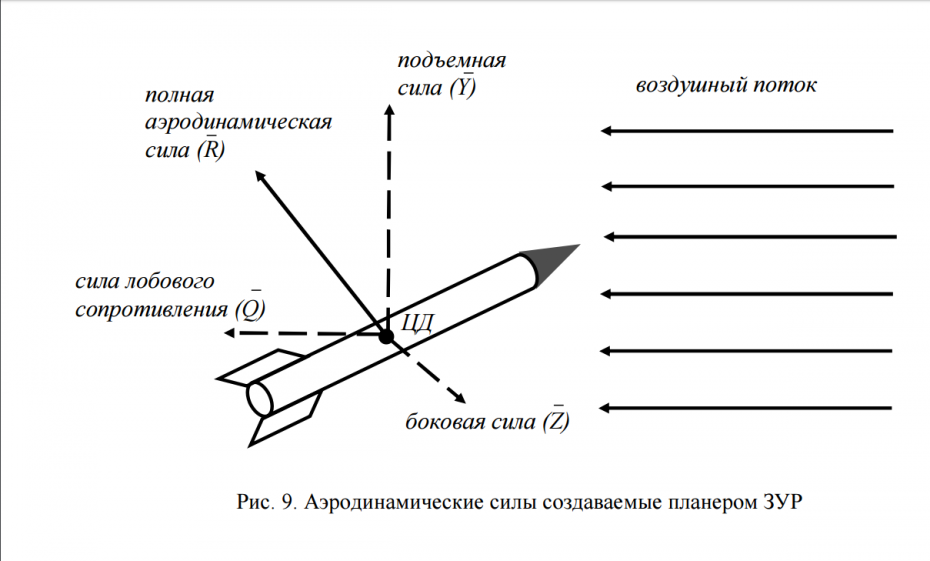

Руководство для начинающих Домашняя страница

Подъем (сила) Факты для детей

Силы на крыле самолета

Подъемная сила , подъемная сила или просто подъемная сила — это сумма всех сил на тело, которые заставляют его двигаться перпендикулярно направлению потока.

Самый распространенный тип подъемной силы — подъемная сила крыла самолета. Но есть много других распространенных применений, таких как пропеллеры на самолетах и ​​лодках, роторы вертолетов, лопасти вентиляторов, паруса на парусных лодках и ветряные турбины.

Хотя обычное значение термина «подъем» предполагает движение «вверх», подъем может быть в любом направлении. Например, для паруса подъемник горизонтальный, а для крыла гоночной машины подъемник опущен.

Есть несколько способов объяснить производство лифта; некоторые из них сложнее других, некоторые оказались ложными. Самое простое объяснение состоит в том, что крыло отклоняет воздух вниз, а реакция толкает крыло вверх.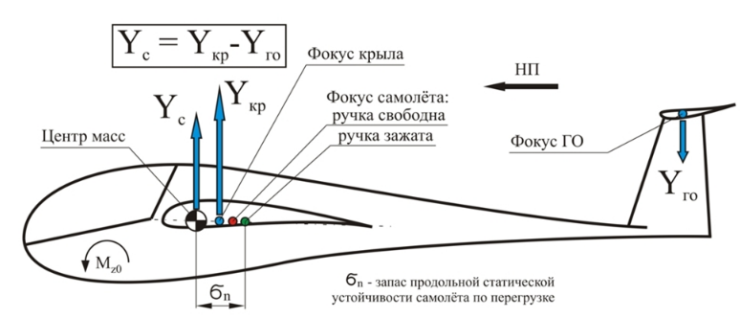

Картинки для детей

• Планер Райт 1902 года демонстрирует свою подъемную силу, поднимаясь вверх

• Обтекание профиля: точки движутся вместе с потоком.Черные точки находятся на временных срезах, которые разделяются на две части — верхнюю и нижнюю — по переднему краю. Заметная разница в скорости между линиями обтекания верхней и нижней поверхности наиболее четко показана на анимации изображения, при этом верхние маркеры достигают задней кромки задолго до нижних. Цвета точек обозначают линии тока.

• Иллюстрация распределения давления выше атмосферного на землю под самолетом в дозвуковом полете

• Поперечное сечение крыла определяет форму крыла.

• Профиль с изгибом по сравнению с симметричным профилем

• Сравнение картины потока без подъема вокруг аэродинамического профиля и картины подъема потока в соответствии с условием Кутта, при котором поток плавно покидает заднюю кромку

• Поперечный разрез крыла и корпуса самолета, показывающий изобары трехмерного подъемного потока

• Расчет Эйлера концевого вихря, скатывающегося из ведомой завихренности

• Вид сверху крыла, показывающий систему подковообразных вихрей

Какая сила используется для подъема груза? — MVOrganizing

Какая сила используется для подъема груза?

гравитация

Выполняется ли работа по поднятию тяжестей?

Поднимая объект, вы работаете с ним. Работа W, совершаемая над объектом постоянной силой, определяется как W = F · d. Он равен величине силы, умноженной на расстояние, на которое объект перемещается в направлении силы.

Как рассчитать подъемную силу тяжестей?

Каждый раз, когда мы поднимаем тяжести, мы прилагаем силу к штанге. В физике мы измеряем силу, используя Второй закон движения Ньютона через уравнение f = ma, или, иначе говоря, сила равна массе, умноженной на ускорение. Чтобы создать больше силы, мы должны либо увеличить массу, либо ускорение (или и то, и другое).

Какое усилие подъемник прилагает для подъема груза?

Расположив точку опоры близко к тяжелому объекту и приложив усилие издалека, можно использовать рычаги для легкого подъема огромных грузов (см. Рисунок 1). Объект, перемещаемый рычагом, часто называют нагрузкой или выходной силой, в то время как сила, приложенная к рычагу, называется усилием или входной силой.

Какие две силы действуют на штангу при подъеме?

Поскольку штанга движется с постоянной скоростью по прямой, результирующая внешняя сила, действующая на нее, должна быть равна нулю. Две внешние силы на штангу точно такие же, как и когда штанга была неподвижной: сила тяжести, действующая вниз, и сила реакции тела, действующая вверх.

Какую роль в силовых тренировках играет гравитация?

Свободные веса (гантели и штанги) добавляют сопротивление упражнениям, тем самым стимулируя ваши мышцы к увеличению силы, размера или выносливости, в зависимости от того, как вы адаптируете упражнения к вашим индивидуальным целям. Поскольку сила тяжести тянет вниз, мышцы, противостоящие этой силе, будут испытывать наибольшую нагрузку.

Как сила тяжести влияет на упражнения?

Влияние силы тяжести на упражнение Гравитация влияет на сокращение мышц, пытаясь притянуть тело или часть тела к полу (если действует против силы тяжести). Например, сгибание живота происходит против силы тяжести, когда верхняя часть тела опускается на пол, что усложняет задачу.

Может ли мышечная сила преодолеть силу тяжести?

Мы прикладываем силу мышц, достаточную для того, чтобы объект не упал обратно на Землю. Мы даже «преодолеваем силу тяжести», стоя или идя, не падая. Во всех этих случаях мы применяем достаточную силу, чтобы противостоять естественной тенденции любого объекта упасть на землю.

Каковы эффекты упражнений с отягощениями?

Увеличение плотности и прочности костей и снижение риска остеопороза. Улучшение самочувствия — тренировки с отягощениями могут повысить вашу уверенность в себе, улучшить образ тела и настроение. Улучшение сна и предотвращение бессонницы. Повышенная самооценка.

Можно ли нарастить мышечную массу с помощью эластичных лент?

Да, вы можете нарастить мышцы с помощью лент с сопротивлением. Все, что вашим мышцам нужно для роста, — это напряжение, адекватное восстановление, адаптация мышц и прогрессирующая перегрузка. Наращивать мышцы можно с помощью упражнений только с собственным весом, поэтому ленты с сопротивлением только увеличат вашу способность к росту мышц.

Ленты сопротивления так же хороши, как и свободные веса?

Когда дело доходит до полос сопротивления против веса, не секрет, что полосы сопротивления намного легче контролировать. Это может быть отличным дополнением к свободным весам, так как вы можете выполнять несколько последних повторений с полосами сопротивления, чтобы безопасно достичь истощения и улучшить диапазон движений!

Подъемная сила и сила сопротивления

Самолеты бросают вызов гравитации. Гоночные автомобили Формулы 1 поворачивают на невероятных скоростях, создавая поперечные силы в 4,5 раза больше силы тяжести. Яхты могут обогнуть земной шар только с помощью энергии ветра. Все эти невероятные достижения связаны с подъемной силой, создаваемой аэродинамическими профилями, движущимися в воздухе.Конечно, ничего не дается бесплатно; Стоимость подъемника указана.

Доступные расчеты подъемной силы и сопротивления уже доступны

Готовы ли вы к 30-дневной бесплатной пробной версии Caedium Professional?

Подъемник

Подъемная сила или прижимная сила, известная в мире автоспорта, — это сила, создаваемая перпендикулярно направлению движения объекта, движущегося в жидкости (газе или жидкости). Тот же эффект возникает, когда жидкость движется над неподвижным объектом, например над аэродинамической трубой.Аэродинамические поверхности являются наиболее эффективными формами, найденными на сегодняшний день, которые могут создавать подъемную силу и в то же время минимизировать сопротивление.

Перетащите

Перетаскивание — это неизбежное следствие движения объекта в жидкости. Сопротивление — это сила, генерируемая параллельно и противоположно направлению движения объекта, движущегося в жидкости. Перетаскивание можно разбить на следующие два компонента:

• Сопротивление формы (или сопротивление давлению) — зависит от формы объекта, движущегося в жидкости
• Трение кожи — зависит от вязкого трения между движущейся поверхностью и жидкостью, полученного из напряжения сдвига стенки

Сопротивление формы для трехмерного крыла также включает индуцированное сопротивление, которое создается на концах крыла, когда воздух под высоким давлением с нижней поверхности крыла приводится в движение благоприятным градиентом давления (от высокого к низкому) вокруг воздуха с низким давлением.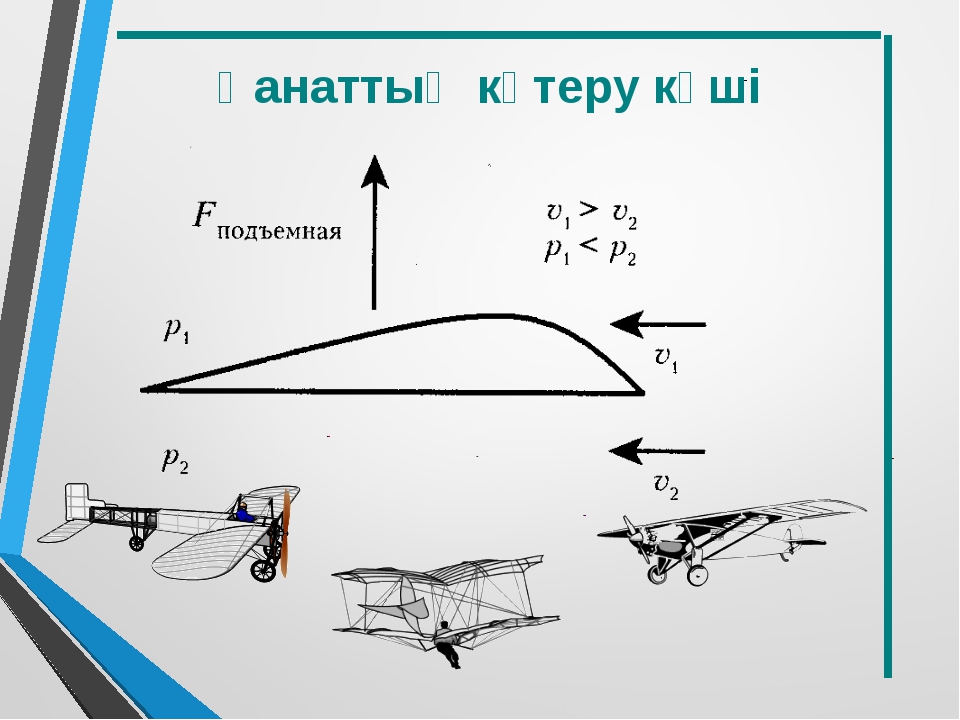 на верхней поверхности, образуя концевые вихри.

Вихрь на кончике крыла, видимый в следе для расчета панельным методом

Эти вихри иногда видны как следы водяного пара во влажные дни, особенно в условиях большой подъемной силы, когда лайнеры взлетают и приземляются. Торцевые пластины на крыльях гоночных автомобилей и винглеты на самолетах помогают уменьшить силу завихрений на концах крыльев и, таким образом, уменьшить индуцированное сопротивление.

Коэффициенты подъема и сопротивления

Подъемная сила и сопротивление изменяются в зависимости от угла, под которым аэродинамический профиль определяется направлением его движения в жидкости.Этот угол известен как угол атаки, угол падения или альфа. При оценке профиля обычно выполняют альфа-развертку, которая регистрирует подъемную силу и сопротивление профиля под разными углами. Подъемная сила и сопротивление обычно изображаются как безразмерные величины.

Сравнение коэффициента подъемной силы между расчетом и экспериментом

Безразмерный коэффициент подъемной силы и коэффициент лобового сопротивления определяются как:

L = C _L . А. q _инф
D = C _D . А. q _инф

где:
L — подъемная сила
C _L — безразмерный коэффициент подъемной силы
D — сила сопротивления
C _D — безразмерное сопротивление коэффициент
A — эталонная площадь, обычно площадь в плане (максимальная площадь проекции на плоскость) профиля или крыла
q _inf — динамическое давление жидкости в набегающем потоке из уравнения Бернулли:

q _inf = 1/2 rho _inf .V _инф ²

где:
rho _inf — плотность жидкости в набегающем потоке
V _inf — скорость жидкости в набегающем потоке

Площадь плана используется для расчета коэффициента лобового сопротивления только для профилей. Для всех других форм, таких как автомобили, эталонная область — это фронтальная область формы, спроецированная на плоскость, перпендикулярную направлению потока.

Численный расчет полной силы

Подъемная сила и сила сопротивления в эксперименте в аэродинамической трубе измеряются непосредственно с помощью весов.Для численных методов, которые создают силы в дискретных точках сетки, общая сила получается путем суммирования сил на всех элементах сетки. Сила, действующая на отдельный элемент сетки, определяется как:

F _i = (p _i . N _i + tau _i ). А _и

где:
p _i — давление в центре элемента
tau _i — напряжение сдвига стенки в центре элемента
A _i — область элемента
n _i — направление нормали элемента
i — i-й элемент

Предполагая, что поток выровнен по направлению z, общая сила разделена на составляющие подъемной силы и силы сопротивления как:

L = F _y . cos (альфа) — F _x . sin (альфа)
D = F _x . cos (альфа) + F _y . грех (альфа)

где:
L — подъемная сила
D — сила сопротивления
F _x — сила в направлении x
F _y — сила в направлении y
alpha — угол атаки

Aerodynamic Lift — обзор

10.5.1 Подъемная сила

Как и многие другие аэродинамические явления, аэродинамические силы пантографа изменяются в квадрате относительной скорости ветра, действующей на пантограф, как показано для аэродинамической подъемной силы на рис. 10.11. Давно известно, что для большинства конструкций пантографов большая часть подъемной силы создается головкой пантографа (Peacock, 1967). Пимпуткар (1971) предполагает, основываясь на предыдущих исследованиях, проведенных во Франции, России и Великобритании, что 80% аэродинамической подъемной силы создается головой, и только 20% исходит от рамы.

Рисунок 10.11. Вариант аэродинамического подъёма однорычажного пантографа Schunk с относительной скоростью ветра.

Данные Carnevale et al. (2017). Авторское право Elsevier.

Идеальный пантограф будет иметь аэродинамический подъем, который будет нейтральным при увеличении скорости поезда, а также в каждом направлении движения, если пантограф асимметричный, как и пантограф с одной рукой. Исторически сложилось так, что было проведено большое количество исследований и измерений аэродинамической подъемной силы и влияния различных конструкций компонентов пантографа на подъемную силу.Одним из усложняющих факторов является то, что кажущиеся незначительными изменения конструкции могут существенно повлиять на подъемную силу. Например, на рис. 10.12 показана работа, проведенная во Франции в 1950-х годах и описанная в Pimputkar (1971), по влиянию конструктивных изменений держателей углеродных полос (показаны в поперечном сечении справа) на подъемную силу пантографа.

Рисунок 10.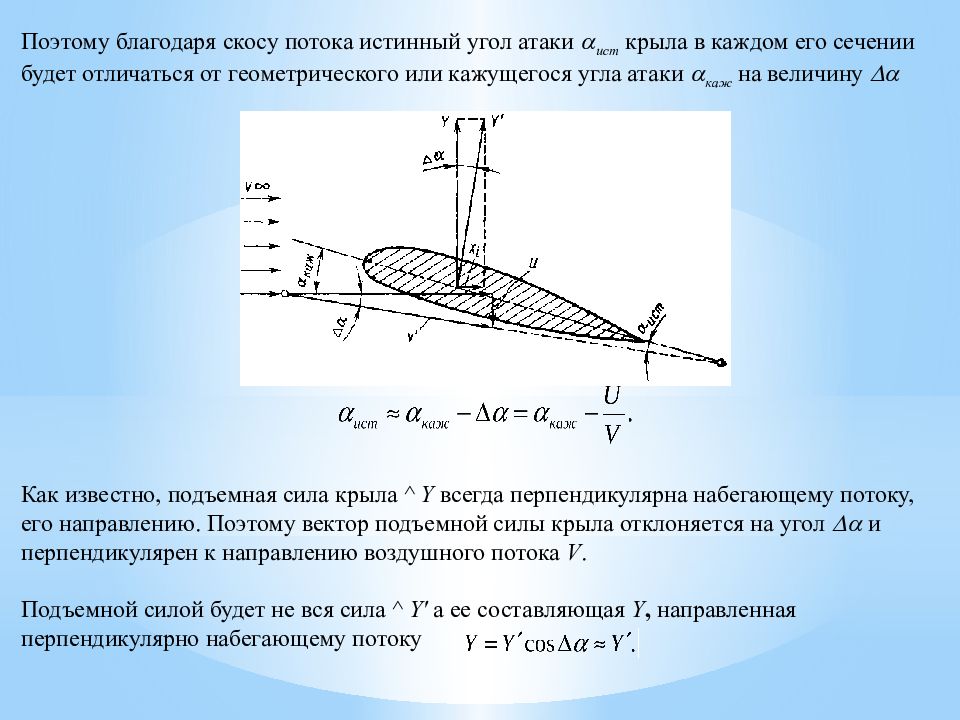 12. Относительное увеличение подъема пантографа для различных конструкций держателей углерода.

Данные из Пимпуткара (1971).

Другими аспектами, вызывающими озабоченность при рассмотрении подъемной силы пантографа, являются эффекты переменного угла рыскания, поскольку, очевидно, естественный ветер может действовать под любым углом к ​​направлению пути, а также угол крена ветра, действующий на пантографы, что может происходить как в результате движения вагонов с пантографами поездов по наклонным путям и угловатости потока из-за крутых высоких насыпей.Последним вопросом, который влияет на подъемную силу, является высота пантографа (поскольку составные части пантографа будут находиться под разными углами к начавшемуся относительному ветру), но этот вопрос подробно не изучался. Тем не менее, см. Coxon (1981) для подробностей некоторых натурных испытаний и Harrison (1988) для описания испытаний в аэродинамической трубе, исследующих этот аспект.

На рис. 10.13 показаны измерения в аэродинамической трубе изменения коэффициента аэродинамической подъемной силы (на основе площади 10 м ² ) для результирующей воздушной скорости 30 м / с для однорычажного пантографа AMBR Faiveley, как сообщает Rigby. и Gawthorpe (1979).Измерения были выполнены для всего диапазона углов рыскания, при этом угол 0 градусов представляет поток вдоль продольной оси поезда с ведущим кулаком пантографа, а 180 градусов представляют поток вдоль продольной оси поезда с ведомым кулаком пантографа. Также были протестированы два угла крена: 0 градусов соответствует горизонтальному результирующему ветру, действующему на пантограф, и 25 градусов — экстремальному сочетанию наклонной дорожки и крутой насыпи. Можно отметить, что поведение подъемной силы совершенно различается в направлениях движения вперед и назад кулака, и что угол крена имеет сильное влияние, увеличивая значения подъемной силы.

Рисунок 10.13. Вариации коэффициента подъемной силы для одного пантографа AMBR при углах крена 0 и 25 градусов.

Данные Ригби и Гоуторпа (1979).

На рис. 10.14 показано изменение аэродинамической подъемной силы для пантографа AMBR как в переднем, так и в заднем направлениях кулака в зависимости от скорости поезда без бокового ветра. Хотя подъемы относительно небольшие, все же существует разница в подъеме в зависимости от направления пантографа, и можно видеть, что поведение сильно отличается от поведения пантографа Шунка, показанного на рис.10.11.

Рисунок 10.14. Изменение аэродинамической подъемной силы для пантографа AMBR.

Эти асимметрии в поведении аэродинамической подъемной силы, зависящие от направления движения пантографа и увеличивающиеся с увеличением скорости поезда и бокового ветра, привели к поиску того, какие компоненты пантографов влияют на подъемную силу и как, как показано на рис. 10.12, в частности, поиск, чтобы исправить асимметрию направленного подъема.

Во время разработки высокоскоростного пантографа British Rail / Brecknell-Willis в 1970-х и 1980-х годах была проделана большая работа по преодолению асимметричных аэродинамических характеристик подъемной силы.Коксон (1981) описывает хронологию развития этого пантографа и проведенных испытаний. Особый интерес вызывало использование аэродинамических крыльев, прикрепленных к апексной раме, чтобы попытаться уравновесить значения аэродинамической подъемной силы в каждом направлении движения. Эти крылья до сих пор используются на пантографах Brecknell-Willis, как можно увидеть на рис. 10.15, где показан пантограф, установленный на класс 390. Для повышения их эффективности они оснащены концевыми пластинами, которые можно увидеть на рис. 10.15. А.

Рисунок 10.15. Виды пантографа класса 390 с аэродинамическими крыльями на вершине рамы.

(A) Вид спереди; (B) установлен на класс 390.

Используется с разрешения Brecknell-Willis.

Другие подходы, используемые для улучшения подъемных характеристик пантографа British Rail / Brecknell-Willis с использованием испытаний в аэродинамической трубе, описаны в Harrison (1988). Геометрические изменения включали обтекание различных частей рамы пантографа, изменение головки пантографа путем изменения расстояния между угольными полосами, изменение количества установленных угольных полос и заполнение пространства между полосами.Ожидалось, что эти изменения изменят аэродинамические характеристики пантографа, хотя было понятно, что некоторые из них не могут быть применены к служебному пантографу. Действительно, некоторые изменения ухудшили показатели подъема, но, тем не менее, указали на важные тенденции. Также была предпринята попытка улучшить характеристики пантографа, работающего на максимальной высоте троса, путем установки вспомогательного аэродинамического профиля, прикрепленного к верхнему рычагу пантографа. В целом, ни одна из модификаций не дала значительных улучшений подъемной силы во всем диапазоне возможных условий эксплуатации, хотя использование обтекателей и вспомогательного аэродинамического профиля показало некоторые перспективы.На рис. 10.16 показан пример влияния модификаций компонентов на аэродинамический подъем. (Горизонтальные линии показывают подъем в переднем и заднем положениях сустава для немодифицированного пантографа.)

Рис. 10.16. Влияние модификации элементов пантографа на аэродинамическую подъемную силу.

Данные Харрисона (1988).

Использование аэродинамических крыльев для регулировки характеристик асимметричной подъемной силы пантографа, однако, приводит к трудностям в обеспечении оптимального выбора угла аэродинамического профиля.Харрисон и Ригби (1990) описывают натурные испытания, проведенные на локомотивах классов 89, 90 и 91 (см. Рис. 10.9), с использованием метода привязной головки для измерения аэродинамической подъемной силы. Все локомотивы могли приводить в движение поезда с ведущим или ведомым кулаком пантографа. Класс 89 работал только в режиме буксировки, в то время как два других локомотива работали в режимах тяги и движения. Кроме того, у Class 91 обтекаемый и резкий конец. Для этого была проведена сложная серия испытаний, включающих настройку крыльев на 5, 10 и 15 градусов и испытания во всех возможных режимах работы.Можно видеть, что воздушный поток, приближающийся к пантографам во всех различных режимах, может быть изменен длиной цепи и вырезом пантографа выше по потоку. Результаты показали, что компромиссные оптимальные углы аэродинамического профиля составляли около 10, 8 и 10 градусов для локомотивов классов 89, 90 и 91 соответственно. При определенных комбинациях условий эксплуатации для этих вариантов могут быть превышены пределы подъема, и ни одна характеристика подъема не была нейтральной для поезда.

Другой подход к исправлению асимметрии подъемной силы однорычажных пантографов был использован компанией Central Japan Railway Company при разработке поезда серии N700 Shinkansen, см. Nakamura et al.(2011). Серьезной проблемой для высокоскоростных японских поездов является аэроакустический шум, одним из значительных источников которого были пантографы. Предлагаемая шумоподавляющая конструкция пантографа N700, основанная на пантографе серии 700, включала обтекатель над нижним рычагом пантографа. Отдельный вклад головки пантографа, а также нижнего и верхнего рычагов пантографа был определен путем тестирования в аэродинамической трубе оригинального пантографа серии 700 и пантографа N700. Это показало, что подъемные силы на плечах пантографа серии 700 в целом компенсируют друг друга, оставляя только подъемную силу на головке.(Подъемные силы в корпусах ведущего и ведомого кулаков не были ни незначительными, ни равными, но предположительно находились в допустимых пределах.) Однако обтекатель нижнего рычага на пантографе N700 привел к значительному увеличению асимметрии подъемной силы в двух направлениях движения. Использование крыла на голове было исключено, так как это увеличило бы аэроакустический шум пантографа. Предлагаемое решение заключалось в увеличении угла наклона головки, что создавало силу сопротивления на голове с дополнительной составляющей подъемной силы.

В целом эти исследования подъемной силы проводились в аэродинамических трубах или полномасштабных испытаниях, но в последнее время все чаще используются исследования CFD. Carnevale et al. (2016) и Carnevale et al. (2017) использовали CFD для исследования общего подъема пантографа и вкладов в подъем различных компонентов пантографа. Используя измерения подъема в аэродинамической трубе с помощью полномасштабного однорычажного пантографа Schunk, того же пантографа с ветрозащитным экраном вверх по потоку и пантографа с инструментальной головкой, они подтвердили свою модель CFD в направлениях переднего и заднего суставов.Используемый метод представлял собой RANS-моделирование с моделью k-ω SST для турбулентности, и область была разделена на 20 миллионов ячеек. Согласие между измерениями в аэродинамической трубе и прогнозами CFD в целом было превосходным. Полная модель CFD с использованием 40 миллионов ячеек была использована для сравнения с натурными трековыми измерениями подъема инструментального пантографа с головкой. Сравнение результатов измерений и прогнозов показало, что CFD работает хорошо. Наблюдались некоторые заметные различия между результатами в аэродинамической трубе и результатами испытаний рельсовых путей в поведении подъема в направлении поворота кулака, которое было приписано развитию пограничного слоя поезда и эффектам выемок на крыше выше по потоку.

Zhang et al. (2017) также использовали CFD для моделирования подъема на пантографах CX-PG модели поезда из восьми вагонов длиной 200 м в полном масштабе. Область состояла из 33 миллионов ячеек, и они также использовали моделирование RANS с моделью турбулентности k-ω SST. Моделирование проводилось для направления движения кулака вперед и назад с пантографом спереди и сзади второго и седьмого вагонов поезда. Неудивительно, что подъем пантографа значительно выше, когда пантограф находится ближе всего к передней части поезда.

При указании требуемых подъемных характеристик пантографов может показаться целесообразным рассмотреть возможность использования максимальной скорости поезда в сочетании с некоторым допуском для конкретной скорости встречного ветра. Однако, когда поезда входят в туннели, может возникнуть значительный обратный поток воздуха из туннеля к входному порталу из-за вытеснения воздуха поездом. Таким образом, вход поезда в туннель с высоким коэффициентом блокировки может быть наиболее подходящим сценарием для определения максимальной относительной скорости воздуха вдоль поезда.Хотя высокие подъемы могут быть вызваны боковым ветром, они обычно не учитываются в спецификациях пантографа. В будущем такие сценарии следует рассматривать в рамках оценки рисков, чтобы гарантировать, что высокие подъемы не произойдут с неприемлемой вероятностью.

(PDF) Подъемная сила крыла самолета при горизонтальном полете на высоких скоростях. Объяснение вихревого следа.

под аэродинамическим профилем, что объясняет подъемную силу крыла самолета, показанную на рис.1. Однако,

нет свидетельств того, что воздушная скорость выше крыла самолета. Как оказалось, этой проблеме

более ста лет.

Если посмотреть на движение воздуха вокруг профиля в горизонтальном полете, не обращая внимания на надписи на рис.1

, становится очевидным, что скорость воздуха над крылом самолета

меньше воздушной. скорость под крылом самолета.

Действительно, рисунок 1 ясно показывает, что крыло самолета отбивает воздух от верхней части профиля

, как холм в открытом поле.Очевидно, что ветер за холмом меньше, поэтому скорость воздуха

над профилем меньше, чем под профилем в горизонтальном полете. Так устроены все крылья самолета

, у них есть утолщение перед крылом над линией горизонта.

Вдобавок воздух действительно давит на крыло самолета сверху, исходя из конструкции крыла

, так как касательная к крылу имеет острый угол с горизонтом, а снизу

воздух проходит параллельно с горизонтом. крыло и не оказывает дополнительного давления (рис.1). Острый угол

между касательной к профилю и линией горизонта в верхней части аэродинамического профиля фактически означает

, что профиль крыла самолета создает угол атаки сверху для встречного воздушного потока,

, когда крыло горизонтальное (с нулевым углом атаки под крылом самолета).

Как известно [2-4], при выводе подъемной силы Жуковский использовал тот факт, что скорость воздушного потока больше над крылом

самолета (рис.1). Следовательно, он получил подъемную силу.

Однако, если учесть реальную ситуацию, когда скорость воздушного потока под крылом на

больше скорости над крылом самолета в горизонтальном полете, то сила Жуковского

направлена ​​вниз вместе с давление воздуха, которое давит на крыло самолета

сверху.

Действительно, аналогия между крыловым профилем с вращающимся цилиндром в набегающем потоке воздуха, которую использовал

Жуковский, не выдерживает критики.Во-первых, симметричный цилиндр не эквивалентен

асимметричному аэродинамическому профилю, поэтому они будут вести себя по-разному при набегающем воздушном потоке.

Во-вторых, даже если предположить, что в их поведении есть некоторая корреляция, асимметричный профиль

при нулевом угле атаки замедляет набегающий воздушный поток от верхней части крыла самолета

, поскольку создает барьер для поток воздуха сверху. Следовательно, асимметричный профиль при нулевом угле атаки

будет соответствовать цилиндру, вращающемуся против часовой стрелки в набегающем потоке, так что

, чтобы скорость воздуха в верхней части цилиндра была меньше.Как известно [4], на такой вращающийся цилиндр в набегающем потоке будет действовать направленная вниз сила

.

Вязкость в воздухе низкая, это явно не поможет удержать самолет в воздухе. Однако

Прандтль учитывал вязкость воздуха в пограничном слое при описании подъемной силы

самолета [4]. Но он также предположил, что скорость воздуха над профилем больше (рис. 1), поскольку

сила вязкости зависит от скорости.Следовательно, если теперь пересчитать силы

, полученные Прандтлем, они также будут направлены вниз.

Таким образом, принцип вязкости и подобия, который используется при описании движения вязкой жидкости

[4], не поможет нам объяснить подъемную силу самолета. Профиль

задает градиент давления и градиент скорости по вертикальной оси. Следовательно, если Жуковский и Прандтль получили

восходящих сил на основе распределения (рис.1), то теперь при пересчете, учитывая, что скорость воздуха

больше под крылом самолета, а давление воздуха над крылом

самолета больше, эти силы будут направлены вниз.

Подъемная сила стального клина и несущего болта

Стальной клин — чрезвычайно важный аспект любого строительного процесса. Еще один способ понять силу стального клина — это понять конструктивный болт. Сначала может показаться, что у этих двух продуктов нет ничего общего, но на самом деле это одно и то же.

И клин, и винт — простые машины, основанные на принципе наклона. Фундаментальная теория состоит в том, что для перемещения объекта вверх по склону требуется меньше энергии, чем для того, чтобы поднять его прямо сверху. В то время как стальной клин работает по прямой линии, структурный болт делает то же самое, только по спиральной линии. Оба они по-прежнему считаются клиньями или «наклонами», в зависимости от вашего предпочтительного термина.

При вычислении силы расширения, «подъема» (клин) или сжатия (структурный болт) уравнение одинаково.Длина наклона, разделенная на расстояние подъема.

В случае рисунка 1, изображенного выше, подъемную силу 12,40 можно рассматривать в процентах. Чтобы поднять объект прямо вверх, требуется сила, равная 100% веса объекта. Чтобы поднять тот же объект с помощью стального клина, требуется всего 12,40% этой силы.

Если связать то же уравнение с конструкционным болтом, то наклон остается прежним. Он измеряется как расстояние между двумя нитями.Длина теперь измеряется как окружность ствола затвора. Обратите внимание, что на рис. 2 выше показано, что это можно измерить от внешнего края резьбы, от внутреннего или от середины резьбы. Кроме того, все три диаметра меньше фактического диаметра. То есть болт диаметром 1 дюйм имеет большой диаметр 0,9980 дюйма, делительный диаметр 0,9134 дюйма и вспомогательный диаметр 0,8446 дюйма. Чтобы не усложнять это объяснение, мы использовали 1 дюйм в качестве диаметра.

Окружность круга диаметром 1 дюйм равна 3.14 ”. Согласно спецификациям болтов UNC, у болта диаметром 1 дюйм имеется 8 витков резьбы на дюйм, поэтому каждая резьба поднимается на расстояние 1/8 дюйма. На рисунке 3 выше показано, как болт на самом деле представляет собой клин. При этом новая переменная — длина. Однако, поскольку длина равна окружности, теперь она составляет 3,14 дюйма.

1/8 ÷ 3,14 = 0,0398

Здесь следует напомнить, что результат 0,0398 фактически можно рассматривать как процент, а для простоты число можно округлить до 4 процентов.Это означает, что для создания 100 процентов силы требуется всего 4 процента давления.

До сих пор упоминалось только клиновое действие болта. Рычаг, создаваемый рукояткой гаечного ключа, затягивающей болт, только усиливает это давление.

На Рисунке 4 выше мы видим, что стандартная шестигранная головка для болта диаметром 1 дюйм составляет 1-1 / 2 дюйма от плоского до плоского. Поскольку точкой поворота является центр или ось, расстояние до любого плоского края составляет 3/4 дюйма. Соотношение 24-дюймовой ручки составляет 1:32.Таким образом, показанный выше процент в 4 процента, или 25-кратное преимущество, теперь снова умножается на 32. Полное преимущество, создаваемое этим клином и рычагом, составляет 800-кратное фактическое прикладываемое давление. С этими результатами легко увидеть, как наклон стального клина или конструкционного болта все упрощает.

Чтобы увидеть конкретные виды стальных клиньев, которые мы предлагаем, щелкните ниже!

.