Система координат ортодромическая: Геонавигационная информация/ Навигационные системы координат

Системы координат, применяемые в самолетовождении

Форма Земли. Фигура Земли по форме близка к эллипсоиду вращения малого сжатия, который образуется вращением эллипса вокруг его малой оси. Большая полуось земного эллипсоида, или радиус экватора, составляет 6378,245 км, малая —6356,836 км.

Все авиационные карты, траектории полета самолетов, ракет и других летательных аппаратов, составляются и рассчитываются с учетом сжатия Земли. Однако многие практические задачи самолетовождения решаются в предложении, что Земля по форме является шаром со средним радиусом R = 6371 км.

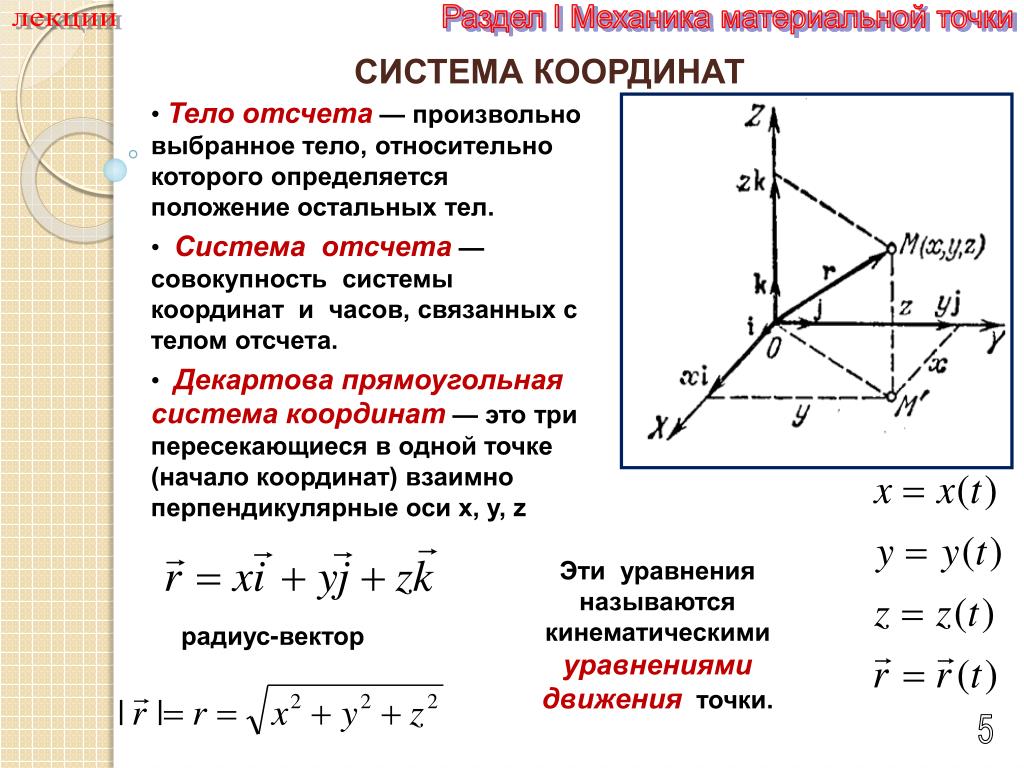
Положение места самолета, т. е. проекция его центра масс на поверхность Земли, может определяться в географической, сферической, ортодромической, прямоугольной и полярной системах координат.

Географическая система координат.

Положение места самолета на поверхности эллипсоида Земли в географической системе координат определяется географической широтой φ и географической долготой λ (рис. 1).

Рисунок 1

Для построения географической системы координат земной эллипсоид пересекается плоскостями, перпендикулярными оси вращения Земли, и плоскостями, проходящими через ось вращения Земли.

Линии пересечения плоскостей, перпендикулярных оси вращения Земли, с земной поверхностью представляют собой параллельные окружности. Плоскость, проходящая через центр Земли, пересекает ее поверхность по окружности, называемой земным экватором. Линии пересечения поверхности Земли другими параллельными плоскостями называются параллелям и.

Плоскости, проходящие через ось вращения Земли, пересекают ее поверхность по окружностям, называемым меридианами. За начальный принимается меридиан, проходящий через Гринвичскую обсерваторию вблизи Лондона.

Географической широтой φ называется угол между плоскостью экватора и направлением нормали земного эллипсоида в данной точке. Широта измеряется от плоскости экватора к полюсам в пределах 0—90°. Северная широта считается положительной, южная — отрицательной.

Географической долготой λ называется двугранный угол между плоскостью Гринвичского меридиана плоскостью меридиана данной точки. Долгота измеряется к востоку и к западу от начального меридиана от 0 до 180°. Долгота к востоку от начального меридиана называется восточной и считается положительной. Долгота к западу от начального меридиана называется западной и считается отрицательной. Долгота может также измеряться в единицах времени: часах, минутах и секундах.

Для решения многих задач пилотирования и самолетовождения требуется определять направление вертикали в точке места самолета. За направление вертикали принимается направление, по которому устанавливается 1лечо маятника или нить отвеса.

Если считать фигуру Земли сферой, то вертикаль является продолжением радиуса Земли, проведенного в данную точку.

Плоскость, перпендикулярная направлению вертикали и касательная в какой-либо точке М к земной поверхности, называется плоскостью горизонта этой точки. Плоскость горизонта пересекается с плоскостями меридиана и параллели места по прямым NS и EW. Прямая NS указывает направление север — юг, прямая EW — направление восток — запад. Прямая NS называется полуденной линией.

В сферической системе координат положение точки па поверхности земной сферы определяется сферической широтой и сферической долготой

с. Сферическая широта измеряется углом между плоскостью экватора и направлением на данную точку из центра земной сферы. Сферическая долгота измеряется двугранным углом между плоскостью начального меридиана и плоскостью меридиана данной точки, т. е.

определяется тем же углом, что и географическая долгота, Ортодромическая система координат является разновидностью сферической системы координат. За координатные оси ортодромической системы принимаются две взаимно перпендикулярные дуги окружностей больших кругов на поверхности Земли. Одна окружность образуется большим кругом, проходящим через начальную М_си конечную М_к точки (рис.2). Дуга большого круга, соединяющая эти две точки, называется ортодромией. Ортодромия представляет собой кратчайшее расстояние между точками, измеренное по поверхности шара.

Ортодромическая система координат используется в пределах сферического пояса, ограниченного двумя малыми кругами а и б, параллельными ортодромии и симметрично расположенными относительно нее. Положение ортодромии на земной поверхности может быть определено, если задано положение одного из двух его полюсов Р или Р’.

Рисунок 2

Полюсами большого круга называются две точки на поверхности шара, которые расположены на противоположных концах его диаметра, перпендикулярного плоскости большого круга.

В качестве координат точки в ортодромической системе принимаются боковое уклонение от ортодромии и дальность по ортодромии.

Боковым уклонением от ортодромии Х₀щ называется дуга ортодромического меридиана между ортодромией (точка

т) и заданной точкой М. Эта дуга соответствует углу МОт между радиусами Земли ОМ. и От. Отсчет бокового уклонения со знаком плюс производится вправо от ортодромии, т. е. в направлении к правому полюсу, и со знаком минус — влево.

Дальностью по ортодромии У₀рт называется дуга М₀т между начальной точкой ортодромии М₀ и точкой т, расположенной на ортодромическом меридиане. Эта дуга соответствует углу МцОт между радиусами Земли ОМ₀и От. Отсчет дальности производится от начальной М₀или от конечной М_к точек до точки т. Ортодромические координаты аналогичны географическим: боковое уклонение— это широта, дальность по ортодромии — долгота.

Для указания места, в котором находится самолет над поверхностью Земли, и определения направления его движения в самолетовождении пользуются понятиями о точке местонахождения самолета и его курсе.

Точкой местонахождения (или точкой места самолета) называется точка земной поверхности, на вертикали к которой в данный момент времени находится центр масс самолета. При движении самолета точка его места описывает на земной поверхности некоторую кривую, называемую линией пути. Географические или орто-дромические координаты точки местонахождения самолета в данный момент времени называются его текущими координатами.

Если провести через центр масс самолета О (рис. 3) вертикальную линию ZO и продолжить ее вниз до пересечения с земной поверхностью, получим точку М местонахождения самолета.

Рисунок 3

Плоскость Я, перпендикулярная вертикали и проходящая через точку М, представляет собой плоскость горизонта этой точки. На ней можно показать горизонтальную проекцию продольной оси самолета х\х\, которая пройдет через точку места М. Направление линии х\х( на плоскости горизонта определяется углом, который она образует с некоторым постоянным направлением, выбранным за начало отсчета углов. Этот угол называется курсом самолета.

В географической системе координат углы в плоскости горизонта отсчитываются от северного направления меридиана — линии NS до положительного направления проекций оси самолета х\х\. Курс, отсчитанный таким образом в географической системе координат, называется истинным и обозначается ИК. В ортодромической системе координат (рис. 2) за основное направление принято положительное направление ортодромической параллели (линии Mq

). Курс, отсчитанный от этого направления, называется ортодромическим и обозначается ОК.

Во всех системах координат курс отсчитывается от основного направления вправо по часовой стрелке от 0 до 360°.

Рисунок 4

Для определения соотношения между истинным и ортодромическим курсами рассмотрим рис. 4, на котором обозначены: М — точка места самолета, дуга MP_N —северное направление географического меридиана, МР₀— ортодромический меридиан, q‘q — дуга ортодромической параллели, х’_гх’_г — проекция продольной оси самолета на плоскость горизонта, — β путевой угол ортодромии, т. е. угол между северным направлением.

Ортодромическая система координат.

Ортодромическая системы является обобщающим случаем сферических координат. Вместо «настоящих» меридианов и параллелей, как в географических системах, используются меридианы и параллели условные, наиболее удобно расположенные относительно маршрута полета.

В ортодромических системах осями являются две ортодромии, перпендикулярные друг другу в начале системы координат. В зависимости от того, как направлены эти оси и где расположено начало системы координат, различают две их группы.

а) Главноортодромические.

Начало обычно размещается в ИПМ, а одну из осей, называемую главной ортодромией, направляют вдоль маршрута. Например, так, чтобы она проходила и через КПМ, либо вблизи всех ППМ. Главная ортодромия является экватором такой условной сферической системы координат. Вторая ось направляется вправо от направления полета.

Координаты могут быть выражены как в линейной мере (в километрах), так и в угловой мере, аналогично широте и долготе

Рис. 23.4 Главноортодромическая система координат.

Преимущество главноортодромической системы состоит в том, что она используется одна на весь маршрут. Можно заранее рассчитать в этой системе координаты ППМ и близко расположенных радиомаяков, определять МС. Недостаток же ее заключается в том, что по значениям координат, например X и У, невозможно судить непосредственно о расположении ВС относительно ЛЗП. Даже при точном следовании по маршруту обе координаты будут изменяться, поскольку маршрут имеет изломы и участки маршрута, как правило, не совпадают ни с одной из осей. Вместе с тем, такие системы координат применяются в пилотажно-навигационных комплексах некоторых типов ВС. Система координат такого типа может использоваться и при внемаршрутных полетах, когда полеты выполняются в ограниченном район, например, при выполнении авиационных работ. В этом случае начало системы координат располагают в одной из точек этого района (например, на аэродроме вылета), а оси направляют по меридиану и перпендикулярно к нему (по касательной к параллели).

б) Частноортодромическая система координат..

Эта система координат для каждого участка маршрута своя. Одна из осей (ось S) направляется по ЛЗП данного участка в направлении полета, а вторая ось (ось Z) — вправо от нее.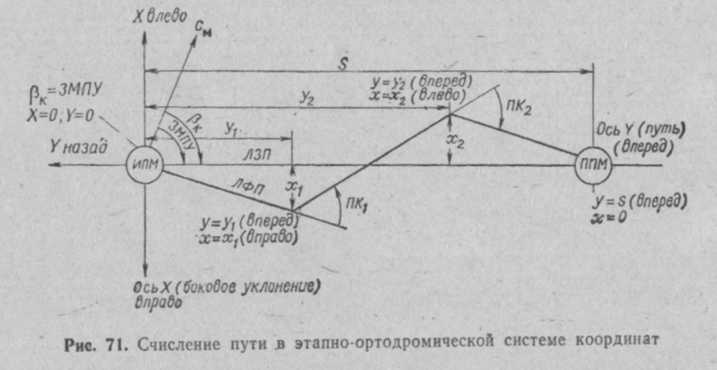

В зависимости от того, где расположено начало системы координат, различаются два варианта таких систем.

В первом случае начало системы координат, то есть точка, где обе координаты равны нулю, располагается в начальном ППМ данного участка маршрута, то есть в том ППМ, от которого летит ВС (рис.23.5,а).

Рис.23.5. Частноортодромические системы координат.

В этом случае координата Z совпадает с линейным боковым уклонением (ЛБУ), а координта S — с пройденным от ППМ расстоянием.

ЛБУ — это расстояние от МС до ЛЗП, измеренное, разумеется по
перпендикуляру к ЛЗП. Измеряется ЛБУ в километрах и считается
положительным при уклонении вправо и отрицательным при уклонении
влево, то есть знак ЛБУ соответствует знаку координаты Z. ЛБУ
соответствует английский термин cross-track error, сокращенно

обозначаемый как ХТЕ.

Пройденным расстоянием Sпр, называется расстояние между ППМ, от которого летит ВС, и проекцией МС на ЛЗП, то есть основанием упомянутого выше перпендикуляра. Обратите внимание, что Sпр измеряется вдоль ЛЗП и вовсе не является длиной пути ВС от ППМ до текущего МС. Если ВС развернется в середине участка и вернется в ППМ, S_пр будет равно нулю, независимо от того, какое расстояние пролетело ВС.

Такой выбор системы координат удобен для экипажа. Если он знает Z и S, то он знает, насколько ВС уклонилось от ЛЗП и насколько он удалился от ППМ. Зная длину участка маршрута, легко определить и оставшееся расстояние S_ОСТ. Очевидно, что для точного следования по ЛЗП необходимо стремиться выдерживать Z=0.

Во втором случае (рис.23.5, б) начало системы координат находится в конечном ППМ участка на котором летит ВС. Координата Zпо-прежнему соответствует ЛБУ, а координата S является отрицательной и равной по абсолютной величине оставшемуся расстоянию. Это тоже удобно. При выполнении полета S, оставаясь, отрицательной, увеличивается, то есть уменьшается по абсолютной величине. Момент, когда S станет равной нулю, будет соответствовать пролету ППМ.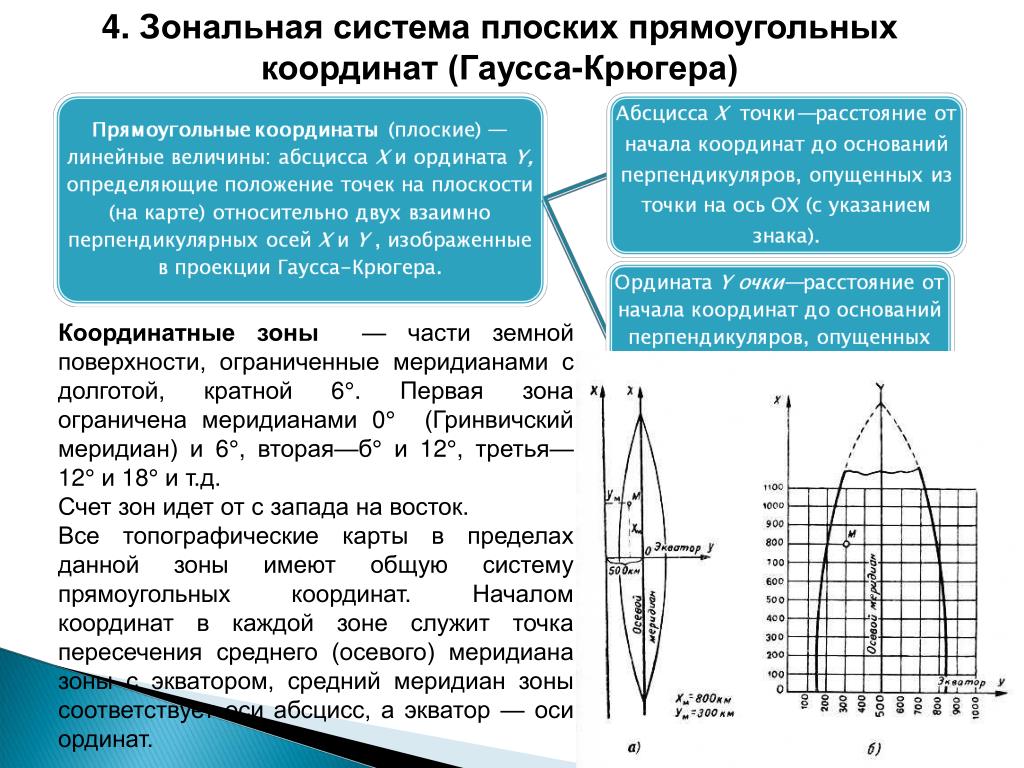

Существуют такие автоматизированные навигационные системы, выдающие экипажу S и Z, в которых сам экипаж может выбрать, какой вариант расположения начала системы частноортодромических координат будет использоваться. Но большинство современных ВС оборудовано системами, в которых однозначно предусмотрен второй из рассмотренных вариантов.

Системы координат и координатные преобразования для задач аэронавигации Текст научной статьи по специальности «Строительство и архитектура»

Ovil Aviation High Technologies

Vol. 20, No. 04, 2017

Б01: 10.26467/2079-0619-2017-20-4-88-97

СИСТЕМЫ КООРДИНАТ И КООРДИНАТНЫЕ ПРЕОБРАЗОВАНИЯ

ДЛЯ ЗАДАЧ АЭРОНАВИГАЦИИ

О.Н. СКРЫПНИК1

1 Иркутский филиал Московского государственного технического университета гражданской авиации, г. Иркутск, Россия

В статье рассмотрены основные типы систем координат, используемых для решения задач воздушной навигации, связанных с аэронавигационным обеспечением процессов самолетовождения и посадки. Приводятся основные требования, предъявляемые к выбору системы координат. Указаны противоречия, возникающие при выборе системы координат.

Рассмотрены локальные системы координат: прямоугольная, цилиндрическая и сферическая. Указаны достоинства и недостатки данных систем координат, процессы навигации, при которых их применение целесообразно. Приведены прямые и обратные координатные преобразования между локальными системами координат.

Показаны основные особенности применения глобальных систем координат, связанные с выбором модели фигуры Земли и проблемами ее математического описания. Даны основные сведения об общеземных эллипсоидах и их параметрах. Раскрыты понятия геоида, волны геоида, референц-эллипсоида. Показана необходимость перехода к общеземному эллипсоиду и глобальным системам отсчета и этапы такого перехода. Приведены общие сведения о Международной системе отсчета ITRS и Международной земной отсчетной основе 1ТЯР. Выделены отличия в определении пространственных координат объектов в этих системах отсчета. Указаны отличия в областях применения систем ПЗ-90 и СК-2011 и их аналогов WGS-84 и NAD-83.

Рассмотрены особенности глобальных геодезической и геосферической (ортодромической) систем координат, их достоинства и недостатки. Приведены прямые и обратные координатные преобразования для глобальных систем координат, а также выражения, устанавливающие связь между геоцентрическими и топоцентрическими системами координат.

Ключевые слова: система координат, геоид, общеземной эллипсоид, координатные преобразования, локальная система координат, геодезическая система координат, аэронавигация.

ВВЕДЕНИЕ

Используемые в задачах аэронавигационного обеспечения системы координат предназначены для определения местоположения и параметров движения воздушных судов (ВС), а также математического описания процессов навигации. При этом система координат должна удовлетворить ряду требований [1]:

— решение навигационных задач с требуемой точностью;

— охват необходимой по площади территории земной поверхности или объема воздушного пространства, в пределах которых решаются навигационные задачи;

— наглядность и простота отображения и восприятия информации о местоположении объекта в системе координат;

— простота математических соотношений, описывающих процесс перемещения ВС.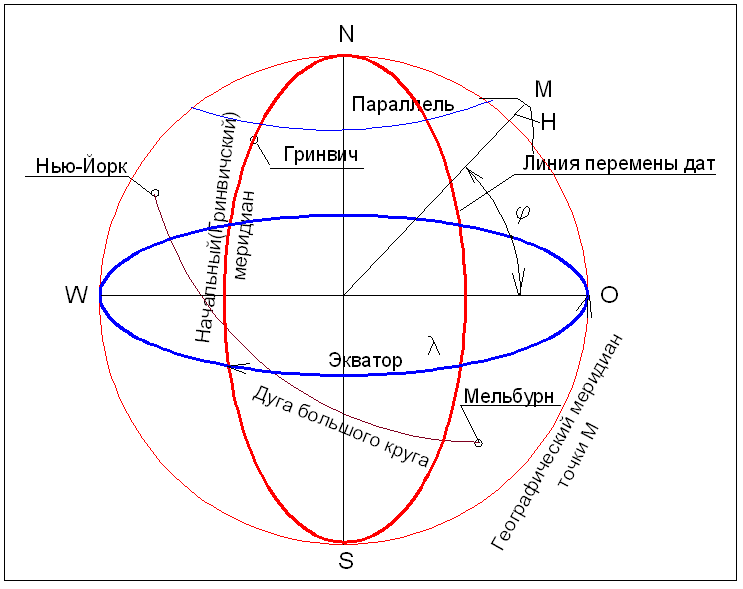

Перечисленные требования противоречивы. Так, выбор системы координат, единой для

всей земной поверхности, неизбежно приводит к сложным математическим соотношениям, а системы координат, позволяющие решать навигационные задачи по сравнительно простым математическим зависимостям, обеспечивают приемлемую точность лишь в ограниченной области пространства. Поэтому на практике используются различные системы координат, в каждой из которых обеспечивается наиболее эффективное решение частных навигационных задач.

Для решения задач навигации ВС относительно земной поверхности в настоящее время используются связанные с земной поверхностью локальные и глобальные системы координат.

Настоящая статья посвящена рассмотрению особенностей локальных и глобальных систем координат, применяемых в воздушной навигации, взаимосвязи между системами координат, а также эволюции представлений глобальных систем координат.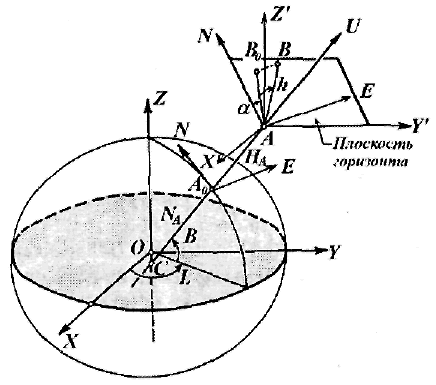

Vol. 20, No. 04, 2017

СМ! Aviation High Technologies

ЛОКАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ И КООРДИНАТНЫЕ ПРЕОБРАЗОВАНИЯ

Локальные системы координат охватывают ограниченную часть земной поверхности и используются при перемещениях ВС на расстояния до 400-450 км, когда кривизной земной поверхности можно пренебречь без ущерба для точности решения навигационной задачи. В таких системах координат работают, например, системы посадки ILS, системы ближней навигации VOR/DME, TACAN, российская система РСБН.

К локальным относятся цилиндрическая, сферическая и прямоугольная системы координат (рис. 1) [2], начало которых находится в точке на поверхности Земли. Поэтому данные системы также являются топоцентрическими.

Координатами т.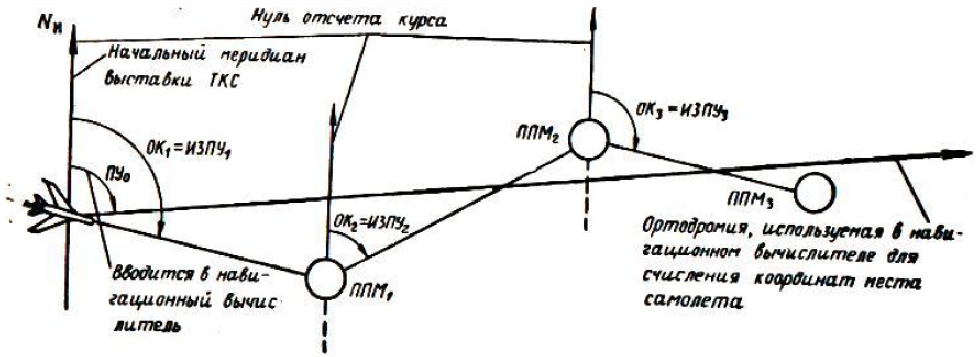 М в указанных системах координат являются: в прямоугольной системе (рис. 1, а) — координаты x, y, z; в цилиндрической (рис. 1, b) — проекция r на горизонтальную плоскость радиус-вектора р, проведенного из начала системы координат в т. М, азимут 0, высота z; в сферической (рис. 1, с) — расстояние р (радиус-вектор) до т. М из начала системы координат, азимут 0, угол места в

Азимут отсчитывается в горизонтальной плоскости от направления оси ОХ, которая, как правило, ориентирована в направлении истинного севера, до проекции r радиус-вектора р на горизонтальную плоскость. Ось OZ ориентирована по нормали к земной поверхности в точке О.

Локальные системы координат находят широкое применение при полетах на небольшие (до 500 км) расстояния, управлении ВС на этапах взлета и посадки, определении местоположения ВС относительно ориентиров.

а) Ь) с)

Рис. 1. Локальные системы координат Fig. 1. The local coordinate system

При решении задач навигации часто возникает необходимость пересчета координат ВС или других объектов (например, радиомаяков) из одной системы координат в другую. Это связано с тем, что различные технические средства навигации могут работать и выдавать информацию в разных системах отсчета, а бортовая система отображения информации или алгоритмы комплексной обработки навигационной информации, реализуемые в бортовой системе самолетовождения современных ВС, предполагают использование общей системы координат [3].

Преобразования из цилиндрической в прямоугольную систему координат имеют вид [2]

х = rcos0; y = rsin0; z = z.

Сivil Aviation High Technologies

Vol. 20, No.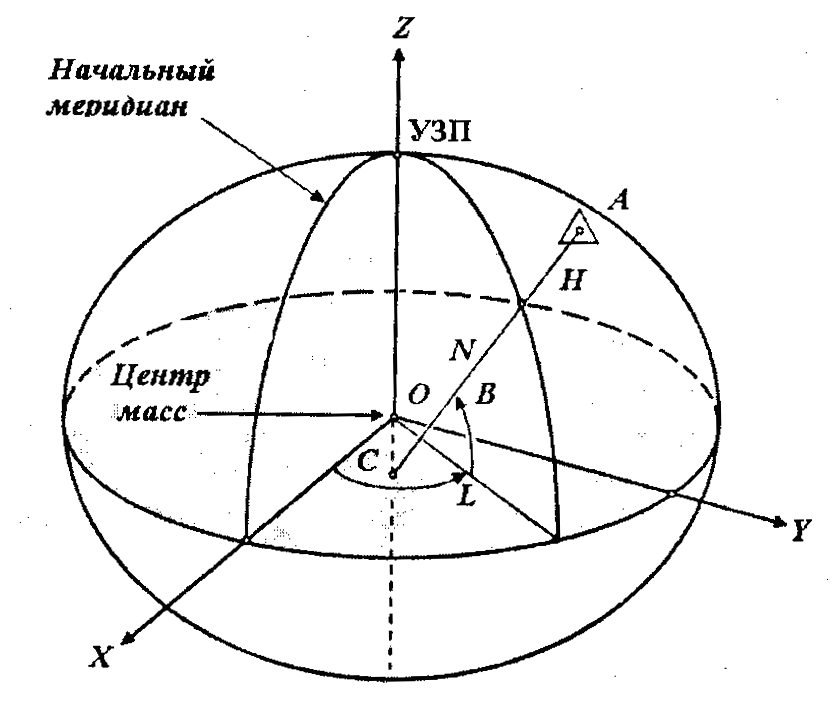 04, 2017

Обратные преобразования удовлетворяют следующим выражениям:

0 = arctg — ; x

z = z.

Преобразования координат из сферической в прямоугольную систему координат имеют вид [2]

х = р cosв cos0; у = р cosв sm@; z = р smp.

Обратные преобразования удовлетворяют следующим выражениям:

p = yjx2 + y2 + z2

0 = arctg

У.

ß = arctg

2 . 2 X + —

Достоинствами локальных систем координат являются достаточно простые математические соотношения, описывающие процессы перемещения ВС, наглядность отображения и восприятия информации о местоположении ВС относительно начала системы координат, простые и точные координатные преобразования из одной системы в другую. Основной недостаток систем — охват незначительной части земной поверхности. Поэтому данные системы координат используются для решения задач ближней навигации, при заходе на посадку и посадке.

ГЛОБАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ И ИХ ЭВОЛЮЦИЯ

Глобальные системы координат охватывают всю поверхность земли. Фигура Земли, а значит, и земная поверхность, имеет сложную форму. К сожалению, не существует системы координат, абсолютно точно учитывающей фигуру Земли при описании процессов навигации относительно земной поверхности в любом ее районе. Поэтому используют различные аппроксимации фигуры Земли для удовлетворения требований по точности при решении геодезических, картографических или навигационных задач [4].

Использование современных технологий измерения параметров Земли, развитие спутниковой навигации, а также требования к интероперабельности воздушного пространства, вызвали значительные изменения в подходах к описанию фигуры Земли и точности такого описания. В результате в настоящее время применяются системы координат как для решения задач геодезии и картографии, так и для решения задач воздушной и космической навигации.

Системы первого типа, использующиеся уже давно, ориентированы на раздельное определение положения объектов на поверхности земли (горизонтальное двумерное пространство) и по вертикали (ортометрическая высота, отсчитываемая от среднего уровня Мирового океана, а системы второго типа — на определение положения объектов в трехмерном пространстве [5].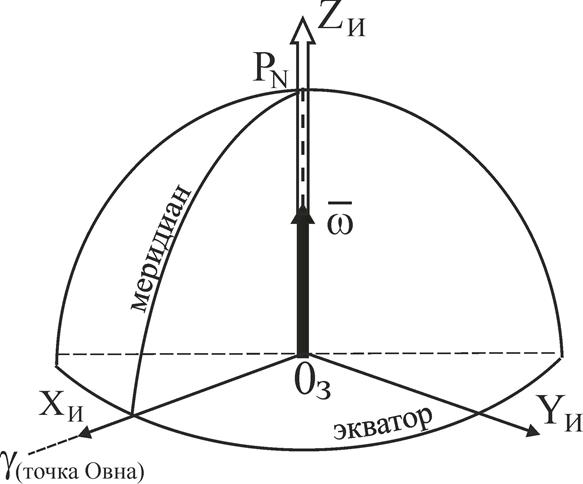 В обоих случаях нужна наиболее точная аппроксимация фигуры Земли и ее поверхности.

Наиболее близким по форме к земной поверхности (рис. 2, а) является геоид (рис. 2, б) -поверхность, всюду нормальная силе тяжести (поверхность, на которой атмосферное давление постоянно и равно 760 мм рт. ст.) и совпадающая с уровнем Мирового океана в его спокойном состоянии. Вследствие таких эффектов, как изменение атмосферного давления, температуры, господствующих ветров и течений, вариаций плотности (солености) водных масс, средний уровень Мирового океана может отличаться от поверхности геоида на метр и более.

Vol. 20, No. 04, 2017

Ovil Aviation High Technologies

a) 6) в)

Рис.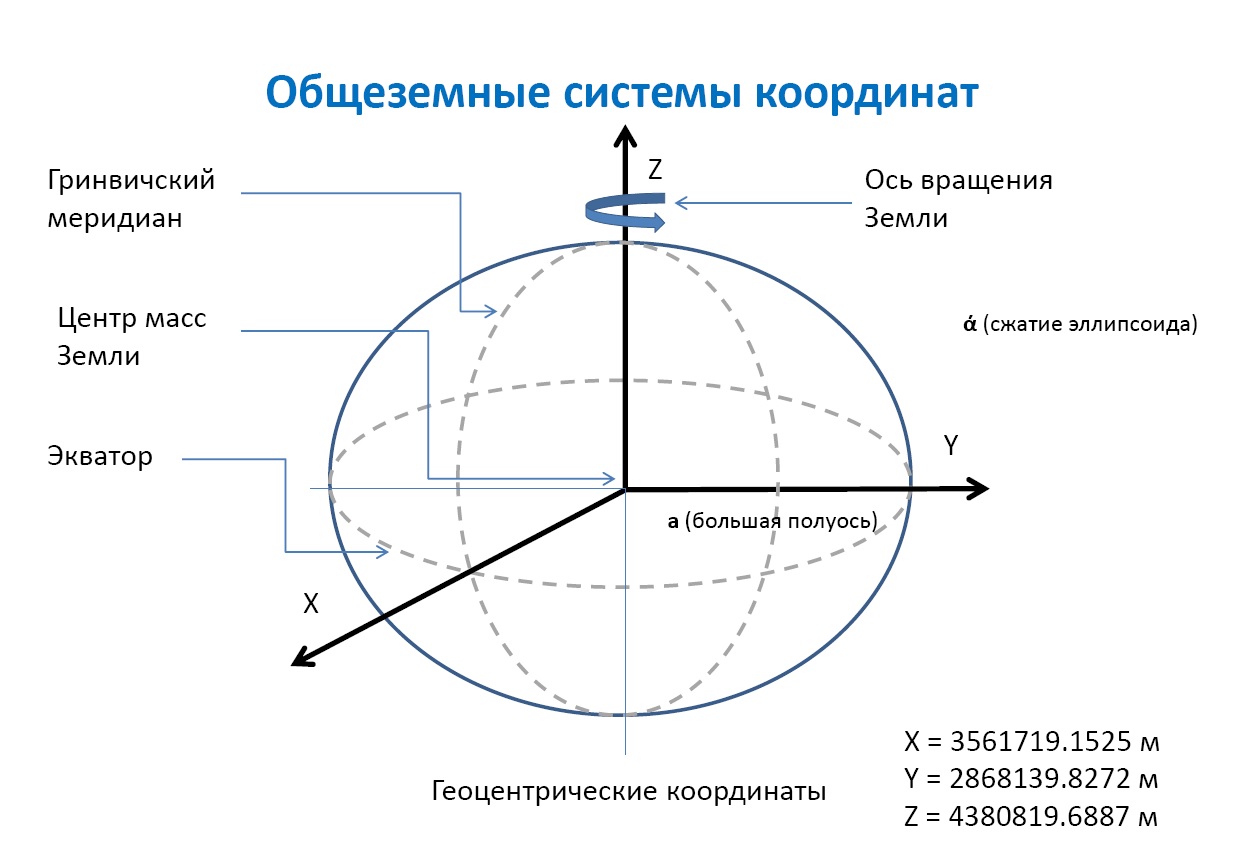 2. Аппроксимации фигуры Земли Fig. 2. Approximation of the Earth’s shape

Поверхность геоида хотя и является гладкой по сравнению с физической поверхностью земли, но все же имеет неправильную форму. Это вызвано неравномерным расположением гравитационных масс в теле Земли, вследствие чего происходит отклонение отвесных линий.

Для создания глобального геоида была разработана модель гравитации Земли (Earth Gravitational Model) 1996 года — EGM96 и принят геоид WGS-84 (EGM96), обеспечивающий точность не хуже 1 м в пунктах, где измерялась гравитация. Действующей, более точной и полной, является модель 2008 года EGM2008 [6].

Геоид не удается описать математически, поэтому для решения практических задач на поверхности земли она представляется математически описанной геометрической фигурой -эллипсоидом (рис. 2, в). Подбирая параметры эллипсоида, можно в большей или меньшей степени приблизить его к геоиду в разных его частях. Однако невозможно подобрать эллипсоид, точно совпадающий с геоидом в пределах всей земной поверхности. Разность между поверхностями геоида и эллипсоида (называемая волной геоида) (рис. 3, а) может достигать порядка 100 м и более [7]. Информация о волне геоида необходима для определения превышений аэродромов, зон приземления и отрыва на взлетно-посадочной полосе или зон конечного этапа захода на посадку и взлета на вертодромах.

До 1964 года каждая страна подбирала параметры эллипсоида, приближенного к геоиду на территории этой страны. Такой эллипсоид получил название референц-эллипсоида (рис. 3, б).

Референц-эллипсоиды принимались для обработки геодезических измерений законодательно. Исторически сложилось так, что в разные времена и в разных странах были приняты и законодательно закреплены различные эллипсоиды, и их параметры не совпадали между собой.

а) б)

Рис. 3. Геоид и референц-эллипсоид Fig. 3. Geoid end Local Ellipsoid

В России/CCCP использовался эллипсоид Красовского с параметрами: большая полуось а = 6378245 м, малая полуось b = 6356863 м, сжатие 1:298,3. В США и Канаде использовали

Сivil Aviation High Technologies

Vol. 20, No. 04, 2017

эллипсоид Кларка (Clarke 1880) с параметрами: большая полуось а = 6378249 м, сжатие 1:295,0. Во многих странах Западной Европы и некоторых государствах Азии был принят эллипсоид Хейфорда, а в Индии и странах Южной Азии использовали эллипсоид Эвереста [6].

Увеличение дальности полетов ВС, появление спутниковых систем навигации и развитие систем управления полетом (типа Flight Management System, FMS) выявило ряд острых проблем при использовании референц-эллипсоидов, например, скачки в измеряемых координатах при переходах ВС между воздушными пространствами соседних государств. Поэтому были проведены работы по установлению общеземного эллипсоида, подходящего для использования всеми государствами. В результате был принят общеземной эллипсоид Geodetic Reference System 1980 (GRS-80).

Геодезическое положение объекта относительно земной поверхности определяется в связанной с Землей системе отсчета (Terrestrial Reference System, TRS). Эта система характеризуется определенными физическими константами (гравитационная постоянная, большая полуось эллипса, скорость вращения Земли, скорость света и др.), моделями (например, вращения Земли) и системой координат, в которой однозначно определяются координаты точек [8].

Такой системой координат может быть, например, прямоугольная система координат OXYZ, начало которой т. О находится в центре масс Земли, координатные оси OX и OY лежат в плоскости экватора, ось OZ совпадает с осью вращения Земли (рис. 4).

Эта система координат вращается со скоростью вращения Земли и 3.0-координаты точки в ней — это положение точки относительно центра масс Земли.

3.0-координаты точки можно также определять на поверхности эллипсоида в виде угловых параметров — широты и долготы, и высоты над поверхностью эллипсоида.

В 1991 году в качестве единой принята Международная земная система отсчета ITRS (International Terrestrial Reference System). В США в качестве земной системы отсчета используется WGS-84 (World Geodetic System). WGS-84 рекомендована ИКАО для использования в качестве международной системы отсчета.

Связь Международной земной системы отсчета ITRS с земной поверхностью реализована через Международную земную от-счетную основу ITRF (International Terrestrial Reference Frame) .

ITRF представляет собой набор физических точек (более 4000 по всей земной поверхности) с точно определенными с помощью спутниковых технологий (система GPS) 3.0-координатами. Поэтому основой для ITRF также является общеземной эллипсоид WGS-84. Текущая версия — ITRF2008 [8].

В России в качестве земной системы отсчета используется система «Параметры земли 1990 года» (ПЗ-90) с параметрами полуосей а = 6 378 136 м, b = 6 356 777 м, сжатие 1:298,25784 [9]. Ее текущая версия — ПЗ-90.11, установленная в 2012 году. За отсчетную поверхность в этой системе отсчета принята поверхность эллипсоида ПЗ-90.11. До 1.01.2017 г. вместе с ПЗ-90.11 в СССР/России использовался эллипсоид Красовского.

В России в качестве геодезической системы отсчета с 2012 году введена система координат СК-2011. Ее предыдущими версиями были СК-42 и СК-95, в которых в качестве отсчет-ной поверхности использовался эллипсоид Красовского.

Рис. 4. Связанная с общеземным эллипсоидом 3D-система координат (OXYZ) Fig. 4. Associated with the global ellipsoid 3D-Cartesian (OXYZ) system

Vol. 20, No. 04, 2017

Ovil Aviation High Technologies

В США в качестве геодезической системы отсчета используется NAD-83 (North American Datum 1983) [10]. В качестве отсчетной выбрана поверхность эллипсоида GRS-80 (практически идентичного WGS-84) с параметрами а = 6 3 78 137 м, b = 6356777 м, сжатие 1:298,257.

Системы координат NAD-83 и СК-2011 предназначены для выполнения геодезических и картографических работ. Эти системы удобны для навигации ВС относительно наземных станций и ориентиров, координаты которых привязаны к земной поверхности.

Общеземные геоцентрические системы координат ПЗ-90.11 и WGS-84 предназначены для использования в целях геодезического обеспечения орбитальных полетов и решения навигационных задач, прежде всего по данным спутниковых систем навигации ГЛОНАСС и GPS.

В современных бортовых FMS обработка информации и ее выдача на многофункциональные индикаторные приборы (типа ND или PFD) осуществляется в глобальной геодезической системе координат ПЗ-90.11 (Россия) или WGS-84 (рис. 5, а). В ней координатами ВС являются геодезическая широта В и геодезическая долгота L, а также высота над поверхностью эллипсоида (абсолютная высота по принятой в России терминологии, или QNH — по международной терминологии). При этом геодезическая широта представляет собой угол между нормалью, проведенной через точку М к земной поверхности, и плоскостью экватора.

Рис. 5. Глобальные геоцентрические системы координат Fig. 5. The global geocentric coordinate system

Использование данной системы координат позволяет решать задачи аэронавигации с высокой точностью независимо от расстояний, на которые перемещается ВС. Однако процессы навигации в этой системе координат описываются достаточно сложными выражениями, которые реализованы в компьютерах систем самолетовождения только современных ВС.

До недавнего времени основной для решения задач воздушной навигации была ортодро-мическая система координат, в которой фигура Земли аппроксимируется сферой. По принятой аппроксимации фигуры Земли ортодромическая система координат аналогична геосферической (рис. 5, б), но отличается произвольно устанавливаемыми условными полюсами и условным экватором (главной ортодромией).

Местоположение ВС в геосферической системе координат определяется геосферическими широтой ф и долготой X. При этом геосферическая широта ф т. М отличается от геодезической широты В тем, что она представляет собой угол между радиус-вектором, проведенным из центра сферы в т. М, и плоскостью экватора. Понятия и способ отсчета геосферической X и геодезической долготы L совпадают.

Ovil Aviation High Technologies

Vol. 20, No. 04, 2017

При решении навигационных задач в геосферической системе координат возникают методические погрешности определения местоположения ВС, вызванные аппроксимацией фигуры Земли сферой. Максимальная разность между геодезической и геосферической широтой наиболее значительна в средних широтах и составляет (В — ф)тах = 11,6 угл. мин, убывая по мере приближения к полюсам или экватору. При этом геосферическая широта всегда меньше геодезической (кроме полюсов и экватора), а геодезическая и геосферическая долгота точки совпадают.

КООРДИНАТНЫЕ ПРЕОБРАЗОВАНИЯ В ГЛОБАЛЬНЫХ СИСТЕМАХ КООРДИНАТ

Связь между координатами ВС в прямоугольной системе координат 0ХУ2, начало которой находится в центре масс Земли, и геодезическими (пространственными эллипсоидальными) координатами определяется выражениями

х = (N+H)cosBcosL,

y = (N+H)cosBsinL, «Ja2 — b2

где H — высота над поверхностью эллипсоида; e =

z = (N+H-e2N)sinB,

эксцентриситет земного эллипсои-

2 2 —1/2

да; N = a • (1— e sin B) — радиус кривизны первого вертикала.xr7yF)

1 — e2

N + H

L = Arctg —, [-71.71 ],

H =

cosB

— N,

где Arctg(*) — круговое значение арктангенса с учетом квадрантов.

Следует отметить, что данное преобразование выполняется итерационным методом, но сходимость достигается достаточно быстро.

Для пересчета координат объектов в локальную топоцентрическую систему координат (OXjYjZJ), геодезически привязанную к заданной точке Земли (Bo, Loo, Но) (рис. 6), из геодезических координат (B, L, h) сначала производится пересчет в геоцентрические прямоугольные координаты (x, y, z), связанные с центром Земли, а затем выполняется преобразование

Рис. 6. Топоцентрическая локальная прямоугольная система координат Fig. 6. The local topocentric Cartesian system

x Х0

Ул = M ■ У — Уо

Z л z — zo

где Хо, уо, Zo — геоцентрические прямоугольные координаты начала локальной системы координат,

Vol. 20, No. 04, 2017

Civil Aviation High Technologies

M =

-sinLn

cosLn

-cosL0sinB0 — sinL0sinB0

cosL0cosB0

sinL0 cos B0

cosB0 sinB

— матрица преобразования.

Обратный пересчет координат из локальной OXлYлZл в геоцентрическую систему координат ОХУ2 осуществляется в соответствии с выражением

x ХЛ Х0

У = MT Ул + Уо

z z л zo

— т

где M — транспонированная матрица.

Для точки, находящейся на поверхности земной сферы, координатные преобразования из геосферической системы координат в прямоугольную ОХУ2 имеют вид

х = R cosp cosk; и обратное преобразование

y = R cosp sink;

z = R siny

R =7×2 + y2 + z2;

Ф = arctg

Ä = arctg —. x

Пересчет геодезической широты в геосферическую может быть выполнен и по приближенной формуле ф = B — 8’39″sm2B.

ЗАКЛЮЧЕНИЕ

Выбор системы координат, единой для всей земной поверхности, неизбежно приводит к сложным математическим соотношениям, а системы координат, позволяющие решать навигационные задачи по сравнительно простым математическим зависимостям, обеспечивают приемлемую точность лишь в ограниченной области пространства. Поэтому на практике используются различные системы координат, в каждой из которых обеспечивается наиболее эффективное решение частных навигационных задач.

Для решения задач навигации ВС относительно земной поверхности в настоящее время используются связанные с земной поверхностью локальные и глобальные системы координат. Между рассмотренными системами координат имеется однозначная связь, что позволяет приводить информацию от различных средств навигации в общую систему для реализации алгоритмов комплексной обработки.

Проведенный анализ локальных и глобальных систем координат, используемых в воздушной навигации, позволил установить их основные особенности и области применения.

СПИСОК ЛИТЕРАТУРЫ

1. Скрыпник О.Н. Радионавигационные системы воздушных судов: учебник. М.: ИНФРА-М, 2014. 248 с.

2. Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). М.: Наука, 1974. 832 с.

Civil Aviation High Technologies

Vol. 20, No. 04, 2017

3. Скрыпник О.Н. Межсамолетная навигация при управлении воздушным движением. дисс. на соискание ученой степени доктора технических наук / Московский государственный технический университет гражданской авиации. М., 2010.

4. Радионавигационный план Российской Федерации. Утвержден приказом Минпром-торга России от 28 июня 2015 г. № 2123. 142 с. [Электронный ресурс]. URL: http://docs.cntd.ru/document/4560343228 (дата обращения 03.02.2017).

5. Постановление Правительства Российской Федерации от 28.12.2012 № 1463. О единых государственных системах координат [Электронный ресурс]. URL: http://gis-lab.info/docs/law/ statecoord-2012.doc (дата обращения 3.02.2017).

6. Doc 9674 AN/946. World Geodetic System — 1984 (WGS-84) Manual. International Civil Aviation Organization, Second Edition, 2002, р. 134.

7. Moritz. H. Geodetic Reference System 1980 [Электронный ресурс]. URL: http://geodeticscience.org/course/refpapers/00740128.pdf (дата обращения 3.02.2017).

8. ITRF 2008. URL: http://itrf.ensg.ign.fr/ITRF_solutions/2008/ (дата обращения 26.02.2017).

9. Параметры Земли 1990 года (ПЗ-90.11). Справочный документ. Военно-топографическое управление Генерального штаба Вооруженных сил Российской Федерации, М., 2014. 52 с.

10. 2014 Federal Radionavigation Plan. [Электронный ресурс]. National Technical Information Service, Springfield, Virginia 22161 DOT-VNTSC-OST-R-15-0 URL: https://www.navcen. uscg.gov/ pdf/Federal RadionavigationPlan2014.pdf (дата обращения 3.02.2017).

СВЕДЕНИЯ ОБ АВТОРЕ

Скрыпник Олег Николаевич, доктор технических наук, профессор, заместитель директора Иркутского филиала МГТУ ГА о учебно-научной работе, [email protected].

COORDINATE SYSTEMS AND TRANSFORMATIONS FOR AIR NAVIGATION TASKS

Oleg N. Skrypnik1

1Irkutsk Branch of Moscow State Technical University of Civil Aviation, Moscow, Russia

ABSTRACT

The main types of coordinate systems, used for air navigation tasks solving that are connected with aeronautical flight control and landing provisioning are examined in the article. The basic requirements for the coordinate system choice as well as the conflicts that appear while choosing are stated.

Local coordinate systems have been studied: orthogonal, cylindrical and spherical. Advantages and disadvantages of these coordinate systems, the navigation processes at which their application is rational are mentioned. Direct and backward coordinate transformations between local coordinate systems have been shown.

Essential distinctive features of global coordinate systems’ appliance connected with the Earth’s model figure choosing and its mathematical description problems are shown. Basic information about the global ellipsoids and its parameters is presented. The concepts of geoid, geoid wave and reference-ellipsoid have been studied. The necessity of transitioning to the global ellipsoid and global reference systems as well as the stages of such transitioning are shown. Information about the ITRS and ITRF is given. Differences in determining the objects space coordinates in these reference systems are described. Differences in ПЗ-90 and СК-2011 application areas and their prototypes WGS-84 and NAD-83 ones are specified.

The peculiarities of global geodesic and geospheric (orthodromic) coordinate systems are examined as well as their advantages and disadvantages. Direct and backward coordinate transitions for global coordinate systems and the expressions which set the connection between geocentric and topocentric coordinate systems are illustrated.

Vol. 20, No. 04, 2017

Ovil Aviation High Technologies

Key words: coordinate system, geoid, global terrestrial ellipsoid, coordinate transformations, local coordinate system, geodetic coordinate system, aeronavigation.

1. Skrypnik O.N. Radionavigatsionnye sistemyi vozdushnyih sudov [Radionavigation systems of aircrafts]. Moscow, INFRA-M, 2014, 248 p. (in Russian)

2. Korn G., Korn T. Spravochnikpo matematike [Handbook of mathematics] (dlya nauchnyih rabotnikov i inzhenerov). Moscow, Nauka, 1974, 832 p. (in Russian)

3. Skrypnik O.N. Mezhsamoletnaya navigatsiya pri upravlenii vozdushnyim dvizheniem [Interaircraft navigation for air traffic control]. PhD work. Moskovskiy gosudarstvennyiy tehnicheskiy universitet grazhdanskoy aviatsii. Moscow, 2010. (in Russian)

4. Radionavigatsionnyiy plan Rossiyskoy Federatsii [Radionavigational plan or Russian Federation]. Approved by the order of the Ministry of Industry and Trade of RF from 28.06. 2015. no. 2123, 142 p. URL: http://docs.cntd.ru/document/4560343228 (accessed: 03.02. 2017). (in Russian)

5. Postanovlenie Pravitelstva Rossiyskoy Federatsii ot 28.12.2012 № 1463. O edinyih gosudarstvennyih sistemah koordinat. Available at: http://gis-lab.info/docs/law/statecoord-2012.doc (accessed: 3.02.2017). (in Russian)

6. Doc 9674 AN/946. World Geodetic System — 1984 (WGS-84) Manual. International Civil Aviation Organization, Second Edition, 2002, 134 p.

7. Moritz H. Geodetic Reference System 1980. Available at: http://geodeticscience. org/course/refpapers/00740128.pdf (accessed 3.02.2017).

8. ITRF 2008. Available at: http://itrf.ensg.ign.fr/ITRF_solutions/2008/ (accessed 26.02.2017).

9. Parametry Zemli 1990 goda (PZ-90.11) [The Earth’s parameters (PZ-90.11)]. Spravochnyiy dokument. Voenno-topograficheskoe upravlenie Generalnogo shtaba Vooruzhennyh sil Rossiyskoy Federatsii. Moscow, 2014, 52 p. (in Russian).

10. 2014 Federal Radionavigation Plan. National Technical Information Service, Springfield, Virginia 22161 DOT-VNTSC-OST-R-15-0. Available at:https://www.navcen. uscg.gov/pdf/Federal RadionavigationPlan2014.pdf (accessed 3.02.2017).

Oleg N. Skrypnik, Doctor of Technical Sciences, Full Professor, Deputy Director of Educational and Scientific Work of Irkutsk Branch of Moscow State Technical University of Civil Aviation, skripnikon@yandex .ru.

REFERENCES

INFORMATION ABOUT THE AUTHOR

Поступила в редакцию Принята в печать

20.01.2017 25.05.2017

Received

Accepted for publication

20.01.2017 25.05.2017

Системы координат, применяемые в навигации (сферическая, полярная, ортодромическая)

Экзаменационные вопросы по аэронавигации для студентов специализации ОЛР (2 семестр).

Системы координат, применяемые в навигации (сферическая, полярная, ортодромическая).

Если очень высокая точность решения навигационных задач не требуется, то Землю можно рассматривать как сферу. В этом случае используется нормальная сферическая система координат, полюсы которой совпадают с географическими полюсами нашей планеты, т.е. точками, в которых ось вращения Земли пересекает ее поверхность. Система координат на сфере строится с помощью больших кругов.

Большим кругом (Great Circle, G/C) называется окружность, образующаяся в результате сечения сферы плоскостью, проходящей через центр сферы.

Радиус большого круга равен радиусу самой сферы. Он называется большим, поскольку на сфере нельзя нарисовать окружность с радиусом еще большим. Все другие круги на сфере называются малыми.

Экватор (equator) –- большой круг, плоскость которого перпендикулярна оси вращения Земли (рис. 2.5).

Рис. 2.5. Сферические координаты

Меридиан(meridian) – большой круг, плоскость которого проходит через ось вращения Земли.

Параллель(parallel) – малый круг, плоскость которого перпендикулярна оси вращения (параллельна экватору).

Экватор на Земле один, а меридианов бесчисленное множество – ведь через каждую точку можно провести свой меридиан. Все они одинаковы и равноправны, поэтому условно один из них выбирают в качестве начального.

Широтой φ (сферической широтой) точки на поверхности земной сферы называется угол, заключенный между плоскостью экватора и направлением из центра сферы в данную точку.

Широта изменяется от 90° южной широты до 90° северной широты. При расчетах по формулам северную широту можно считать положительной, а южную отрицательной. На экваторе широта равна нулю, а на географических полюсах ±90°.

Долготой λ (сферической долготой) точки на поверхности сферы называется двугранный угол, заключенный между плоскостями начального меридиана и меридиана данной точки.

Этот угол можно показать как плоский в плоскости экватора (рис.2.5). В качестве начального меридиана используется Гринвичский меридиан (Greenwich meridian).

Долгота изменяется от 180° западной долготы до 180° восточной. При расчетах по формулам им также можно приписывать знаки соответственно минус и плюс (или наоборот, как это принято, например в США).

Единицами измерения широты и долготы являются угловые градусы, минуты и секунды, а иногда и их десятичные доли (десятые, сотые и т.д.). За рубежом используются следующие буквенные обозначения:

N (north) – север, S (south) – юг, E (east) – восток, W (west) – запад.

Одни и те же значения широты и долготы в документах аэронавигационной информации при выполнении различных навигационных расчетов могут быть представлены по-разному:

37° 23¢ 12¢¢ с.ш. = N37° 23.2¢ = +37.38667°.

134° 45¢ 45¢¢ з.д. = W134° 45.75¢ = -134.7625°.

Ни направление нормали к поверхности эллипсоида, ни направление к центру Земли непосредственно приборами измерены быть не могут, поэтому не могут быть непосредственно измерены ни геодезическая, ни сферическая широты. Непосредственно можно определить лишь направление отвесной линии. В связи с этим используется также астрономическая система координат, в которой астрономическая широта – угол, заключенный между плоскостью экватора и отвесной линией в данной точке. Различия между геодезическими, нормальными сферическими и астрономическими координатами невелики – не более нескольких угловых минут. Поэтому, когда различие между этими системами координат не играет роли, их объединяют общим названием — географические координаты.

Кроме особо оговоренных случаев, в данном учебном пособии будем принимать Землю за сферу и в качестве географических использовать сферические широту и долготу.

Длина дуги большого круга (в частности, экватора и меридиана) протяженностью в 1° в среднем равна 111,2 км. Именно в среднем, потому, что на самом деле меридиан является не окружностью, а эллипсом и длина дуги в 1° различна на разных широтах. Соответственно, длина дуги в одну минуту составляет в среднем 1,853 км, а секунды – около 31 м.

Длина параллели, которая является не большим, а малым кругом, уменьшается по мере приближения к полюсу, т.е. с увеличением широты. Длина дуги в 1° на параллели с широтой j составляет 111,2cos j .

Расстояния на земной поверхности измеряются в метрах, километрах, а за рубежам часто и в морских милях (nautical miles, NM). Величина морской мили соответствует средней длине одной минуты меридиана. В морской и воздушной навигации принято фиксированное значение длины морской мили (м.мили) – 1852 м, ведь единица измерения не должна быть разной на различных широтах.

Высоты измеряются в метрах, за рубежом часто в футах.

1 м.миля = 1,852 км; S км =1,852 S м.миль.

1 м = 3,2808 фт; Н фт = 3,2808 Н м.

2.Ортодромические системы координат.

Ортодромические системы (grid systems) являются обобщающим случаем сферических координат. Вместо «настоящих» меридианов и параллелей, как в географических системах, используются меридианы и параллели условные, наиболее удобно расположенные относительно маршрута полета.

а) Главноортодромические.

Начало обычно размещается в исходным пунктом маршрута (ИПМ), а одну из осей, называемую главной ортодромией, направляют вдоль маршрута, например так, чтобы она проходила через КПМ либо вблизи всех ППМ. Главная ортодромия является экватором такой условной сферической системы координат. Вторая ось направляется вправо от направления полета (рис.2.14).

Координаты могут быть выражены как в линейной мере (в километрах), так и в угловой мере аналогично широте и долготе.

Рис. 2.14. Главноортодромическая система координат

Преимущество главноортодромической системы состоит в том, что она используется одна на весь маршрут. Можно заранее рассчитать в этой системе координаты ППМ и близко расположенных радиомаяков, определять МС. Недостаток же ее заключается в том, что по значениям координат, например Х и У, невозможно судить непосредственно о расположении ВС относительно ЛЗП. Даже при точном следовании по маршруту обе координаты будут изменяться, поскольку маршрут имеет изломы и участки маршрута, как правило, не совпадают ни с одной из осей. Вместе с тем, такие системы координат применяются в пилотажно-навигационных комплексах некоторых типов ВС. Система координат такого типа может использоваться и при внемаршрутных полетах, когда полеты производятся в ограниченном районе, например, при выполнении авиационных работ. В этом случае начало системы координат располагают в одной из точек этого района (например, на аэродроме вылета), а оси направляют по меридиану и перпендикулярно к нему (по касательной к параллели).

б) Частноортодромическая система координат..

Эта система координат для каждого участка маршрута своя. Одна из осей (ось S) направляется по ЛЗП данного участка в направлении полета, а вторая (ось Z) – вправо от нее.

В зависимости от того, где расположено начало системы координат, различаются два варианта таких систем.

Рис. 2.15. Два варианта частноортодромических систем координат

В этом случае координата Z совпадает с линейным боковым уклонением (ЛБУ), а координта S – с пройденным от ППМ расстоянием.

ЛБУ – это расстояние от МС до ЛЗП, измеренное, разумеется, по перпендикуляру к ЛЗП. Измеряется ЛБУ в километрах и считается положительным при уклонении вправо и отрицательным при уклонении влево, то есть знак ЛБУ соответствует знаку координаты Z. ЛБУ соответствует английский термин cross-track error, сокращенно обозначаемый как XTE (здесь буква Х заменяет слово cross, которое означает и «крест», и «поперечный»).

Пройденным расстоянием S_пр называется расстояние между ППМ, от которого летит ВС, и проекцией МС на ЛЗП, то есть основанием упомянутого перпендикуляра. Обратите внимание, что S_пр измеряется вдоль ЛЗП и вовсе не является длиной пути ВС от ППМ до текущего МС. Если ВС развернется в середине участка и вернется в ППМ, S_пр будет равно нулю, независимо от того, какое расстояние пролетело ВС.

Такой выбор системы координат удобен для экипажа. Если он знает Z и S, то он знает, насколько ВС уклонилось от ЛЗП и насколько он удалился от ППМ. Зная длину участка маршрута, легко определить и оставшееся расстояние S_ост. Очевидно, что для точного следования по ЛЗП необходимо стремиться выдерживать Z=0.

Во втором случае (рис.2.15, б) начало системы координат находится в конечном ППМ участка на котором летит ВС. Координата Z по-прежнему соответствует ЛБУ, а координата S является отрицательной и равной по абсолютной величине оставшемуся расстоянию. Это тоже удобно. При выполнении полета S, оставаясь отрицательной, увеличивается, то есть уменьшается по абсолютной величине. Момент, когда S станет равна нулю, будет соответствовать пролету ППМ.

Существуют такие автоматизированные навигационные системы, выдающие экипажу S и Z, в которых сам экипаж может выбрать, каким вариантом расположения начала системы частноортодромических координат будет пользоваться. Но большинство современных ВС оборудовано системами, в которых однозначно предусмотрен второй из рассмотренных вариантов.

3. Полярная система координат.

Полярные координаты объекта (самолета, радиостанции, ориентира и т.д.) определяются относительно какой-либо заранее оговоренной или подразумеваемой точки (как бы полюса этой системы координат). Этой точкой обычно бывает радиомаяк или самолет. Разумеется, нельзя говорить о полярных координатах радиомаяка относительно самого радиомаяка или о координатах самолета относительно самого себя. Поэтому, когда говорят о полярных координатах ВС, начало координат подразумевается в другой точке (обычно, радиомаяке), и наоборот, полярные координаты радиомаяка могут быть указаны относительно самолета.

Координатами в полярной системе являются пеленг (bearing) и дальность (distance) (рис.2.16).

Рис. 2.16. Полярная система координат

Дальность – расстояние от начала системы координат до объекта (точки). Различают дальность наклонную L (или НД), измеренную по прямой от радиомаяка до рассматриваемой точки (например, до ПМС), и горизонтальную D (или ГД) от радиомаяка до точки на земной поверхности под самолетом, то есть до МС (рис.2.17). Наклонная дальность всегда больше горизонтальной, а совпадает с ней, когда рассматриваемая точка (например, самолет) находится на поверхности земли. Наклонная дальность непосредственно измеряется радионавигационными системами. Горизонтальная дальность используется для определения МС на карте.

Рис. 2.17. Наклонная и горизонтальная дальности

Пеленг (П) – угол в горизонтальной плоскости между направлением, принятым за начало отсчета, и направлением на объект. Отсчитывается по часовой стрелке и измеряется от 0˚ до 360˚. Если объект находится к северу, его пеленг 0˚, если к востоку – 90˚, к югу 180˚, а к западу 270˚.

Часто вместо специфического навигационного термина «пеленг» используется общепринятый (например, в географии) термин «азимут». Это одно и то же.

СИСТЕМЫ КООРДИНАТ И КООРДИНАТНЫЕ ПРЕОБРАЗОВАНИЯ ДЛЯ ЗАДАЧ АЭРОНАВИГАЦИИ | Скрыпник

1. Скрыпник О.Н. Радионавигационные системы воздушных судов: учебник. М.: ИНФРА-М, 2014. 248 с.

2. Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). М.: Наука, 1974. 832 с.

4. Радионавигационный план Российской Федерации. Утвержден приказом Минпромторга России от 28 июня 2015 г. № 2123. 142 с. [Электронный ресурс]. URL: http://docs.cntd.ru/document/4560343228 (дата обращения 03.02.2017).

5. Постановление Правительства Российской Федерации от 28.12.2012 № 1463. О единых государственных системах координат [Электронный ресурс]. URL: http://gis-lab.info/docs/law/statecoord-2012.doc (дата обращения 3.02.2017).

6. Doc 9674 AN/946. World Geodetic System – 1984 (WGS-84) Manual. International Civil Aviation Organization, Second Edition, 2002, р. 134.

7. Moritz. H. Geodetic Reference System 1980 [Электронный ресурс]. URL: http://geodeticscience.org/course/refpapers/00740128.pdf (дата обращения 3.02.2017).

8. ITRF 2008. URL: http://itrf.ensg.ign.fr/ITRF_solutions/2008/ (дата обращения 26.02.2017).

10. 2014 Federal Radionavigation Plan. [Электронный ресурс]. National Technical Information Service, Springfield, Virginia 22161 DOT-VNTSC-OST-R-15-0 URL: https://www.navcen.uscg.gov/ pdf/Federal RadionavigationPlan2014.pdf (дата обращения 3.02.2017).

Локсодромия и Ортодромия. Разница. Сравнение.

Локсодромией, или кривой равных путевых углов, называется линия, пересекающая меридианы под одинаковыми углами.), и значение широты, при которой увеличение пути максимально.

Полеты по локсодромии в настоящее время, особенно на самолетах с ГТД, практического применения не имеют, а поэтому прокладка локсодромии на полетной карте здесь не разбирается. Следует лишь отметить, что локсодромию большой протяженности следует прокладывать по точкам. Для этого необходимо предварительно рассчитать путевой угол и координаты ее промежуточных точек. Элементы локсодромии можно рассчитать по формулам или определить графически при помощи картографической сетки в меркаторской проекции.

Задаваясь долготой промежуточной точки, находят величину D, являющуюся функцией широты. Широту ф промежуточной точки находят по D при помощи специальных таблиц, прилагаемых к учебникам авиационной картографии.

Ортодромией называется линия кратчайшего расстояния между двумя точками на земной поверхности.), и значение широты, при которой увеличение пути максимально.

Ортодромией называется линия кратчайшего расстояния между двумя точками на земной поверхности. Ортодромия является дугой большого круга, плоскость которого проходит через центр земного шара и две заданные точки на поверхности земного шара. Меридианы являются ортодромиями, соединяющими северный и южный географические полюса, — это частные случаи ортодромии. В общем случае ортодромия пересекает меридианы под различными, неравными между собой углами.

Опорный меридиан (ОМ) — меридиан, проходящий через начальную точку ортодромии участка. Расчеты или измерения ортодромического направления полета самолета выполняют от опорного меридиана.

Ортодромическнй путевой угол — угол, образованный северным направлением опорного меридиана и линией заданного пути.

Начальный азимут ортодромии (А) — угол, образованный северным направлением меридиана, проходящего через начальную точку ортодромии, и ортодромией.

При полете по ортодромии следует помнить, что ИПУ ортодромии изменяется на угол б — угол схождения меридианов, который можно вычислить по приближенной формуле

Элементы ортодромии (длина, координаты промежуточных точек и ортодромическнй путевой угол) могут быть вычислены по формулам сферической тригонометрии или графически.

3-й способ. ОПУ может быть измерен непосредственно на карте от любого меридиана с последующим внесением поправки на угол сближения опорного меридиана и меридиана места измерения углов.

Для выполнения полета по ЛЗП в обратном направлении замер ортодромических путевых углов происходит от меридианов, бывших конечными при полете в первоначальном направлении. Следовательно, путевые углы при полете туда и обратно будут отличны друг от друга не только на 180°, но и на величину поправки на сближение меридианов.

Если весь маршрут полета проходит по ортодромии и не имеет ПГ1М, то расчет путевых углов значительно упрощается:

1) маршрут разбивают на участки по 1 000—1200 км.
2) меридианы начальных точек участков считают опорными для обоих направлений и от них измеряют ортодромические путевые углы.

Изображение ортодромии на картах в различных проекциях. На картах, составленных в равноугольной цилиндрической проекции (проекции Меркатора), ортодромия изображается в виде сложной кривой, всегда обращенной выпуклостью к географическим полюсам.

На картах центральной проекции все ортодромии изображаются прямой линией.

На картах в полярной стереографической проекции ортодромия в общем случае изображается дугой окружности. Кривизна ортодромии тем меньше, чем ближе она расположена к географическому полюсу. Меридианы, являющиеся частным случаем ортодромии, на картах полярной стереографической проекции изображаются прямыми линиями.

На бортовой аэронавигационной карте масштаба 1 : 2 000 000, составленной в видоизмененной поликонической проекции, ортодромия в пределах одного листа практически представляет собой прямую линию.

Линией равных азимутов (ЛРА), или равных радиопеленгов, называется линия, в каждой точке которой наземная радиостанция пеленгуется под одним и тем же углом (ЙПР). При помощи линии равных азимутов как линии положения определяют место самолета по наземным импульсным маякам при помощи бортового радиолокатора Линия равных азимутов — сложная кривая. На земном шаре она пересекает меридианы под различными углами и лишь с меридианом, проходящим через точку установки радиостанции, она составляет угол, равный истинному пеленгу радиостанции (ИПР).

(ЛРР) называется линия на земной поверхности, все точки которой находятся от некоторой определенной точки на одинаковом удалении — на окружности малого круга земного шара. Как линия положения, линия равных расстояний в самолетовождении применяется при астрономических измерениях высоты светила с помощью секстанта. В авиационной астрономии ЛРА носит название круга равных высот, на карте она заменяется касательной — прямой равных высот. Элементы этой линии рассчитывают при помощи специальных таблиц высот и азимутов светил — ТВА.

ЛРР используют при применении угломерно-дальномерных и двухполюсных дальномерных радиотехнических систем.

На картах разных проекций ЛРР имеют различный вид. На картах стереографической проекции ЛРР — окружности.

ЛРР наносят на карты с большой степенью точности по промежуточным точкам ЛРР, вычисленным по формулам прямой и обратной геодезических задач (расчеты производятся на поверхности эллипсоида Красовского).

Гиперболой (сферической), или линией равных разностей расстояний, является кривая, в каждой точке которой разность расстояний до двух фиксированных точек (радиостанций) есть величина постоянная. Для целей самолетовождения с использованием линий равных разностей расстояний существуют гиперболические системы навигации. Такие системы включают в себя две пары (или цепочку) наземных станций и бортовое оборудование (приемо-индикаторы), позволяющие с достаточной точностью измерить разность расстояний от самолета до радиостанций.

Место самолета по гиперболической системе определяют пересечением двух гипербол.

Карта — условное уменьшенное обобщенное, построенное по определенным математическим правилам изображение земной поверхности на плоскости.

План — изображение на плоскости в крупном масштабе небольших участков земной поверхности, принимаемых за плоскость.

Картографическая проекция — способ изображения поверхности земного шара или земного эллипсоида на плоскости.

Масштаб — отношение длины линии на карте к длине соответствующей линии на поверхности Земли.

Главный масштаб (М) показывает, во сколько раз уменьшен земной шар (или эллипсоид) при проектировании его на плоскость. Главный масштаб всегда указывается на карте.

Частный масштаб (ц) определяется как отношение бесконечно малого отрезка на карте в данной точке и по данному направлению к соответствующему бесконечно малому отрезку на поверхности земного шара (или эллипсоида).

Частный масштаб в направлении меридиана обозначается буквой т, а в направлении параллели — буквой п.

Главными направлениями называются направления, по которым частные масштабы или минимальны, пли максимальны. Максимальный и минимальный масштабы в данной точке обозначаются а и б. Почти во всех проекциях карт, применяемых в самолетовождении, главные направления совпадают с меридианами и параллелями.

Увеличение масштаба с определяется отношением частного масштаба к главному

Искажение длин У определяется разностью между увеличением масштаба и единицей.

Искажение направлений со определяется разностью между направлением на земном шаре и тем же направлением на карте. Максимальное искажение направлений в данной точке вычисляют по формуле

Масштабом площади р называется отношение площади бесконечно малого участка на карте к соответствующей площади на поверхности глобуса, до размера которого уменьшен земной шар перед проектированием его на плоскость. Искажение площадей характеризуется величиной масштаба площади.

По характеру искажения катографические проекции подразделяются на равноугольные, равнопромежуточные, равновеликие и произвольные.

Равноугольные проекции характеризуются тем, что углы и направления на картах, составленных в этих проекциях, изображены без искажений; частные масштабы по главным направлениям равны между собой; бесконечно малые фигуры на карте сохраняют подобие соответствующим фигурам на земном шаре. Эти данные выражаются следующим образом: a — b; ы = 0; р = ab.

Равноугольные проекции позволяют наиболее просто определять направления и поэтому нашли широкое применение при создании авиационных карт, так как для самолетовождения важно точное измерение направления.

Равнопромежуточными называются проекции, в которых частные масштабы во всех точках по одному из главных направлений равны главному масштабу.

Равновеликими называются проекции, в которых площадь изображаемой фигуры равна площади той же фигуры на карте.

Произвольными называются проекции, которые не равноугольны, не равно-промежуточны и не равновелики.

Произвольные проекции имеют практически очень небольшие искажения в направлениях, длинах и площадях и поэтому нашли широкое применение в самолетовождении. Аэронавигационная карта масштаба 1 : 2 000 000 составлена в видоизмененной поликонической проекции, которая является произвольной.

В зависимости от вида нормальной сетки или способа построения картографической сетки проекции карт, используемых в самолетовождении, подразделяются на цилиндрические, конические, пол и конические, азимутальные и др. Нормальной называется такая сетка координатных линий, соответствующих определенной системе координат, которая имеет наиболее простое изображение в дайной проекции. В некоторых проекциях нормальная сетка совпадает с географической сеткой.

Цилиндрические проекции — это проекции, в которых меридианы нормальной сетки изображаются прямыми линиями, параллельными между собой и отстоящими друг от друга на расстояниях, пропорциональных разности соответствующих долгот; параллели изображаются в виде

прямых линий, перпендикулярных меридианам. Такая сетка получается при проектировании сетки меридианов и параллелей глобуса на боковую поверхность цилиндра (касательного или секущего) и развертывания этой поверхности па плоскость.

В зависимости от расположения оси цилиндра относительно оси вращения глобуса цилиндрические проекции делятся на нормальные цилиндрические проекции (ось цилиндра совпадает с осью вращения глобуса), поперечные цилиндрические проекции (ось цилиндра перпендикулярна оси вращения глобуса), косые цилиндрические проекции (угол между осью вращения цилиндра и осью глобуса больше 0 и меньше 90°).

В нормальных цилиндрических проекциях нормальная сетка совпадает с географической сеткой меридианов и параллелей.

Простая цилиндрическая проекция имеет следующие уравнения прямоугольных координат.

Вид географической сетки в простой цилиндрической проекции: меридианы — прямые, параллельные между собой и отстоящие друг от друга на расстояниях, пропорциональных разности Н долгот; параллели — прямые, перпендикулярные меридианам, отстоящие друг от друга на расстояниях, пропорциональных разности широт.

Проекция равнопромежуточна по направлениям меридианов. Все параллели (кроме экватора) искажены. Искажения в направлении параллелей увеличиваются при увеличении широты. На полюсе это искажение максимально, так как точки полюсов изображаются прямыми, длина которых равна длине экватора. Искажения углов и площадей также увеличиваются при увеличении широты. На полюсе искажение углов (2со) достигает 180°, а масштаб площади равен бесконечности.

Около экватора (в полосе ф < ±5°) проекция практически равноугольна, равновелика и равно-промежуточна.

Равноугольная цилиндрическая проекция Меркатора. Уравнения прямоугольных координат точек в равноугольной цилиндрической п роекции.

Вид географической сетки: меридианы изображаются так же, как в простой цилиндрической проекции; параллели — прямые, перпендикулярные меридианам; расстояние между параллелями при увеличении широты увеличивается пропорционально разности меридиональных частей.

Проекция равноугольна. Искажение длин пропорционально секансу широты. Искажение площадей пропорционально квадрату секанса широты.

На картах равноугольной цилиндрической проекции Меркатора локсодромия всегда изображается прямой линией, пересекающей меридианы под постоянным углом. Около экватора в полосе ф < ±5° проекция практически равноугольна, равновелика и равнопромежуточна.

Равноугольная поперечно — цилиндрическая проекция Гаусса получена в результате проектирования эллипсоида на цилиндр, касающийся какого-то меридиана (оси вращения эллипсоида и цилиндра пересекаются под углом 90°).

В данной проекции полоса эллипсоида, ограниченная меридианами, кратными 6°, проектируется на свой цилиндр, в своей системе плоских.

vamvzlet.blogspot.com: Воздушная навигация — Тема №1 Основы воздушной навигации

1. ТЕМА № 1 Основы воздушной навигации.

2. Основы воздушной навигации.

3. Траектория и линия пути

4. Траектория и линия пути

5. Основные требования к аэронавигации.

7. Основные задачи аэронавигации.

10. Классификация технических средств навигации

11. Классификация технических средств навигации

13. Модели земной поверхности.

14. Физическая поверхность Земли

15. геоид и земной эллипсоид

16. Модели земной поверхности.

17. Модели земной поверхности

18. Референц – эллипсоид Красовского

21. Характеристики WGS-84

22. WGS — 84

23. Основные географические точки , линии и круги.

24. Измерение направлений и расстояний на поверхности Земли.

25. Пересчет единиц расстояния.

26. Системы координат на земной поверхности.

27. Прямоугольные системы координат.

28. Прямоугольные системы координат

29. Геодезические координаты.

30. Геодезические координаты

31. Геодезическая высота.

32. Сферические координаты

33. Сферические координаты

34. Определение широты и долготы по карте.

35. ТЕМА № 1 Основы воздушной навигации

36. Азимут (пеленг) ориентира.

37. Заданный путевой угол и линия заданного пути.

39. Линия пути и линия положения.

40. Ортодромия.

41. Ортодромия.

42. Основные свойства ортодромии.

43. Локсодромия

44. Локсодромия

45. Основные свойства локсодромии.

46. Линия равных азимутов.

47. Линии положения.

49. Географические координаты.

50. Географическая широта.

51. Географическая долгота.

52. ТЕМА № 1 Основы воздушной навигации

53. Системы координат применяемые в навигации.

54. Сферическая система координан

55. Сферическая широта.

56. Сферическая долгота.

57. Геодезическая система координат.

58. Ортодромическая система координат.

59. Общая ортодромическая система координат.

60. Общая ортодромическая система координат.

61. Частная ортодромическая система координат.

62. Прямоугольная система координат.

63. Полярная система координат.

64. Значение наклонной и горизонтальной дальностей

(PDF) Приближенные модели ортодромной навигации

Рисунок 7: Приближение ортодромной навигации по касательному методу

Источник: Сделано авторами

5 ЗАКЛЮЧЕНИЕ

С теоретической точки зрения навигация по

невозможна по большому кругу. Ортодромная навигация

является самой короткой, в то время как локсодромия приемлема

для мореплавания, учитывая, что навигация здесь достигается

с постоянным общим локсодромным курсом (с более длинным пройденным расстоянием

) [Bowditch, 1984].Используя комбинацию этих навигационных кривых

, задача

решается таким образом, чтобы максимально использовать возможности дрома орто-

как кратчайшего расстояния между двумя точками на Земле

. Предлагаемая цель навигации

, таким образом, выполняется с практической точки зрения

, учитывая, что большой круг разделен на единицы

значений конкретных элементов, в зависимости от используемого метода

, по которому затем осуществляется навигация. переносили

локсодромными курсами и локсодромными дистанциями

соответственно.

В статье разработаны три аппроксимационные модели ортодромного движения nav-

. Первая модель

определяет ортодромные промежутки,

, которые могут быть рассчитаны из ортодромической вершины

или начальной позиции, в зависимости от позиции

вершины, находится ли она внутри позиции

вылета и прибытия. или нет. С помощью этого метода корабль

плывет через неравные интервалы расстояний.Вторая модель

предполагает разделение ортодромии на единицы

интервалов расстояний с величиной 0,5º

30 м.

Таким образом, определяются координаты ортодромного взаимного расположения

, и судно плывет в постоянных локсо-

курс дромов между ними. Этот метод

является наиболее точным из всех трех разработанных. В третьем методе

ортодромная навигация приблизительно

имитируется путем определения изменений курса ΔK ортодромической единицы

.Здесь сначала необходимо

вычислить изменения курса единицы, после чего определяются единицы

Ортодромные расстояния

, выраженные в нау-

тикальных милях, представляющих навигацию судна

в определенном курсе, в некотором смысле. что появится требуемая аль-

терация ΔK.

Степень, в которой навигация будет ортогональной,

дром — подобная, зависит от нескольких параметров —

с учетом конкретного случая навигации и с учетом курсов навигационной системы

и расстояний между двумя позициями

.В плавании по экватору и меридиану

ортодромия и локсодромия перекрываются — их расстояния

равны. Это также относится к меньшим расстояниям между позициями, где нет расхождений между этими кривыми. Однако в некоторых случаях разница между этими двумя расстояниями

достигает заметных значений, и затем, приблизившись к ортодрому, можно значительно сократить время, затрачиваемое на навигацию

БЛАГОДАРНОСТИ

Авторы выражают признательность за поддержку проекта

«Исследование корреляций элементов морского транспорта в морском движении» (112-1121722-

3066), финансируемого Министерством науки и образования.

и Спорт Республики Хорватия.

ССЫЛКИ

[1] Бенкович, Ф. И другие: Terestrička i elektronska navi-

gacija, Hidrografski institut JRM, Сплит, 1986.

[2] Bowditch, N .: The American Practical Navigator, Vol I,

US Defense Mapping Agency, Bethesda, 1984.

[3] Kos, S .: Aproksimacija plovidbe po ortodromi, Zbornik ra-

dova Pomorskog fakulteta, Rijeka, 1996.

[4] Kos, S., Zorović, D., Vranić D .: Terestrička i elektronička

navigacija, Pomorski fakultet u Rijeci, Rijeka, 2010.

n [KCC] : On Loxodromic Navigation, The Journal

of Navigation, Королевский институт навигации, 45, мост Cam-

, 1992.

[5] Зорович, Д. И другие: Vademecum Maritimus, Pomorski

fakultet u Rijeci, Rijeka, 2002.

Онлайн-калькулятор: Расстояние через Землю

Если вы хотите измерить расстояние от одной точки на Земле к другому вы должны использовать формулу большого круга или ортодромного расстояния. Для этого у нас даже есть два калькулятора: один использует формулу гаверсинуса, а другой — формулу Винсенти.

Однако что, если вы хотите знать расстояние между двумя точками на Земле через Землю, а не через поверхность? Как оказалось, проблема относительно проста, за исключением пары подводных камней.Калькулятор ниже находит расстояние между двумя точками на Земле, а вывод формулы со всеми ошибками можно найти под калькулятором.

Расстояние по Земле

Точность вычисления

Цифры после десятичной точки: 3

content_copy Ссылка сохранить Сохранить расширение Виджет

Расстояние сквозь Землю

Хорошо, у нас есть две точки на поверхности Земли, определяемые их широтой и долготой, и мы хотим знать расстояние между ними, проходя «сквозь» Землю, а не вокруг нее.Технически у нас есть сферические координаты каждой точки в трехмерном пространстве, потому что мы знаем радиус Земли, угол наклона (широту) и азимутальный угол (долготу). Если мы преобразуем их в декартовы координаты с x, y, z в трехмерном пространстве, мы можем легко найти расстояние, используя известную формулу евклидова расстояния:

Итак, давайте определим нашу декартову систему координат. Исток будет центром Земли. Ось x будет указывать на пересечение нулевого меридиана с плоскостью экватора.Ось y будет указывать на 90 градусов западного пересечения меридиана с плоскостью экватора, ось z будет указывать на север.

Декартова система координат

— это наша долгота, это наша широта.

Декартовы координаты могут быть получены из сферических координат с помощью следующих соотношений:

Мы почти закончили, но нам все еще нужно учесть пару факторов, которые возникают из-за того, что в геодезии Земля аппроксимируется сплюснутым сфероидом или эллипсоидом вращения.Итак, когда мы говорим о координатах, мы говорим о координатах на поверхности опорного эллипсоида, используемого в геодезической системе координат, в данном случае WGS 84 (следовательно, расстояние также измеряется между двумя точками опорного эллипсоида). Факторы:

Поскольку Земля сплющена на полюсах и выпуклая на экваторе, радиус Земли непостоянен и зависит от широты точки. Таким образом, нам нужно вычислить его для обеих точек, что можно сделать с помощью этого калькулятора.

WGS 84 Широта точки — это геодезическая широта, определяемая углом между плоскостью экватора и нормалью к эллипсоиду вместо геоцентрической широты, которая определяется углом между плоскостью экватора и линией, соединяющей точку с центром эллипсоида. .Поскольку источником нашей декартовой системы является центр Земли, нам необходимо преобразовать геодезическую широту в геоцентрическую широту для обеих точек.

Мы учитываем те, которые используют эти формулы:
,
где — геоцентрическая широта, — геодезическая широта, — большая полуось эллипсоида, — малая полуось эллипсоида.

Подводя итог, чтобы рассчитать расстояние, мы должны сделать следующее:

Вычислить радиус Земли в каждой точке
Вычислить геоцентрическую широту в каждой точке
Преобразует сферические координаты каждой точки в декартовы координаты из вычисленного радиуса, геоцентрической широты и долготы в x, y, z.
Вычислить расстояние по формуле Евклидова расстояния

Расстояние по дуге большого круга | Тригонометрия: составные углы

Как найти формулу для расстояния по большому кругу?

В «Потерянном, но прекрасном: гаверсинус» мы исследовали расстояния по большим кругам на Земле и посмотрели на формулу гаверсинуса для их вычисления: \ [\ mathop {\ mathrm {haversin}} \ left (\ frac {d} {R} \ right ) = \ mathop {\ mathrm {haversin}} (\ phi_2- \ phi_1) + \ cos {\ phi_1} \ cos {\ phi_2} \ mathop {\ mathrm {haversin}} (\ lambda_2- \ lambda_1).2 {\ left (\ frac {\ lambda_2- \ lambda_1} {2} \ right)}. \]

В этой статье мы исследуем, откуда взялась эта формула, и почему навигаторы могли использовать в своих вычислениях незнакомый гаверсинус, а не обычные синусы и косинусы.

Предварительные мероприятия

При расчетах мы можем использовать любые единицы измерения расстояния, которые захотим: изменение единиц не влияет на значение \ (\ frac {d} {R} \) (до тех пор, пока мы используем одни и те же единицы для обоих \ (d \) и \ (R \)). Наиболее удобно, мы можем выбрать единицы измерения так, чтобы радиус Земли был равен \ (R = 1 \), что означает, что мы работаем с сферой единиц .2 {\ left (\ frac {\ lambda_2- \ lambda_1} {2} \ right)}, \ конец {уравнение} \]

, который выглядит немного проще. Мы будем работать с этими формами повсюду.

Расстояние по большому кругу, \ (d \), — это более короткая дуга, соединяющая две точки на большом круге. Мы также можем рассмотреть хорду (прямую), соединяющую две точки, и пусть ее длина равна \ (C \).

Мы можем сразу заметить некоторые отношения между \ (d \), \ (C \) и углом \ (\ sigma \) (измеренным в радианах), который дуга большого круга образует с центром сферы: мы имеем \ ( d = \ sigma \) (так как радиус равен \ (1 \)), и, нарисовав равнобедренный треугольник \ (POQ \), мы видим, что \ (C = 2 \ sin \ bigr (\ frac {\ sigma} { 2} \ bigr) \):

Объединяя их, удаляя \ (\ sigma \), \ [\ frac {C} {2} = \ sin \ left (\ frac {d} {2} \ right).2 \ left (\ frac {d} {2} \ right) = 4 \ mathop {\ mathrm {haversin}} d. \ конец {уравнение} \]

Теперь мы предлагаем четыре подхода к выводу формулы гаверсинуса. Первые два из них используют координаты, поэтому мы начнем с этого.

Координаты

Учитывая точку на единичной сфере с широтой \ (\ phi \) и долготой \ (\ lambda \), мы можем вычислить соответствующие декартовы координаты, как показано на следующей диаграмме.

Каковы декартовы координаты \ (P \) (то есть его координаты \ ((x, y, z) \))?

Проверьте свой ответ

Из диаграммы видно, что

\ [\ begin {align *} & \ text {сначала} & z & = \ sin \ phi \\ & \ text {и} & OP ‘& = \ cos \ phi, \\ & \ text {so} & x & = \ cos \ phi \ cos \ lambda \\ & \ текст {и} & y & = \ cos \ phi \ sin \ lambda.\ конец {выравнивание *} \]

Как только мы узнаем декартовы координаты точек \ (P \) и \ (Q \) с широтами \ (\ phi_1 \) и \ (\ phi_2 \) и долготами \ (\ lambda_1 \) и \ (\ lambda_2 \ ) соответственно, мы можем вычислить разницу в координатах \ (x \), \ (y \) и \ (z \) двух точек и использовать их для вычисления соответствующих расстояний или углов, чтобы найти \ (d \) .

Однако выражения станут довольно громоздкими с таким количеством переменных, поэтому мы ищем способ упростить вещи, прежде чем идти дальше.

Одна уловка состоит в том, чтобы заметить, что расстояния и угол \ (\ sigma \) остаются неизменными, если мы вращаем сферу вокруг оси север-юг. Это изменяет только долготу точек, поэтому мы можем вращать его до тех пор, пока \ (P \) не будет иметь долготу \ (0 \), а \ (Q \) не будет иметь долготу \ (\ lambda_2- \ lambda_1 \), что мы будем называть \ (\ Delta \ lambda \) (разница между \ (\ lambda \) s).

Тогда координаты \ (P \) и \ (Q \) станут: \ [\ begin {align *} P & = (\ cos \ phi_1, 0, \ sin \ phi_1) \\ Q & = (\ cos \ phi_2 \ cos (\ Delta \ lambda), \ cos \ phi_2 \ sin (\ Delta \ lambda), \ sin \ phi_2).2 \ bigl (\ tfrac {d} {2} \ bigr) = \ tfrac {1} {2} \ bigl (1- \ cos \ phi_1 \ cos \ phi_2 \ cos (\ Delta \ lambda) — \ sin \ phi_1 \ sin \ phi_2 \ bigr). \]

Затем мы можем продолжить точно так же, как в подходе 1.

Подход 3: сферическая тригонометрия

Подобно тому, как существуют правила синуса и косинуса для треугольников на плоскости, существуют аналогичные правила для треугольников на сфере.

Вот рисунок сферического треугольника:

Углы \ (A \), \ (B \) и \ (C \) — это углы в вершинах \ (A \), \ (B \) и \ (C \) треугольника, а \ ( a \), \ (b \) и \ (c \) — стандартные длины сторон.Но если мы возьмем сферу радиусом \ (1 \), то их также можно рассматривать как углы: например, \ (a \) — это угол \ (\ angle BOC \). Поэтому мы предполагаем, что с этого момента сфера имеет радиус \ (1 \).

Есть два правила сферического косинуса и одно правило сферического синуса, а именно:

Правило сферического косинуса (1): \ [\ cos a = \ cos b \ cos c + \ sin b \ sin c \ cos A \] (и аналогичные уравнения с \ (a \), \ (b \), \ (c \) и \ (A \), \ (B \), \ (C \) переставлены)
Правило сферического косинуса (2): \ [\ cos A = — \ cos B \ cos C + \ sin B \ sin C \ cos a \] (и аналогичные уравнения с \ (a \), \ (b \), \ (c \) и \ (A \), \ (B \), \ (C \) переставлены)
правило сферического синуса: \ [\ dfrac {\ sin A} {\ sin a} = \ dfrac {\ sin B} {\ sin b} = \ dfrac {\ sin C} {\ sin c} \]

Можете ли вы использовать эту информацию, чтобы найти выражение для \ (\ cos \ sigma \), а затем для \ (\ sin ^ 2 \ bigl (\ frac {d} {2} \ bigr) \) в нашем случае?

Проверьте свой ответ

Если мы возьмем \ (A \) за северный полюс, \ (B \) за нашу точку \ (P \) и \ (C \) за нашу точку \ (Q \), то \ (a = \ sigma \), \ (b = \ frac {\ pi} {2} — \ phi_2 \) (иногда называемый широтой для \ (Q \) — вы понимаете, почему?), \ (c = \ frac {\ pi} {2} — \ phi_1 \) и \ (A = \ Delta \ lambda \). 2 \ bigl (\ tfrac {d} {2} \ bigr) = \ tfrac {1} {2} \ bigl (1- \ cos \ phi_1 \ cos \ phi_2 \ cos (\ Delta \ lambda) — \ sin \ phi_1 \ sin \ phi_2 \ bigr).2 = 4 \ mathop {\ mathrm {haversin}} d, \] где \ (d \) — это расстояние по большому кругу (или угол между ними), а \ (C \) — соответствующая длина хорды.

Мы хотим найти расстояние по большому кругу \ (d \) между точками \ (P \) и \ (Q \) с широтой \ (\ phi_1 \) и \ (\ phi_2 \) и долготой \ (\ lambda_1 \) и \ (\ lambda_2 \) соответственно.

Подумав о симметрии, нам предлагается также рассмотреть точки \ (R \) и \ (S \) с широтами \ (\ phi_1 \) и \ (\ phi_2 \), но с измененными долготами \ (\ lambda_2 \) и \ (\ lambda_1 \) соответственно.Это дает нам следующую конфигурацию:

На этой диаграмме синие линии — это прямые хорды (хотя оптическая иллюзия заставляет это выглядеть иначе), а красная линия — это большой круг между \ (P \) и \ (Q \).

Можете ли вы использовать эту диаграмму для вывода формулы гаверсинуса?

Проверьте свой ответ

Первое, что нужно заметить, это то, что прямые \ (PR \) и \ (SQ \) параллельны. 2 + ab.2 \), \ (a \) и \ (b \), поэтому их замена дает \ [4 \ mathop {\ mathrm {haversin}} d = 4 \ mathop {\ mathrm {haversin}} (\ phi_2- \ phi_1) + 4 \ cos \ phi_1 \ cos \ phi_2 \ mathop {\ mathrm {haversin}} (\ lambda_2- \ lambda_1). \] После деления на \ (4 \) получается формула гаверсинуса.

Как соотносятся эти четыре подхода?

Зачем нужны гаверсины?

Конечно, мы могли бы просто использовать \ (\ cos \ bigl (\ frac {d} {R} \ bigr) = \ cos \ phi_1 \ cos \ phi_2 \ cos (\ Delta \ lambda) + \ sin \ phi_1 \ sin \ phi_2 \) для вычисления расстояний по большому кругу, как мы нашли в подходах 2 и 3? Зачем кому-то хаверсин? (Мы повторно ввели сюда радиус \ (R \), поскольку в практических расчетах будут использоваться стандартные единицы измерения.{-5} \ конец {выравнивание *} \]

Используя эти значения, вычислите расстояние по большому кругу от Кале до Дувра, используя две разные формулы (и вы можете использовать калькулятор для умножения и вычисления конечных обратных косинусов и гаверсинусов). Чтобы по-настоящему подражать прошлому, округлите все свои промежуточные вычисления до 4 значащих цифр.

Наши расчеты

По формуле \ [\ cos \ left (\ frac {d} {R} \ right) = \ cos \ phi_1 \ cos \ phi_2 \ cos (\ Delta \ lambda) + \ sin \ phi_1 \ sin \ phi_2 \] мы можем вычислить следующим образом (до 4 значащих цифр):

\ [\ begin {align *} \ cos \ phi_1 \ cos \ phi_2 & = 0.6273 \ раз 0,6297 = 0,3950 \ \ cos \ phi_1 \ cos \ phi_2 \ cos (\ Delta \ lambda) & = 0,3950 \ times1.0000 = 0,3950 \\ \ sin \ phi_1 \ sin \ phi_2 & = 0,7788 \ times0,7768 = 0,6050 \\ \ cos \ left (\ frac {d} {R} \ right) & = 0,3950 + 0,6050 = 1,0000 \\ \ frac {d} {R} & = 0 \\ d & = 0 \ конец {выравнивание *} \]

Это весьма прискорбно: мы потеряли слишком много информации, потому что \ (\ cos (\ Delta \ lambda) \) так близко к \ (1 \). Фактически, это \ (0,9999588 \) с точностью до 7 знаков после запятой, но даже эта повышенная точность не поможет, если мы продолжим работать с 4 знаками после запятой.Таблицы не были доступны с таким уровнем точности, поэтому эта формула бесполезна для расчета коротких расстояний.

С другой стороны, формула гаверсинуса \ [\ mathop {\ mathrm {haversin}} \ left (\ frac {d} {R} \ right) = \ mathop {\ mathrm {haversin}} (\ phi_2- \ phi_1) + \ cos {\ phi_1} \ cos {\ phi_2} \ mathop {\ mathrm {haversin}} (\ lambda_2- \ lambda_1). \] Таким образом, мы можем вычислить \ (d \) (помня в конце, что мы нужно работать в радианах, принимая обратный гаверсинус):

\ [\ begin {align *} \ mathop {\ mathrm {haversin}} (\ phi_2- \ phi_1) & = \ mathop {\ mathrm {haversin}} 0.\ circ \); они должны быть более точными, чтобы дать более точный ответ.

Причина, по которой простая формула не работает для малых расстояний, заключается в том, что если \ (\ Delta \ lambda \) мало, то \ (\ cos (\ Delta \ lambda) \) почти точно равно \ (1 \). Тогда формула становится \ [\ cos \ left (\ frac {d} {R} \ right) \ приблизительно \ cos \ phi_1 \ cos \ phi_2 + \ sin \ phi_1 \ sin \ phi_2 = \ cos (\ phi_2- \ phi_1) . \] Если разница в широтах \ (\ phi_2- \ phi_1 \) также мала, то это дает \ (\ cos \ bigl (\ frac {d} {R} \ bigr) \ приблизительно1 \), и так что \ (\ frac {d} {R} \ ок0 \).

Вместо этого формула гаверсинуса работает в терминах синусов разницы между широтой и долготой. Если \ (\ Delta \ lambda \) мало, то \ (\ sin (\ Delta \ lambda) \ приблизительно \ Delta \ lambda \) (пока мы работаем в радианах), поэтому работа с 4 значащими цифрами все равно будет быть очень точным.

Geodesy: как рассчитать расстояние по прямой между двумя точками, которое представлено долготой и широтой? — Использование

Вот перевод на Юлию кода Matlab, который я написал много лет назад.Это приблизительно в том смысле, что предполагается сферическая модель Земли, но я счел ее полностью подходящей для построения графиков.

  с использованием LinearAlgebra: ⋅, norm, ×

"" "
    gcinterp (p1, p2, dθ)

Вычислите список точек на интерполяции большого круга, предполагая сферическую модель земли.

### Входные аргументы

- `p1`,` p2`: Итерации длины 2, содержащие долготу λ и широту L
               в градусах начальной и конечной точек искомой дуги.

- `dθ`: желаемое угловое приращение в градусах для расстояния между точками вдоль
        интерполированная дуга большого круга.### Возвращаемое значение
Вектор упорядоченных пар `(λᵢ, Lᵢ)` (долготы и широты в градусах)
указывает на траекторию большого круга, соединяющую `p1` и` p2`. Расстояние между длиной дуги
точки будут равны или немного меньше, чем `dθ`.
"" "
функция gcinterp (p1, p2, dθ)
    λ₁, L₁ = с плавающей запятой (p1 [1: 2])
    λ₂, L₂ = с плавающей запятой (p2 [1: 2])
    rg1 = ll2rect (λ₁, L₁)
    rg2 = ll2rect (λ₂, L₂)
    ct0 = rg1 ⋅ rg2
    st0 = норма (rg1 × rg2)
    rg1 / = st0
    rg2 / = st0
    θ0 = atand (st0, ct0) # длина дуги большого круга
    п = 1 + ceil (Int, θ0 / dθ)
    points = [(λ₁, L₁) для _ в 1: n]
    for (i, θ) в перечислении (диапазон (0, θ0, length = n))
        rvec = rg1 * sind (θ0-θ) + rg2 * sind (θ)
        точки [i] = rect2ll (rvec)
    конец
    points [1] = p1 [1], p1 [2] # Устранение ошибок округления
    баллы [n] = p2 [1], p2 [2]
    точки
конец

"" "
    ll2rect (λ, L)

Преобразуйте долготу `λ` и широту` L` (обе в градусах) в 3-вектор прямоугольных координат."" "
функция ll2rect (λ, L)
    sinλ, cosλ = sincosd (λ)
    sinL, cosL = sincosd (L)
    [cosL * cosλ, cosL * sinλ, sinL]
конец

"" "
    rect2ll (rvec)

Преобразуйте прямоугольные координаты (3-вектор единичной длины) в кортеж (долгота, широта).
Угловые единицы на выходе - градусы.
"" "
функция rect2ll (rvec)
    λ = atand (rvec [2], rvec [1])
    L = asind (rvec [3])
    (λ, L)
конец

Надеюсь, это поможет.

Как разрабатывать функции с географией | Надим Кавва

Пример теории и науки о реальных данных

Фото Марьян Блан | @marjanblan на Unsplash

У каждой компании, продающей товары или услуги, есть физический адрес.Нет сомнений в том, что местоположение может сделать или разрушить бизнес. Для специалистов по обработке данных извлечение геодезических характеристик, связанных с геометрической формой Земли, может дать четкое представление и значительно повысить производительность моделей машинного обучения.

В этой статье мы собираемся использовать набор данных Yelp, в частности файл business.json , для извлечения функций, зависящих от местоположения.

Мы также будем использовать Справочник по математике Бронштейна, Семендяева, Мусиола, Мюлига (ссылка на PDF) и соответствующее резюме Яна Филипа Матушека

Документация Yelp дает хороший обзор функций, ниже — краткий фрагмент .

{
// строка, уникальная строка из 22 символов, идентификатор предприятия
"business_id": "tnhfDv5Il8EaGSXZGiuQGg",

// строка, название компании
"name": "Garaje",

// строка, полный адрес предприятия
«адрес»: «475 3rd St»,

// строка, город
«city»: «San Francisco»,

// строка, 2-символьный код штата, если применимо
"state": "CA",

// строка, почтовый индекс
"postal code": "94107",

// float, широта
"latitude": 37.7817529521,

// число с плавающей запятой, долгота
"долгота": -122.39612197,

// число с плавающей запятой, рейтинг в звездочках, округлено до полузвезды
"звездочки": 4,5,

// целое число, число отзывов
"review_count": 1198

Некоторые области, как правило, очень развиты и имеют много предприятий. Кроме того, похожие предприятия, как правило, группируются близко друг к другу.

Например, предприятие, указанное выше, находится в районе Сан-Франциско SoMA (, где продается отличный гуакамоле ), и вокруг него сосредоточено множество других ресторанов.

Мы будем использовать широту и долготу, чтобы запросить фрейм данных для предприятий вокруг него. Для этого нам нужно освежить память о географии.

Земля представляет собой несовершенную сферу с приблизительным радиусом 6357 километров. Географическая система координат — это метод, который позволяет размещать точки на сферах и часто используется при землеустройстве среди других профессий.

Мы определяем широту как угол от нуля градусов на экваторе до 90 градусов на полюсах.И наоборот, долгота проходит от полюса к полюсу и колеблется от 0 до 180 градусов. На рисунке ниже эти две концепции показаны на сфере.

Источник: https://en.wikipedia.org/wiki/Geographic_coordinate_system

Теперь, когда у нас определена наша система координат, нам нужен метод, который определяет ограничивающую рамку вокруг точки интереса и захватывает все точки в ограниченной области вокруг нее. .

Две точки на сфере

В качестве первого подхода мы можем вычислить ортодромное расстояние между двумя точками P (lat1, long1) и Q (lat2, long2) на сфере с радиусом R :

Этот метод чрезмерно медленный, поскольку он означает вычисление расстояния между точкой и всеми остальными для всех точек в наборе данных.

Угловой радиус

Угловой радиус лучше подходит для описания размера сферы или круга с данной точки зрения. Например, если мы хотим покрыть расстояние d на сфере радиуса R , тогда угловой радиус r будет:

Bounding Box

Затем мы определяем узлы, которые полностью охватывают область, захваченную угловым радиусом. . Движение по широте означает, что мы можем двигаться по меридиану, сохраняя фиксированную долготу.Следовательно, ограничивающая широта определяется как:

Перемещение по кругу широты для определения ограничительной долготы не работает таким же образом, как указано выше. На изображении ниже точки T1 и T2 имеют максимальную и минимальную долготу соответственно. Они не находятся на том же круге широты, что и достопримечательность M , но находятся ближе к полюсу.

Источник: Ян Филип Матушек

Широта T1 и T2 составляет:

Следовательно, предельные долготы рассчитываются следующим образом:

Где:

Math to Python

Мы можем интерпретировать приведенную выше методологию в коде Python :

В примере Гараже наш код вернет фрейм данных, в котором перечислены все предприятия в радиусе d_query = 2 км от Гараже, как показано на изображении ниже:

Источник: https: // www.mapdevelopers.com/draw-circle-tool.php

Учитывая фрейм данных, подобный тому, который у нас есть, мы можем написать код, который возвращает копию (примечание : не представление ) географически ограниченного фрейма данных

Что мы можем извлечь из этой информации? Оказывается, мы можем узнать довольно много:

Сколько предприятий находится поблизости ( плотность )
Сравнение ценового диапазона
Сравнение звездных рейтингов
Количество отзывов
и т. Д …

При сравнении это часто бывает хорошей идеей масштабировать функции.Например, при сравнении цен мы можем стандартизировать ( z нормализация ) цену, используя среднее значение и стандартное отклонение запрошенного фрейма данных.

Звездный рейтинг

В качестве первой функции мы можем построить стандартизированный звездный рейтинг каждой записи относительно ее ближайших соседей. Похоже, что это распределение по Гауссу, так что большинство предприятий в одном районе довольно однородны с точки зрения рейтинга.

Диапазон цен

Сравнение цен представляется двухрежимным, более подробный анализ может сделать запрос более строгим и включать только предприятия одного типа.

Подсчет плотности

Мы определяем плотность как количество предприятий в ограниченном прямоугольнике. Для этой функции нет необходимости делать какую-либо стандартизацию.

Обратите внимание, что график ниже будет сильно отличаться в зависимости от радиуса запроса и степени развития в области.

Правильная разработка функций может дать вашей модели машинного обучения преимущество, необходимое для повышения ее производительности. Принимая во внимание географию, мы можем получить характеристики, зависящие от местоположения.

В случае набора данных Yelp AUC для каждой модели улучшилась как минимум на 5% при подключении геодезических функций.Кроме того, они хотя бы раз появлялись в топ-5 самых важных функций по всем алгоритмам!

Поддержка геопространственных данных в средах виртуализации данных

Геопространственные данные и мир виртуализации данных

Геопространственные данные — это информация о физическом объекте, которая может быть представлена набором значений в системе координат. Этот вид данных сегодня очень часто используется для обогащения наборов непространственных данных, в противном случае, полезными представлениями местоположений, размеров или форм, которые могут быть пространственно или географически связаны с ними.Сценарии использования варьируются от геолокации магазинов сети на карте до географической идентификации транспортных линий или энергоресурсов.

Виртуализация данных, как ключевая технология в области интеграции данных, может играть важную роль в управлении и публикации геопространственных данных. Геопространственные данные могут проходить через систему виртуализации данных из источников, в которых они хранятся, могут быть интегрированы с данными из других источников, чтобы предлагать более обширную географически доступную версию последних, или даже могут быть созданы как такие геопространственные данные. на уровне виртуализации данных из значений его компонентов и метаданных, потенциально поступающих из различных и разнородных источников.

Отсюда уровень виртуализации данных может предоставить своим клиентским системам наборы интегрированных геопространственных данных, которые могут удовлетворить их потребности, позволяя им использовать эти данные в различных географических вычислениях или в разнообразных механизмах визуализации.

Проблемы геопространственных данных

Обработка геопространственных данных сопряжена с рядом проблем, наиболее распространенной из которых является повышение сложности, возникающее, когда эти данные необходимо не только отформатировать или изменить, но также вычислить или оперировать каким-либо образом.Многие функции для выполнения вычислений с геопространственными данными уже широко доступны и хорошо документированы, но есть функция, присущая геопространственным данным, которая может значительно усложнить эти вычисления: системы координат (CRS).

Системы координат

(CRS) или Пространственные справочные системы (SRS) определяют картографические проекции и, таким образом, придают истинное географическое значение координатным значениям в геопространственных данных или геометрии. Они необходимы для реального смысла значений, установленных в геометрических координатах, но они добавляют сложности из-за несоответствия возможных проекций карты.Несоответствие, возникающее из-за различных доступных вариантов преобразования наборов 2D-координат в точки на не плоской, но и не сферической поверхности Земли (или другой планеты).

Конечно, существует несколько CRS, каждая из которых основана на разных предположениях, полезных для разных сценариев и с разными ограничениями и уровнями точности. Таким образом, вычисление геопространственных данных может стать трудным, когда данные могут быть выражены с использованием различных CRS или когда мы намерены получить цифры, которые сильно зависят от используемой проекции карты, например, ортодромные расстояния.Нормализация и преобразование в известные системы координат, такие как WGS84 или Универсальный ход Меркатора (UTM), усложняют работу в целом, но в то же время повышают практическую полезность пакета обработки геопространственных данных.

Общие геопространственные функции

Пакет для обработки геопространственных данных может предложить большое количество функций, которые можно сгруппировать в три основные категории:

Создание геометрических данных (обычно в формате Well-Known-Text (WKT) или Well-Known-Binary (WKB)): точки, линии, многоугольники.
Получение компонентов геометрических данных: получение значений координат геометрий, количества измерений, вложенных геометрий (в сложных) и т. Д.
Операция, самая большая и сложная группа, обе возвращающие в результате другие геометрии — например, объединение, пересечение, буфер, кольцо, центроид… — или возвращающие скалярные данные — такие как площадь, длина или ортодромные расстояния.

Кроме того, для правильной работы с данными, потенциально выраженными в различных системах отсчета координат, также потребуются функции, способные преобразовывать геометрию между различными CRS, и / или прозрачно применяться под ними, чтобы нормализовать геометрию к системам отсчета, необходимым для правильного работая с ними.

Взаимодействие с клиентскими приложениями: GeoJSON

Наконец, геопространственные данные, обрабатываемые и / или вычисляемые в системе интеграции данных, такой как платформа виртуализации данных, могут быть предложены ее клиентским приложениям с использованием не только обычных форматов и протоколов, таких как JDBC, ODBC, REST, OData и т. Д., Но также и с использованием стандартного формата GeoJSON (RFC7946), который обеспечивает большую совместимость с существующими системами визуализации карт:

DenodoLabs — это передовая команда Denodo, занимающаяся разработкой программного обеспечения, которая постоянно следит за последними достижениями в области виртуализации данных и создает экосистему компонентов DenodoConnect, которая позволяет клиентам Denodo извлекать максимальную прибыль из своих установок Denodo в таких ключевых областях, как интеграция больших данных и SaaS. подключение, тестирование, управление и многое другое.

Последние сообщения от Denodo Labs (посмотреть все)

оптимальных картографических проекций для анализа маршрутов миграции на большие расстояния в JSTOR

Abstract

Мало внимания уделялось типам карт, используемых в исследованиях миграции. Однако мы думаем, что анализ миграции в двух измерениях с применением различных правил проекции карты может дать ценную информацию о программах биологической борьбы с миграцией на большие расстояния. Земля, будучи глобусом, не может быть спроецирована на двумерную плоскость без искажения одного или нескольких из следующих свойств: расстояние, направление или площадь.Картографические проекции, которые правильно сохраняют два из вышеупомянутых свойств, делают это только с одной точки. Для анализа маршрутов дальних мигрантов расстояние и направление являются наиболее важными факторами из-за высокой стоимости путешествия, будь то энергия или время. Когда на мигрантов не влияют топографические особенности, ожидается, что они будут следовать либо ортодромам, либо локсодромам. Ортодромия (большой круг) — это кратчайший путь между двумя точками на поверхности Земли, локсодромия (круговая линия) — это путь постоянного курса между двумя точками.Обсуждаются и проиллюстрированы свойства нескольких картографических проекций и их полезность для оценки того, в какой степени пути перелетных птиц включают влияние сферической Земли. Для изучения принципов ортодромной ориентации наиболее важны азимутальные проекции, в основном гномонические, орфографические, стереографические и азимутальные эквидистантные проекции. Меркатор и связанные с ним проекции (наклонная проекция Меркатора и локсимутальная проекция) показывают миграцию в свете локсодромов и ориентацию по постоянным географическим или магнитным курсам.

Информация о журнале

Journal of Avian Biology публикует эмпирические и теоретические исследования во всех областях орнитологии с упором на поведенческую экологию и эволюцию. Желательно, чтобы статьи проверяли гипотезы или исследовали новую почву. Чисто описательные исследования принимаются только тогда, когда они содержат важную информацию, которая вызывает новые вопросы или открывает новые возможности.

Информация для издателя

Wiley — глобальный поставщик контента и решений для рабочих процессов с поддержкой контента в областях научных, технических, медицинских и научных исследований; профессиональное развитие; и образование.Наши основные направления деятельности выпускают научные, технические, медицинские и научные журналы, справочники, книги, услуги баз данных и рекламу; профессиональные книги, продукты по подписке, услуги по сертификации и обучению и онлайн-приложения; образовательный контент и услуги, включая интегрированные онлайн-ресурсы для преподавания и обучения для студентов и аспирантов, а также для учащихся на протяжении всей жизни. Основанная в 1807 году компания John Wiley & Sons, Inc. уже более 200 лет является ценным источником информации и понимания, помогая людям во всем мире удовлетворять свои потребности и воплощать в жизнь их чаяния.Wiley опубликовал работы более 450 лауреатов Нобелевской премии во всех категориях: литература, экономика, физиология и медицина, физика, химия и мир. Wiley поддерживает партнерские отношения со многими ведущими мировыми обществами и ежегодно издает более 1500 рецензируемых журналов и более 1500 новых книг в печатном виде и в Интернете, а также базы данных, основные справочные материалы и лабораторные протоколы по предметам STMS. Благодаря растущему предложению открытого доступа, Wiley стремится к максимально широкому распространению и доступу к публикуемому контенту, а также поддерживает все устойчивые модели доступа.Наша онлайн-платформа, Wiley Online Library (wileyonlinelibrary.com), является одной из самых обширных в мире междисциплинарных коллекций онлайн-ресурсов, охватывающих жизнь, здоровье, социальные и физические науки и гуманитарные науки.

Корзина

Системы координат, применяемые в самолетовождении

Ортодромическая система координат.

Системы координат и координатные преобразования для задач аэронавигации Текст научной статьи по специальности «Строительство и архитектура»

Системы координат, применяемые в навигации (сферическая, полярная, ортодромическая)

СИСТЕМЫ КООРДИНАТ И КООРДИНАТНЫЕ ПРЕОБРАЗОВАНИЯ ДЛЯ ЗАДАЧ АЭРОНАВИГАЦИИ | Скрыпник

Локсодромия и Ортодромия. Разница. Сравнение.

Увеличение масштаба с определяется отношением частного масштаба к главному

vamvzlet.blogspot.com: Воздушная навигация — Тема №1 Основы воздушной навигации

1. ТЕМА № 1 Основы воздушной навигации.

2. Основы воздушной навигации.

3. Траектория и линия пути

4. Траектория и линия пути

5. Основные требования к аэронавигации.

7. Основные задачи аэронавигации.

10. Классификация технических средств навигации

11. Классификация технических средств навигации

13. Модели земной поверхности.

14. Физическая поверхность Земли

15. геоид и земной эллипсоид

16. Модели земной поверхности.

17. Модели земной поверхности

18. Референц – эллипсоид Красовского

21. Характеристики WGS-84

22. WGS — 84

23. Основные географические точки , линии и круги.

24. Измерение направлений и расстояний на поверхности Земли.

25. Пересчет единиц расстояния.

26. Системы координат на земной поверхности.

27. Прямоугольные системы координат.

28. Прямоугольные системы координат

29. Геодезические координаты.

30. Геодезические координаты

31. Геодезическая высота.

32. Сферические координаты

33. Сферические координаты

34. Определение широты и долготы по карте.

35. ТЕМА № 1 Основы воздушной навигации

36. Азимут (пеленг) ориентира.

37. Заданный путевой угол и линия заданного пути.

39. Линия пути и линия положения.

40. Ортодромия.

41. Ортодромия.

42. Основные свойства ортодромии.

43. Локсодромия

44. Локсодромия

45. Основные свойства локсодромии.

46. Линия равных азимутов.

47. Линии положения.

49. Географические координаты.

50. Географическая широта.

51. Географическая долгота.

52. ТЕМА № 1 Основы воздушной навигации

53. Системы координат применяемые в навигации.

54. Сферическая система координан

55. Сферическая широта.

56. Сферическая долгота.

57. Геодезическая система координат.

58. Ортодромическая система координат.

59. Общая ортодромическая система координат.

60. Общая ортодромическая система координат.

61. Частная ортодромическая система координат.

62. Прямоугольная система координат.

63. Полярная система координат.

64. Значение наклонной и горизонтальной дальностей

(PDF) Приближенные модели ортодромной навигации

Онлайн-калькулятор: Расстояние через Землю

Расстояние по Земле

Расстояние сквозь Землю

Расстояние по дуге большого круга | Тригонометрия: составные углы

Как найти формулу для расстояния по большому кругу?

Предварительные мероприятия

Координаты

Подход 3: сферическая тригонометрия

Зачем нужны гаверсины?

Geodesy: как рассчитать расстояние по прямой между двумя точками, которое представлено долготой и широтой? — Использование

Как разрабатывать функции с географией | Надим Кавва

Пример теории и науки о реальных данных

Две точки на сфере