Как рассчитать угловую скорость и радиус поворота?
0 +1 -1
flyman Админ. ответил 4 года назад
Ваша терминология немного запутана, но я собираюсь предположить, что вы спрашиваете, как рассчитать радиус поворота и скорость поворота на основе скорости и угла крена. Эти формулы можно найти в руководстве пилота FAA по Аэронавтическим знаниям, которое доступно бесплатно онлайн.
В справочнике приведены формулы скорости поворота и радиуса поворота на стр. 4-34:
R=V211.26tan⁡θ» role=»presentation»>R=V211.26tanθ
R=V211.26tanθ
ω=1,091tan⁡θV» role=»presentation»>ω = 1, 091 tan θ V
ω=1,091tanθV
Используемые переменные:
- V
» role=»presentation»>В
V= истинная скорость полета в узлах
- R
» role=»presentation»>Р
R= радиус поворота в футах
» role=»presentation»>θ
θ= угол крена в градусах
- ω
» role=»presentation»>ω
ω= скорость поворота в градусах в секунду
Например, на 120 узлах и угле крена 30°, радиус поворота и тариф поворота:
R=120211.
26tan⁡30=14,40011.26×0.5773=2,215feet≈13nautical mile» role=»presentation»>R = 120 2 11.26 tan 30 = 14 , 400 11.26 × 0.5773 = 2 , 215 f e e T ≈ 1 3 n A u T i c a l m i l e
R=120211.26tan30=14,40011.26×0.5773=2,215feet≈13nautical mile
ω=1,091tan⁡30120=1,091×0.5773tan⁡30120=5.25°/sec» role=»presentation»>ω = 1, 091 tan 30 120 = 1, 091 × 0.5773 tan 30 120 = 5.25 ° / s e c
ω=1,091tan30120=1,091×0.5773tan30120=5.25°/sec
«Магические константы» в этих формулах (11.26
» role=»presentation»>11.26
11.26
и 1,091
» role=»presentation»>1,091
1,091
) коэффициенты пересчета для задействованных единиц (узлы, ноги и степени). Физики использовали бы единичные формулы, включающие g
» role=»presentation»>г
g
, ускорение из-за силы тяжести (примерно 9.
8m/sec2
» role=»presentation»>9.8m/sec2
9.8m/sec2
).
Вы также можете переставить формулы выше, используя простую алгебру, чтобы выяснить требуемый угол банка, учитывая желаемую скорость поворота или радиус поворота.
Наконец, обратите внимание, что все становится намного сложнее, если вы учитываете ветры наверху . Скорость поворота всегда будет одинаковой независимо от ветра, но радиус поворота
Другие полезные ссылки:
- Руководство пилота по аэронавигационным знаниям (цитируется выше)
- Авиационный формуляр имеет раздел по поворотам
- Стандартная скорость поворота статьи в Википедии
- Статья Banked turn в Википедии
Есть также некоторые «связанные вопросы» в правой части этой страницы, которые могут быть полезны.
Автор ответа: TypeIA
0 +1 -1
flyman Админ. ответил 4 года назад
После всех этих ответов с имперскими единицами позвольте мне объяснить это с единицами Си, начиная с первых принципов. R-радиус, v-скорость полета, m-масса,g — гравитационная постоянная, Φ — угол крена и L-подъем.
Подъем должен быть равен весу (m·g) и центробежной силе (m·ω2·R = m·v2R
» role=»presentation»>v2R
v2R
), так
L=(m⋅g)2+(m⋅ω2⋅R)=ρ2⋅v2⋅cL⋅S» role=»presentation»>L = (m ⋅ g ) 2 + (m ω ω 2 ⋅ R ) − − − − − − − − − − − − − − − √ = ρ 2 ⋅ v 2 ⋅ c L ⋅ S
L=(m⋅g)2+(m⋅ω2⋅R)=ρ2⋅v2⋅cL⋅S
с ρ плотность воздуха, cL
» role=»presentation»>cL
коэффициент подъемной силы и S площадь поверхности крыла.
Теперь конвертируйте, чтобы вы получили v:
» role=»presentation»>v = (m ⋅ g ) 2 (ρ 2 ⋅ c L ⋅ S ) 2 — (m R ) 2 − − − − − − − − − − − − − − − √ 4
v=(m⋅g)2(ρ2⋅cL⋅S)2−(mR)24
Теперь вы можете видеть, что номинатор не может стать нулевым или меньше, что дает вам минимальный радиус для заданной скорости и максимального коэффициента подъема cLmax
» role=»presentation»>c L m A x
cLmax
:
R≥2⋅mρ2⋅cLmax⋅S,» role=»presentation»>R ≥ 2 ⋅ m ρ 2 ⋅ c L m A x ⋅ S,
R≥2⋅mρ2⋅cLmax⋅S,
и вообще:
R=2⋅mρ2⋅cL⋅S=vω=v2g⋅nz2−1 » role=»presentation»>R = 2 ⋅ m ρ 2 ⋅ c L ⋅ S = v ω = v 2 g ⋅ n 2 z− 1 − − − − − √R=2⋅mρ2⋅cL⋅S=vω=v2g⋅nz2−1
Это похоже на «радиусный барьер»: повороты не могут лететь плотнее, чем это.
Это происходит из-за увеличения центробежной силы, которая прибывает из более крутых поворотов полета. Чем круче поворот, тем быстрее вы должны лететь, чтобы создать достаточный подъем для компенсации веса и центробежной силы.
Что все еще увеличивается, так это ваша угловая скорость ω:
ω=vR=g⋅tanΦv=g⋅nz2−1v» role=»presentation»>ω = v R = g ⋅ t A n Φ v = g ⋅ n 2 z− 1 − − − − − √ v
ω=vR=g⋅tanΦv=g⋅nz2−1v
Внизу я построил планер. Вы можете ясно видеть радиус барьера на 40 м. Поверьте мне, это выглядит точно так же для авиалайнера, только цифры больше.
Если вам нужна быстрая формула для оценки радиуса, вам нужно использовать квадрат воздушной скорости, так что это не простая линейная зависимость. Для поворота с креном 30° (nz
» role=»presentation»>nz
nz
= 1.15), знаменатель уравнения радиуса составляет около 4, поэтому, чтобы вычислить радиус поворота в метрах, разделите квадрат воздушной скорости на 4 или возьмите квадрат половины вашей воздушной скорости в метрах в секунду.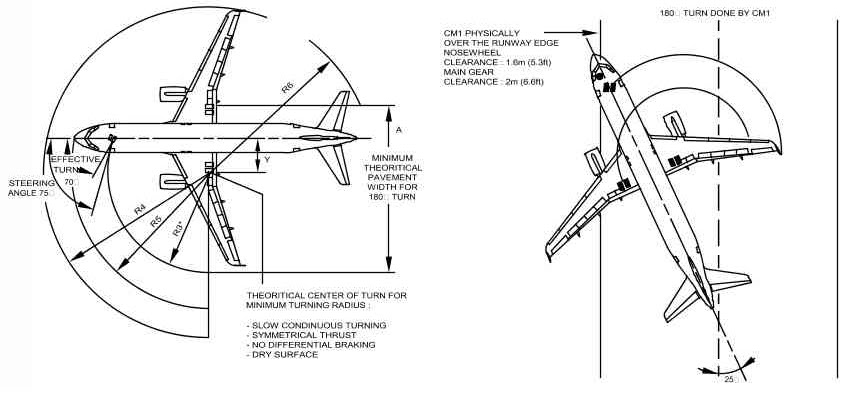
Для скорости поворота в градусах в секунду разделите 220 на скорость полета в метрах в секунду. Полет медленнее позволяет более высокую скорость поворота.
Теперь о другой крайности: гиперзвуковым самолетам нужно много места для маневрирования. У меня есть здесь некоторые ценности, просто для удовольствия:
Высокая скорость делает это почти терпимым, в конце концов, половина оборота на Mach 6 и 2 g занимает всего 336 секунд, то есть менее 6 минут. Авиалайнеры крен только 30° или меньше, поэтому первая колонка действительна, если вы летите ваш гиперзвуковой автомобиль, как авиалайнер.
Автор ответа: Peter Kämpf
0 +1 -1
flyman Админ. ответил 4 года назад
Если вы собираетесь делать это в кокпите, хорошее эмпирическое правило поможет больше, чем точная формула:
Угол крена для тарифа 1 оборот speed10+7
» role=»presentation»>speed10+7
speed10+7.
и
Диаметр поворота составляет 1% от скорости.
например. для поворота 120кц вам 12010+7=19°
» role=»presentation»>12010+7=19°
12010+7=19°
банка и имеют 120100=1.2
» role=»presentation»>120100=1.2
120100=1.2
диаметр поворота Нм
Автор ответа: Radu094
0 +1 -1
flyman Админ. ответил 4 года назад
Другой подход заключается в том, чтобы просто отметить, что в любом повороте уровня связь между общим самолетом G (GT
» role=»presentation»>GT
GT
), радиальный G (GR
» role=»presentation»>GR
GR
), и Божья G должна соответствовать Пифагору.
так
GT2=GR2+1
» role=»presentation»>G2T=G2R+1
GT2=GR2+1
или,
GR=GT2−1
» role=»presentation»>G R = G 2 T− 1 − − − − − − √
GR=GT2−1
а так как радиус поворота равен квадрату скорости над радиальным G,
R=V2GT2−1» role=»presentation»>R = V 2 G 2 T− 1 − − − − − − √
R=V2GT2−1
общий самолет G, конечно, это просто лифт, разделенный на вес самолета.
и если мы находимся ниже скорости маневрирования (самая низкая скорость полета, при которой мы можем генерировать коэффициент нагрузки G-Limit) и поворачиваемся на максимальный угол атаки (AOA), то подъем самолета CLmaxpV2S
» role=»presentation»>C L m A x p V 2 S
CLmaxpV2S
и вес, конечно, может быть представлен подъемом произведенным на АТ CLmax
» role=»presentation»>C L m A x
CLmax
когда на скорости стойла или CLmaxpVs2S
» role=»presentation»>C L m A x p V 2 S S
CLmaxpVs2S
.
Так что всего самолетов G, (GT
» role=»presentation»>GT
GT
), который просто поднимает разделенный весом, можно представить как CLmaxpV2SCLmaxpVs2S
» role=»presentation»>C L m A x p V 2 S C L m A x p V 2 S
CLmaxpV2SCLmaxpVs2S
или V2VS2
» role=»presentation»>V2V2S
V2VS2
Подставляя в Формулу радиуса поворота, мы получаем формулу радиуса поворота для поворота максимальной производительности уровня (ниже скорости маневрирования), выраженную как функция истинной воздушной скорости самолета и скорости сваливания самолета (в True):
R=V2Vs2g(V4−Vs4)» role=»presentation»>R = V 2 V 2 s g ( V 4—V 4 s− − − − − − − √)
R=V2Vs2g(V4−Vs4)
где:
- R
» role=»presentation»>Р
R….
Радиус разворота - V
» role=»presentation»>В
V…. Самолет истинная скорость воздуха
- VS
» role=»presentation»>VS
VS… Скорость стойла (TAS)
- g
» role=»presentation»>г
g…. 32.2 ft/sec2
» role=»presentation»>f T / s e c 2
ft/sec2(необходимо конвертировать из единиц измерения Earth-G в ft/sec2
» role=»presentation»>f T / s e c 2
ft/sec2
Радиус разворотаГрафик, он выглядит так, как показано ниже: это для самолета со скоростью сваливания 58 kt (правда) и плакатом G-limit 3,8 Gs. (Излом при 122 КТ происходит из-за того, что, как только мы быстрее маневрируем, мы ограничены плакатом G и больше не можем достичь CLmax
» role=»presentation»>C L m A x
CLmax
без разрушения или перенапряжения планера.)
Автор ответа: Чарльз Бретана
Радиус поворота Калькулятор | Вычислить Радиус поворота
✖Скорость является векторной величиной (она имеет как величину, так и направление) и представляет собой скорость изменения положения объекта во времени. | Сантиметр в часСантиметр в минутуСантиметр в секундуКосмическая скорость прежде всегоКосмическая скорость СекундаКосмическая скорость третьяСкорость ЗемлиФут в часФут в минутуФут в секундуКилометры / часКилометр в минутуКилометры / секМорской узелУзел (Великобритания)МахаМаха (стандарт СИ)Метр в часМетр в минутуметр в секундумили / часмили / минутумили / секМиллиметр в деньМиллиметр / часМиллиметр в минутуМиллиметр / секМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20 ° C и 10 метров глубиной)Двор / часДвор / минутуДвор / сек | +10% -10% | |
✖Коэффициент нагрузки — это отношение аэродинамической силы самолета к его полной массе.ⓘ Коэффициент нагрузки [n] | +10% -10% |
ⓘ Скорость [v]|
✖Радиус поворота — это радиус траектории полета, по которой самолет поворачивает по круговой траектории. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
ⓘ Радиус поворота [R]
👎
Формула
сбросить
👍
Радиус поворота Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
2)-1))
Каковы четыре основных летных маневра?
Самолет вращается по крену, тангажу и рысканью, а также движется в горизонтальном, вертикальном и поперечном направлении. Четыре основных принципа (полет по прямой и горизонтальный, повороты, набор высоты и снижение) — это основные маневры, которые управляют самолетом с помощью шести движений полета.
Share
Copied!
аэродинамика — Действительно ли радиус поворота при фиксированном угле крена не зависит от типа самолета?
Задавать вопрос
спросил
Изменено 2 года, 5 месяцев назад
Просмотрено 544 раза 92}{g \tan(b)} $$
Где $R$ — радиус поворота, $v$ — скорость, $g$ — ускорение свободного падения и $b$ — угол крена.
Эта формула разбросана по всему Интернету (с вариациями в зависимости от используемых единиц измерения). Примеры приведены здесь и здесь.
У меня вопрос, почему в формуле нет ссылки на физические характеристики самолета? Действительно ли взаимосвязь между радиусом поворота и углом крена не имеет ничего общего с весом самолета, размахом крыла или конструкцией аэродинамического профиля? Действительно ли одна и та же формула верна как для планера (планера), так и для большого пассажирского самолета?
Надеюсь на объяснение без математики, пожалуйста!
- аэродинамика
- авиафизика
$\endgroup$
2
$\begingroup$
Если поворот полностью скоординирован, радиус поворота при заданном угле крена будет зависеть от скорости самолета и местного значения силы тяжести.
Это из-за простого вектора и геометрии: вертикальная составляющая подъемной силы все равно должна выдерживать вес самолета (будь то дельтаплан или АН-225, Helio Courier на краю сваливания или SR-71) , но горизонтальная составляющая, создаваемая креном, создает горизонтальное (=> центростремительное) ускорение, которое фиксировано по отношению к силе тяжести для данного угла крена.
Проблема в том, что это центростремительное ускорение определяется как радиусом поворота , так и скоростью . Таким образом, если ваш дельтаплан и ваш SR-71 хотят сделать разворот с одинаковым радиусом (в пределах их обычного диапазона полета), они сделают это с совершенно разными углами крена.
$\endgroup$
10
$\begingroup$
Почему в формуле нет ссылки на физические характеристики самолета?
В горизонтальном установившемся полете Вес = Общая подъемная сила = Вертикальная подъемная сила. Отношение 90 059 90 060 общей подъемной силы к вертикальной подъемной силе = 1. В насыпи необходимо создать большую подъемную силу, чтобы поддерживать достаточную вертикальную подъемную силу. Отношение вертикальной подъемной силы к горизонтальной подъемной силе равно касательной (угол крена).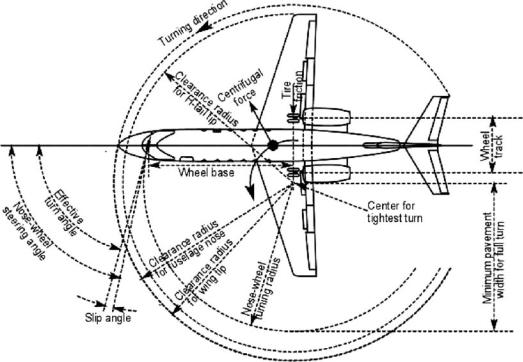
Компонент горизонтальной подъемной силы изменяет направление траектории полета. Сила , перемещающая его в новом направлении, равна массе, умноженной на ускорение. Это всегда пропорционально подъемная сила независимо от веса.
Поскольку боковое движение ускоряется от нуля, а направление всегда меняется, боковое сопротивление самолета не столь значительно, как боковое ускорение по сравнению с энергией движения вперед.
Здесь «физические характеристики самолета» учитываются в скорости: планер имеет гораздо меньший радиус поворота, чем реактивный авиалайнер, из-за гораздо более низкой скорости сваливания . Здесь в игру вступают тип аэродинамического профиля и нагрузка на крыло. 92$/мг (угол тангенса крена)
Теперь мы можем ясно видеть, что энергия объекта пропорциональна квадрату скорости. Вес (поэтому подъемная сила) составляет мг. Человек просто получает меньшую скорость поворота с
более быстро движущийся объект для заданной величины бокового ускорения .
Теперь, если вы отключите питание и захотите повернуть, физические характеристики самолета будут иметь значение. Широкие, с низким удлинением, тянущиеся крылья делают бипланы более маневренными в поворотах, чем их более быстрые аналоги-монопланы. Это одна из причин, по которой трипланы были в моде до того, как была разработана новая тактика.
$\endgroup$
Что такое радиус поворота (авиация)?
Понимание радиуса поворота имеет решающее значение для безопасной эксплуатации самолета пилотом.
Радиус разворота (или радиус разворота) — это горизонтальное расстояние, необходимое для разворота самолета. Она изменяется в зависимости от угла крена и квадрата истинной воздушной скорости. Радиус поворота измеряется от центра поворота до самолета.
Диаметр разворота — это горизонтальное расстояние, необходимое для разворота самолета, измеренное от одной стороны круга разворота до другой.
Радиус и диаметр нестандартного разворота зависят от угла крена, скорости разворота и воздушной скорости. Радиус поворота увеличивается по мере увеличения скорости полета. Когда и угол крена, и скорость поворота увеличиваются, радиус поворота уменьшается.
В этой статье мы углубимся в механику расчета радиуса поворота со стандартной и нестандартной скоростью, дав вам четкое представление об этой жизненно важной концепции.
Радиус поворота Объяснение
Первое, что вам нужно знать, это то, насколько круто вы поворачиваете (т. е. радиус поворота) зависит как от скорости поворота, так и от вашей воздушной скорости. Кроме того, скорость разворота также определяется углом крена и воздушной скоростью.
Не становитесь жертвой путаницы между скоростью поворота и радиусом поворота:
- Скорость поворота : Как быстро меняется ваш курс.
- Радиус поворота : Насколько сильно вы поворачиваетесь (насколько мал ваш радиус поворота).
При увеличении скорости полета радиус поворота увеличивается. При увеличении скорости поворота радиус поворота уменьшается.
Другими словами:
- Увеличение воздушной скорости -> Увеличение радиуса поворота (больше радиус поворота)
- Увеличение скорости поворота -> уменьшение радиуса поворота (меньший радиус поворота)
Взгляните на пример из Главы 5 (5-41) Справочника пилотов по авиационным знаниям (PHAK):
Самолет, летящий со скоростью 120 узлов, угол крена 30 градусов.
Самолет, летящий со скоростью 140 узлов, угол крена 30 градусов.
Два самолета по ошибке влетели в каньон. Каньон имеет ширину 5000 футов и имеет высокие стены с каждой стороны. Пилот на верхнем фото летит со скоростью 120 узлов. Пилот на нижнем фото летит со скоростью 140 узлов.
После того, как пилоты осознали свою ошибку, они быстро развернули самолет и изменили курс, используя угол крена 30 градусов.
На верхнем фото этот разворот на 30° требовал радиуса около 4000 футов, чтобы завершить изменение направления на 180° и безопасно вывести пилота из каньона.
Самолет на нижнем изображении летит со скоростью 140 узлов и использует угол крена 30° для изменения курса. Хотя он летит всего на 20 узлов быстрее, чем самолет на верхнем изображении, для безопасного изменения курса ему требуется радиус поворота более 6000 футов. К сожалению, самолет врежется в стену каньона, потому что ее ширина составляет всего 5000 футов.
Другими словами, скорость оказывает большее влияние на то, сколько места требуется для поворота, чем что-либо еще. К сожалению, многие пилоты по ошибке увеличили угол крена вместо того, чтобы снизить скорость, столкнувшись с таким сценарием.
Влияние ветра
Ветер также играет решающую роль в окончательном радиусе разворота самолета относительно земли.
Без ветра пилот может выполнить наземный разворот с постоянным радиусом, сохраняя одинаковый угол крена на всем протяжении; однако при любом ветре трудности выполнения такого маневра возрастают.
Любая составляющая ветра создаст искаженный круг разворота относительно земли, если сохраняется постоянный угол крена.
Следовательно, при выполнении разворотов на земле при наличии ветра пилоты должны учитывать снос, соответствующим образом изменяя угол крена.
Если пилот не выполняет развороты относительно земли (или навигационного средства, физического или виртуального), пилоту не нужно изменять угол крена на протяжении всего разворота.
Стандартный радиус поворота скорости (норма один оборот)
Разворот со стандартной скоростью (также известный как разворот с одной скоростью) — это разворот, при котором воздушное судно меняет курс на 360 градусов со скоростью 3 градуса в секунду (всего 2 минуты).
Хотя угол крена стандартных разворотов колеблется в зависимости от воздушной скорости, разворот всегда занимает две минуты, потому что вы изменяете угол крена, чтобы поддерживать скорость разворота .
Следовательно, чем выше ваша скорость полета, тем больше будет радиус разворота, а чем меньше ваша скорость полета, тем меньше будет круг разворота, время останется 2 минуты, но угол крена будет разным для разных скоростей полета.
С другой стороны, нестандартные повороты могут иметь любую скорость поворота, поэтому расчет радиуса более сложен.
Диаметр стандартного поворота обычно составляет около 1% от вашей скорости относительно земли. Радиус равен половине этого диаметра. Например, если вы летите со стандартной скоростью разворота на скорости 100 узлов, ваш разворот будет иметь диаметр примерно одну морскую милю и радиус 0,5 морской мили.
Как рассчитать угол крена для стандартного поворота на один оборот
Чтобы рассчитать приблизительный угол крена, необходимый для стандартного поворота, разделите истинную воздушную скорость (TAS) на 10 и прибавьте 7.
Например, самолету, летящему со скоростью 120 узлов TAS, потребуется угол крена 19 градусов для стандартного поворота:
- 120 TAS / 10 = 12
- 12 + 7 = 19 градусов
Почему важен радиус поворота?
При полете важно понимать радиус поворота. Понимание факторов, влияющих на радиус поворота, может помочь вам планировать и избегать препятствий во время полета, держать вас в воздушном пространстве, соответствующем вашей высоте, и многое другое.